Вопрос9) определение. Ранг матрицы а - максимальный порядок неравного нулю минора (минор - определитель квадратной матрицы ). Обозначается

Ранг матрицы – это наивысший порядок минора матрицы, отличного от нуля.

Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

Элементарными преобразованиями строк называют:

• перестановка местами любых двух строк матрицы;

• умножение любой строки матрицы на константу  ,  ;

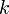• прибавление к любой строке матрицы другой строки.

Аналогично определяются элементарные преобразования столбцов.

Вопрос10) Определение. Минор, определяющий ранг матрицы, называется Базисным минором. Строки и столбцы, формирующие бм, назвыаются базисными строками и столбцами.

• Теорема (о базисном миноре): Пусть 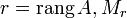  — базисный минор матрицы  , тогда:

  1. базисные строки и базисные столбцы линейно независимы;

  2. любая строка (столбец) матрицы   есть линейная комбинация базисных строк (столбцов).

Вопрос11) Теорема Кронекера-Капелли

— критерий совместности системы линейных алгебраических уравнений.

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.  Теорема Кронекера-Капелли применяется при исследованиях систем алгебраических уравнений (без непосредственного решения системы). В результате исследования должна быть записана эквивалентная система алгебраических уравнений с минимальным числом уравнений.

Вопрос12) Чтобы решить систему линейных алгебраических уравнений общего вида, сначала выясняем ее совместность, используя теорему Кронекера – Капелли. Если ранг основной матрицы не равен рангу расширенной матрицы, то делаем вывод о несовместности системы.

Если ранг основной матрицы равен рангу расширенной матрицы, то выбираем базисный минор и отбрасываем уравнения системы, которые не участвуют в образовании выбранного базисного минора.

Если порядок базисного минора равен числу неизвестных переменных, то СЛАУ имеет единственное решение, которое находим любым известным нам методом.

Если порядок базисного минора меньше числа неизвестных переменных, то в левой части уравнений системы оставляем слагаемые с основными неизвестными переменными, остальные слагаемые переносим в правые части и придаем свободным неизвестным переменным произвольные значения. Из полученной системы линейных уравнений находим основные неизвестные переменные методом Крамера, матричным методом или методом Гаусса.