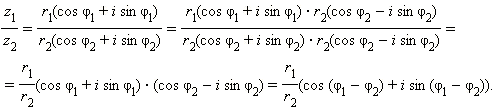Вопрос1) Пару Действительных чисел Называют упорядоченной, если указа

Но, какое из них считается первым, какое - вторым. Примеры упорядоченных пар: Отметим, что последние две пары различны, хотя и об

Разованы одними и теми же числами.

Каждую упорядоченную пару чисел обозначим одной буквой, введем понятие равенства двух пар, определим действия над ними. Рассмотрим две упорядоченные пары

Эти лары называют равными, если Т. е.

Суммой двух пар (7.1) называют упорядоченную пару   а их произведением — упорядоченную пару

Из соотношения (7.3) видно, что пара

(7.5)

Обладает тем свойством, что сложение ее с любой другой упорядоченной парой не меняет исходной парЫ: . Пара (715) играет роль нуля при

Сложении упорядоченных пар; назовем ее нуль-парой.

Разностью . двух упорядоченных пар (7.1) называют такую упорядоченную пару

Вычитание упорядоченных пар (7.1) определяется следующим образом:

(7.6)

Частным , где Двух упорядоченных пар (7.1) называют такую упо

Рядоченную пару

Если То частное Двух упорядоченных-пар (7.1)

(7.7)

Из этой формулы следует, что если То

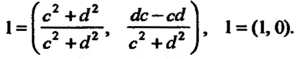
Вопрос2) Комплексным числом   называется число вида  , где   и   – действительные числа,   – так называемая мнимая единица. Число   называется действительной частью ( )комплексного числа  , число   называется мнимой частью ( ) комплексного числа  .

 – это ЕДИНОЕ  ЧИСЛО, а не сложение.

С алгебраической формой комплексного числа мы уже познакомились,   – это и есть алгебраическая форма комплексного числа

Вопрос3) Полярная система координат — двухмерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.

Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается  ) соответствует расстоянию от точки до начала координат. Угловая координата, также называется полярным углом или азимутом и обозначается  , равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.

Вопрос4) Арифметические действия над комплексными числами, записанными в тригонометрической форме, производятся следующим образом. Пусть z₁ = r₁(cos φ₁ + i sin φ₁) и z₂ = r₂(cos φ₂ + i sin φ₂). Имеем: 

Видно, что в тригонометрической форме операции умножения и деления производятся особенно просто: для того, чтобы перемножить (разделить) два комплексных числа, нужно перемножить (разделить) их модули и сложить (вычесть) их аргументы.

Отсюда следует, что для того чтобы перемножить n комплексных чисел, нужно перемножить их модули и сложить аргументы: если φ₁, φ₂, ..., φ_n – аргументы чисел z₁, z₂, ..., z_n, то 

В частности, если все эти числа равны между собой, то получим формулу, позволяющую возводить комплексное число в любую натуральную степень.

Первая формула Муавра: