Продолжение второй лекции

Логические операции с понятиями. В математике исследуются различные операции, выполняемые над числами: их можно складывать, делить, вычитать, умножать и т.п. Точно также и в логике исследуются различные операции над понятиями. Причем операции над понятиями бывают двух видов: операции с объемами понятий и операции с их содержанием.

Объем понятия можно графически представить в виде кругов Эйлера (рис. 2.1). Каждая точка такого круга представляет собой элемент объема понятий.

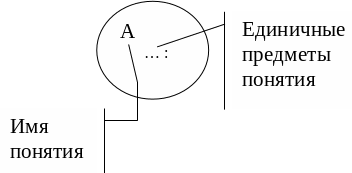
Рис. 2.1. Круги Эйлера

Пусть даны произвольные два понятия А и В. Будем говорить, что эти два понятия несравнимы, если при их определении используются понятия род. Род первого понятия отличен от рода второго понятия. Например, при обычной формулировке понятий несравнимыми будут понятия "человек" и "чайник" (рис. 2.2, б).

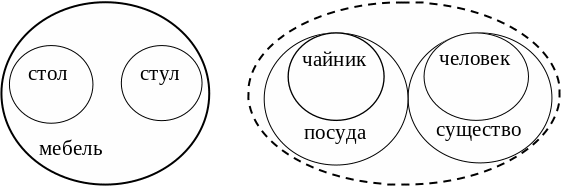
a) б)

Рис. 2.2. Сравнимые и несравнимые понятия

В их определении используются два различных понятия: для понятия "человек" – "существо", а для понятия "чайник" – "посуда", то есть у каждого из этих понятий имеется свой род, отличный от других понятий. Понятия называются сравнимыми, если при их определении используется общее родовое понятие. Например, пара понятий "стол – стул" будут являться сравнимыми, поскольку при их определении используется одно и тоже понятие – "мебель" (рис.2.2, а).

В логических отношениях могут находиться только сравнимые понятия. Два понятия называются совместимыми, если и только если пересечение их объемов не пустое. Это означает, что в универсуме имеется, по крайней мере, один объект, существенные признаки которого относятся как к одному понятию, так и к другому. В противном случае, понятия являются несовместимыми.

Существуют три вида отношений совместимости – равнообъемность (равнозначности), пересечение, подчинение; и три вида отношений несовместимости – противоречие, противоположность, соподчинение. Они представлены соответственно на рис. 2.3.

1. 2. 3.

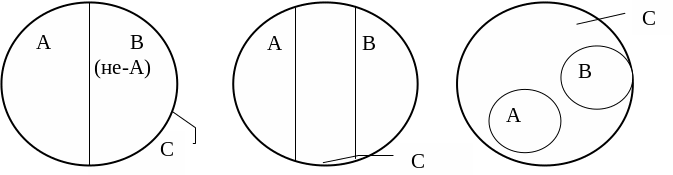
4. 5. 6.

Рис. 2.3. Отношения между совместимыми (1, 2, 3) и несовместимыми (4, 5, 6) понятиями

1. Равнообъемность – в подобном отношении находятся понятия, объемы которых совпадают полностью, хотя их содержание может в той или иной степени отличаться. Равнозначные понятия нередко используются в юридической практике. Таковы, например, понятия "гражданство" и "подданство". В государствах с республиканской формой правления, где есть конституция, употребляется понятие "гражданство", а при монархической форме правления ему соответствует "подданство".

2. Подчинение – в таком отношении находятся понятия, из которых одно входит в объем другого, но не исчерпывает его, а составляет лишь часть. Более общее называется подчиняющим, а менее общее – подчиненным. Таковы, например, понятия "береза" и "дерево". Из двух общих понятий более общее иначе называется родом, а менее общее – видом. Поэтому отношение между ними именуется также отношением рода и вида или родовидовым отношением.

3. Пересечение – это отношение существует между понятиями, объемы которых совмещаются лишь частично. Например, понятия "россияне" и "русские" – перекрещивающиеся. Это значит, что не все россияне – русские, поскольку в России живут еще другие народы, например, украинцы. В то же время не все русские – россияне, так как некоторые русские живут за пределами России.

4. Противоречие – это отношение существует между понятиями, из которых одно отражает наличие у предметов каких-либо признаков, а другое – их отсутствие, то есть отношение между положительными и отрицательными понятиями. Важнейшие особенности взаимоотношений противоречащих понятий: исключая друг друга по содержанию в рамках общего для них рода, они по объему полностью исчерпывают объем родового понятия. Такими, например, выступают отношения между понятиями "металл" и "неметалл" в химии, "живое" и "неживое" в биологии, "производственная сфера" и "непроизводственная сфера" в экономических науках, "правовые отношения" и "неправовые отношения" в юридической области. Нетрудно заметить, что область В (не-А) расплывчата, неопределенна. Она охватывает самые разные предметы, объединенные только по одному признаку – отсутствию существенного признака.

5. Противоположность – в данных отношениях находятся понятия, каждое из которых выражает наличие у предметов каких-либо признаков, но сами эти признаки носят противоположный характер. Важнейшее отличие отношений между противоположными понятиями сводится к тому, что, будучи взаимоисключающими по содержанию, они могут не исчерпывать объема родового понятия. Противоположные понятия А и В занимают лишь крайние позиции в рамках общего для них рода и не исключают чего-то среднего. Много таких понятий имеется в арсенале юристов, например, "истец" – "ответчик".

6. Соподчинение – данное отношение характеризует понятия, которые имеют общий род и, взятые в отдельности, подчинены ему как виды, а вместе – соподчинены и, следовательно, обладают одной и той же степенью общности. Например, понятия "хвойные деревья" и "лиственные деревья"– виды родового понятия "деревья", находящиеся на одной ступени обобщения; следовательно, это соподчиненные понятия. Количество соподчиненных понятий не ограничивается двумя понятиями.

Для определения отношений между понятиями целесообразно воспользоваться приведенным ниже алгоритмом (рис. 2.4).

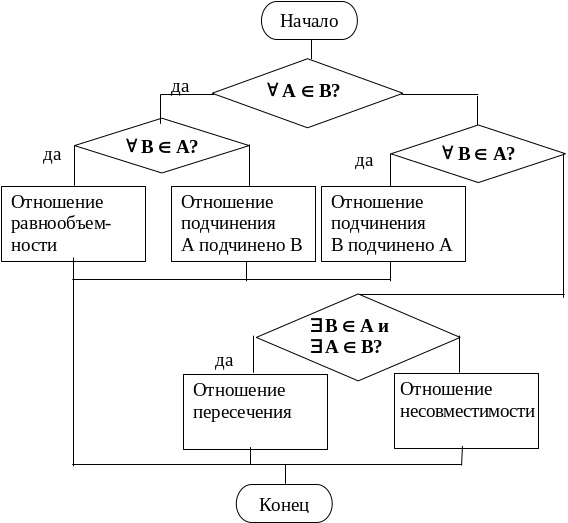
Рис. 2.4. Алгоритм определения отношений между понятиями: " – все, каждый; $ – некоторый; Î – принадлежит

Задание 3. Определить, в каком отношении между собой находятся следующие понятия. Изобразить их в виде круговых схем.

число, которое делится на "2" – A;

число, которое делится на "3" – В;

число, которое делится на "12" – С.

Решение.

1. Определим отношения между понятиями А и В. С этой целью задаем вопрос "Все ли числа, которые делятся на “2” (А) являются числами, которые делятся и на “3” (В)?". Ответ на это вопрос – нет. Далее, "Все числа, которые делятся на “3” (В), делятся на “2” (А)? ". Ответ – нет. Но на вопрос "Существуют ли числа, которые делятся на “2” (А) и на “3” (В) одновременно?" ответ будет "да". Таким образом, понятия А и В находятся в отношении пересечения (рис. 2.5, а).

2. Определим отношения между понятиями А и С. Между этими понятиями имеем отношения подчинения. При этом понятие А является родовым, а понятие С – видовым (рис. 2.5, б).

3. Определим отношения между понятиями В и С. Между этими понятиями имеем аналогичные предыдущему случаю отношения подчинения, при которых понятие В выступает как родовое, а понятие С – как видовое (рис. 2.5, в).

4. Строим результирующую схему отношений между понятиями.

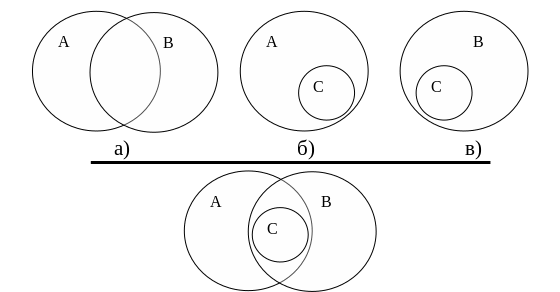
Рис. 2.5. Графическое решение задачи

Задание 4. Подберите понятия, отношения между которыми соответствовали бы нижеприведенной круговой схеме.

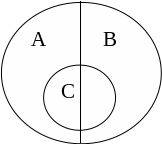
Решение.

1. Отношения между понятиями А и В – отношения противоречия. В таких отношениях находятся понятия "мужчина" (А) и "женщина" (В).

2. Отношения между понятиями А и С - отношения пересечения. В таких отношениях находятся понятия "мужчина" (А) и "студент" (С).

3. Отношения между понятиями В и С – отношения пересечения. В таких отношениях находятся понятия "женщина" (В) и "студент" (С).

4. Таким образом, получаем следующие понятия А – "мужчина", В – "женщина", С – "студент".

Ограничение и обобщение понятий. Ограничить непустое понятие – это указать такое непустое понятие, объем которого будет полностью входить в объем исходного понятия. Реализация данной логической операции осуществляется при переходе от родового понятия к видовому путем добавления к содержанию данного родового понятия видообразующих признаков.

Например, пусть на множестве животных задано понятие "слон". Тогда переход к понятию "индийский слон" является процедурой ограничения. Понятие "индийский слон" является видовым по отношению к понятию "слон", которое считается родовым.

Процесс ограничения можно продолжить, образовав еще одно понятие, которое является видовым по отношению к понятию "индийский слон". Таковым, например, будет являться понятие "индийский слон из московского зоопарка". Над этим понятием, в свою очередь, можно провести операцию ограничения. В результате такой процедуры возникает система подчиненных друг другу понятий (рис. 2.6). Для непустых понятий пределом их ограничения считается единичное понятие.

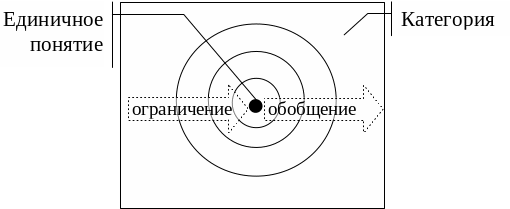
Рис. 2.6. Графическое отображение операций ограничений и обобщений понятий

Операцию ограничения объема нельзя путать с делением, членением объекта на части. Ограничение понятия – это логическая операция с его объемом, в то время как деление целого на части осуществляется с самими предметами. Например, ограничением понятия "завод" будет являться понятие с меньшим объемом – "механический завод". Но при делении объекта на части осуществляется переход от данного понятия к таким понятиям, как "механический цех", "заводоуправление" и т.п. С логической точки зрения, различие между двумя этими процедурами состоит в том, что при правильном ограничении исходного понятия B до понятия A должно оказаться истинным предложение "Всякий A есть B", в то время как при членении предмета B до предмета A предложение указанного вида будет ложным. В самом деле, истинным является предложение "Всякий механический завод есть завод", но ложным будет предложение "Всякий механический цех есть завод".

Обобщить понятие – это указать такое понятие, объем которого полностью поглощает объем исходного понятия. Реализовать данную операцию возможно, если осуществить переход от видового к родовому понятию путем отбрасывания от содержания данного родового понятия видообразующих признаков.

Так, например, результатом обобщения понятия "газета" будет являться понятие "печатное периодическое издание". Последнее понятие также можно обобщить до понятия, скажем, "печатная продукция". В результате последовательного выполнения этой процедуры возникает система подчиненных друг другу понятий (см. рис. 2.6).

Пределом обобщения понятий является универсальное понятие (категория). Категория – это предельно общие, фундаментальные понятия. К ним относятся: материя, движение, пространство, время, сознание, истина, содержание, форма, количество, качество, необходимость, случайность, причина и следствие и целый ряд других философских понятий.

Задание 5. Правильно ли произведены обобщения понятий:

маленькая овца – овца – отара.

Решение.

В данном случае обобщение понятий произведено неверно. Ошибка совершена при переходе от понятия "овца" к понятию "отара" ("стадо овец"), поскольку объемы этих понятий не находятся в отношении подчинения.

Задание 6. Правильно ли произведены ограничения понятий:

сын – отец – дед.

Решение.

Ограничение понятий произведено верно. В данном случае переход от понятия "сын" к понятию "отец", и далее – от понятия "отец" к понятию "дед" представляет собой переход от родового понятия к видовому путем добавления к содержанию данного родового понятия видообразующих признаков.

Определение. В самом широком смысле определение есть логическая операция, позволяющая, во-первых, отыскивать, отличать, выделять интересующие нас предметы по их внешним признакам и, во-вторых, уточнять, раскрывать значение вводимых в научный оборот терминов (выражений) через известные термины. В основе логической операции определения понятий лежит закон тождества. Определить понятие – это указать предел, границу его объема и тем самым раскрыть содержание посредством другого понятия, величина (предел, граница) объема и содержание которого известны.

Структура определения имеет форму тождества: DFD = DFD, где "DFD" – определяемое понятие (дефиниендум), "DFN" – определяющее понятие (дефиниенс). Эту формулу следует знать, ибо она составляет основу всей логической операции определения понятий.

Выделяют разные виды и типы определения. Различают номинальные и реальные определения. При этом следует различать семантически и прагматически реальные и номинальные определения.

С семантической точки зрения, определение считается реальным, если значением определяемого термина является реально (материально) существующий предмет или его характеристики (свойства, отношения, предметно-функциональные характеристики), а номинальными (от лат. "nоmеn" – название, имя) – если значением определяемых терминов являются предметы, реально (материально) не существующие, а также их характеристики. К номинальным в этом смысле будут относиться определения таких терминов, как, например, "кентавр", "единорог", "квадратный круг" и т.п. К числу номинальных следует отнести и определения математических терминов, а также различного рода абстрактные и идеальные объекты естественных наук – "число", "идеальный газ", "абсолютно черное тело" и т.д.

С прагматической точки зрения, номинальные и реальные определения различают по характеру целей и намерений, которые имелись в виду при формулировке определений. Если цель введения определения заключается в как можно более точном разъяснении содержания некоторого общеупотребимого термина, то говорят, что определение является реальным. В этом случае иногда даже настаивают, что термин надо употреблять именно в таком, а не ином смысле. Таким образом, реальное определение – это высказывание о том, какой смысл будет заключен в понятии. Например, такое определение: "Жизнь есть способ существования белковых тел" (Ф.Энгельс). Если же указанной цели не ставится, а введением определения пытаются просто зафиксировать некоторую терминологию (возможно лишь на данный момент ее использования), то определение считается номинальным. В данном случае номинальное определение – это соглашение о том, как будет употребляться термин, при этом иногда даже специально подчеркивают условный характер определений посредством введения их такими фразами: "давайте считать, что термин А обозначает...", "термином А будем называть...", "под термином А будем понимать..." и т.д.

Кроме того, определения делятся на явные и неявные. Также существуют определенные приемы, которые сходны с определением и в некоторых случаях используются вместо него (табл. 2.2).

Таблица 2.2