
- •1. Введение в надежность
- •2. Надежность технических элементов
- •2.1. Основные понятия и определения
- •2.2. Функциональные показатели надежности элемента
- •Функция ненадежности элемента
- •2.3. Числовые показатели надежности
- •2.4. Основные законы распределения наработки до отказа
- •Распределение Вейбулла
- •Экспоненциальное распределение
- •Распределение Релея
- •Нормальное распределение
- •Усеченное нормальное распределение
- •Суперпозиции экспоненциальных распределений
- •2.5. Ремонтопригодность технических элементов
- •Функциональные показатели ремонтопригодности
- •Числовые показатели ремонтопригодности
- •Экспоненциальное распределение вероятности восстановления
- •Комплексные показатели ремонтопригодности
- •2.6. Определение показателей надежности элементов по результатам испытаний
- •Определительные испытания
- •Контрольные испытания
- •Лабораторные испытания элементов
- •3. Надежность технических систем
- •3.1. Надежность простых технических систем
- •3.2. Расчет надежности локальных технических систем
- •3.3. Надежностный синтез технических систем
- •4. Надежность программного обеспечения
- •4.1. Общие сведения о программном обеспечении
- •Жизненный цикл программного обеспечения
- •4.2. Показатели надежности программы и программного обеспечения
- •Понятие ошибки программы
- •Модель ошибки сертифицированного по
- •Модели поведения ошибок функционирующего по
- •Функциональные и числовые характеристики надежности по
- •4.3. Повышение надежности программного обеспечения
- •Повышение надежности по путем резервирования
- •Программное резервирование по предусматривает наличие двух (или более) алгоритмов , решения одной и той же задачи с одинаковыми исходными данными и двух по1 и по2 (рис. 4.13).
- •5. Литература
2.6. Определение показателей надежности элементов по результатам испытаний
Статистические
распределения
![]() и оценки параметров
и оценки параметров
![]() определяют только по результатам
испытаний элементов на надежность и
ремонтопригодность. По целевому
назначению подобные испытания подразделяют
на определительные и контрольные, по
месту проведения эксперимента – на
лабораторные и эксплуатационные.
определяют только по результатам
испытаний элементов на надежность и
ремонтопригодность. По целевому
назначению подобные испытания подразделяют
на определительные и контрольные, по
месту проведения эксперимента – на
лабораторные и эксплуатационные.
Определительные испытания
Цель этих
испытаний заключается в получении
первичных показателей надежности
![]() для вновь разработанных или модернизированных
элементов с неизвестными или слабо
изученными характеристиками. Одновременно
с этим выявляют типичные причины отказов
элементов и способы их устранения.
для вновь разработанных или модернизированных
элементов с неизвестными или слабо
изученными характеристиками. Одновременно
с этим выявляют типичные причины отказов
элементов и способы их устранения.
Определительные испытания чаще всего проводят в лабораторных условиях, реже – в условиях эксплуатации (см. ниже). Основными этапами
определительных испытаний являются выбор плана экспериментов и математическая (статистическая) обработка полученных данных.
План проведения экспериментов предусматривает выбор числа N испытуемых элементов, режима их работы (с заменой отказавших или без восстановления), условия окончания испытаний (длительность эксперимента ТЭ). Существует ряд типовых планов испытаний на надежность, обозначаемых тремя буквами: N – число испытуемых элементов; R или V – наличие или отсутствие восстановлений элементов при t0, ТЭ; ТЭ или r – условие окончания опытов.
Так, планом NVТЭ предусмотрено испытание N элементов без их восстановления, эксперимент заканчивается в заданный момент времени ТЭ.
План NVr соответствует испытанию N элементов без восстановления, но эксперимент заканчивается после отказа r элементов, r N.
При r = N получаем план NVN , предусматривающий окончание экспериментов после отказа всех N испытуемых элементов.
План NRТЭ предполагает испытание N элементов с заменой отказавших и завершение эксперимента в заданный момент времени ТЭ.
Наконец, план NRr ориентирован на испытание N элементов с заменой отказавших и окончанием опытов после отказа r, r < N элементов.
Во всех
рассмотренных планах главной задачей
является выбор числа испытуемых элементов
N и длительности эксперимента
ТЭ
или числа r. При субъективном
выборе учитывают стоимость элемента,
наличие специализированных лабораторных
стендов, стоимость испытания одного
элемента, предварительные знания вида
распределения Р(t), величин
![]() и т.п.
и т.п.
Одним из
распространенных планов испытаний
является план NVN,
когда выбирается относительно большое
(для ТСА) число однотипных элементов N,
N>80-100, отказавшие в
моменты tj элементы
не восстанавливают, сам эксперимент
длится до отказа всех N
элементов, т.е.
![]() .
Проведение опытов и обработка данных
tj, j=1,2,…,
N при этом упрощаются, но
длительность ТЭ
может оказаться большой, что удорожает
испытания (подобный план "опасен"
при испытаниях элементов с нормально
распределенными наработками).
.
Проведение опытов и обработка данных
tj, j=1,2,…,
N при этом упрощаются, но
длительность ТЭ
может оказаться большой, что удорожает
испытания (подобный план "опасен"
при испытаниях элементов с нормально
распределенными наработками).
Обработка
данных tj, j=1,2,…,
N направлена на получение
статистических распределений надежности
![]() и оценок параметров надежности
и оценок параметров надежности
![]() .
Для этого отрезок [0, ТЭ]
разбивается на q
эквидистантных интервалов с примерной
длиной
.
Для этого отрезок [0, ТЭ]
разбивается на q
эквидистантных интервалов с примерной
длиной
tТЭ/(1+3,3 lg N)
с центрами ti, i=1,2,…, q (рис. 2.36 а). Подсчитывается число отказов Ni, приходящихся на каждый i-й интервал длины t (рис. 2.36 б).

Рис. 2.36 – К обработке результатов испытаний элементов на надежность
На рис. 2.36-а крестиками хх отмечены моменты отказа испытуемых элементов и соответствующие значения наработок до отказа tj, j=1,2,…, N. На рис. 2.36-б показаны интервалы t с центрами ti, i=1,2,…, q и соответствующие численности Ni.
При выборе числа q надо учитывать, что q<<N, примерно q0,1N, кроме того Ni 2 для всех i=1,2,…, q. Если некоторые Ni малы или равны нулю, то допустимо объединять два соседних интервала в один и перенумеровать ti, Ni, ti и изменить число q.
Далее определяются несмещенные состоятельные оценки параметров распределений:
![]()
![]()
(оценки
![]() можно найти и по другим формулам
можно найти и по другим формулам
![]()
![]()
но при малом
q величины
![]() могут отличаться от
).
могут отличаться от
).
Вычисляются ординаты статистических распределений:
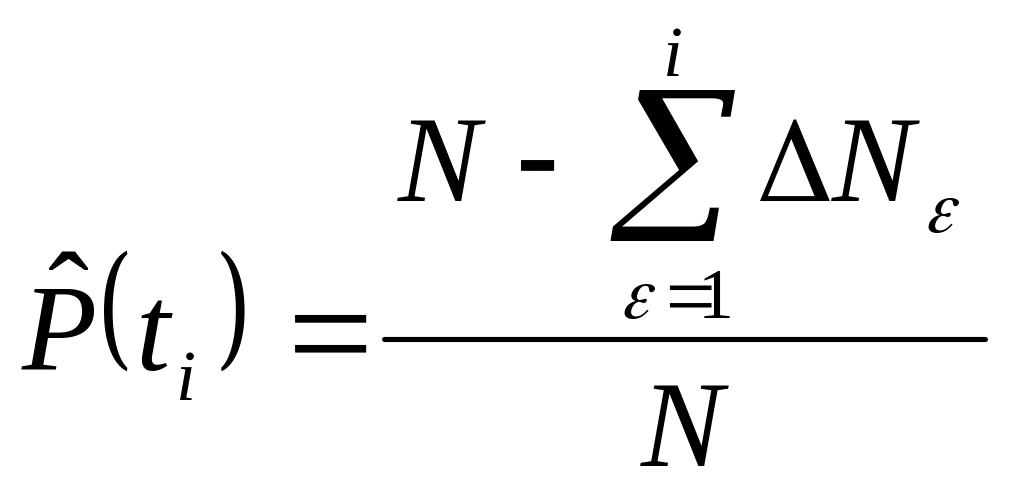 ,
i=1,2,…,q
,
i=1,2,…,q
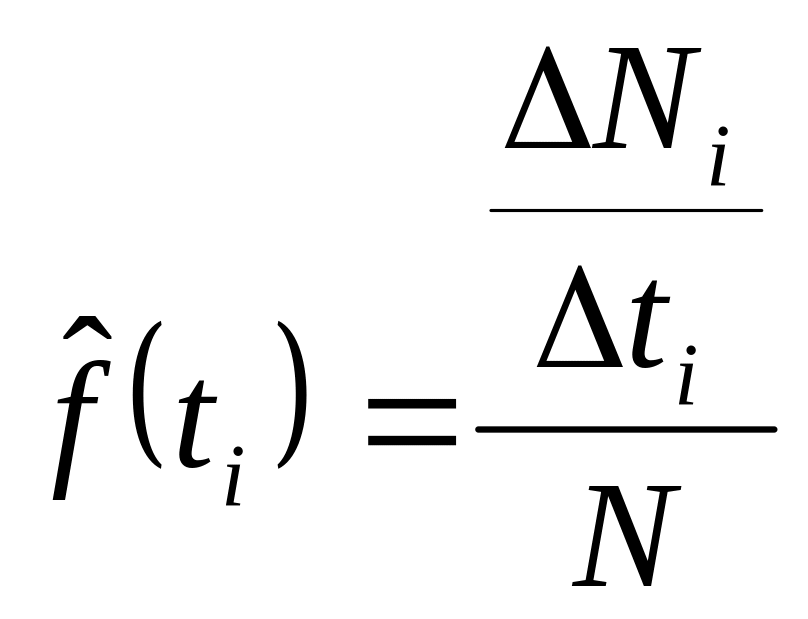 ,
i=1,2,…,q
,
i=1,2,…,q
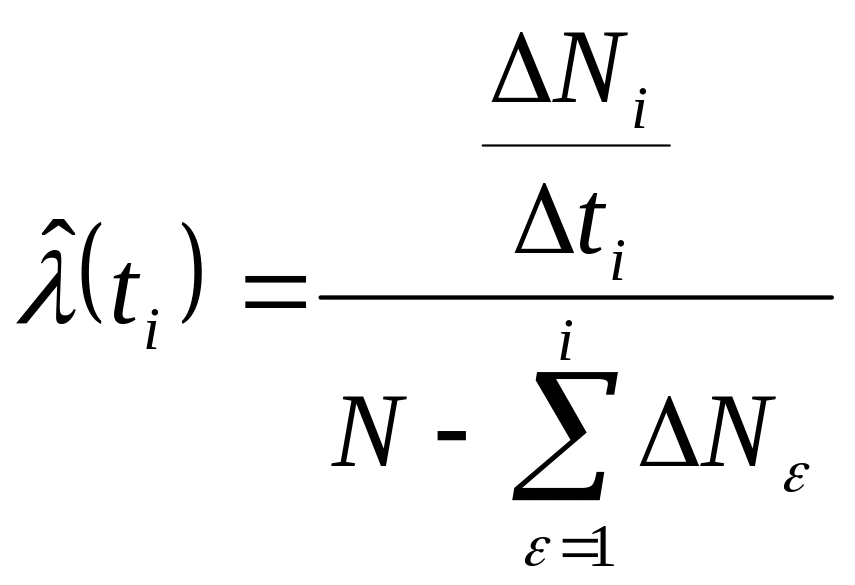 ,
i=1,2,…,q-1
,
i=1,2,…,q-1
где ti - длина неэквидистантного интервала.
Строятся
графики статистических распределений
оценок
![]() ,
,
![]() и
и
![]() (рис. 2.36-в)
(рис. 2.36-в)
Эти графики используются для выдвижения гипотезы о виде теоретического закона распределения вероятностей наработок. Напомним ряд характерных особенностей наиболее распространенных теоретических законов распределения:
-нормальное
распределение
![]() характеризуется симметричностью и
совпадением моды и медианы с оценкой
характеризуется симметричностью и
совпадением моды и медианы с оценкой
![]() (которая наряду с
(которая наряду с
![]() уже известна); для нормального распределения
приблизительно выполняются правила
"двух- и трех сигм":
уже известна); для нормального распределения
приблизительно выполняются правила
"двух- и трех сигм":
0,95 N
точек tj (![]() -2
-2
![]() ,
+2
)
,
+2
)
0,997 N точек tj ( -3 , +3 )
наконец, для нормального распределения можно назвать большое число (более 6-8) равновероятных причин отказов элементов;
-экспоненциальное
распределение характеризуется примерным
постоянством
![]()
и выполнением равенств
![]() ;
;
![]() ;
;
Указанные
особенности распределений, визуальный
анализ графиков и учет возможных
физических моделей отказов элементов
позволяют выдвинуть так называемую
нулевую гипотезу Н0
о согласии статистического распределения
тому или иному теоретическому закону
распределения вероятностей с эмпирическими
параметрами
или, для однопараметровых законов,
только
![]() .
.
Для проверки гипотезы применяют известные критерии согласия Пирсона (называемый иногда "хи-квадрат") и, реже, Колмогорова.
При
определении оценок параметров кроме
их точечных значений часто требуются
их интервальные оценки, характеризующие
точность найденных величин
и/или
![]() .
Эти так называемые доверительные
интервалы 1,
2
для tН
определяют из равенства
.
Эти так называемые доверительные
интервалы 1,
2
для tН
определяют из равенства
Вер{![]() - 1<tH<
+ 2}=Рдов,
- 1<tH<
+ 2}=Рдов,
где Рдов, - доверительная вероятность, задаваемая при расчете обычно из диапазона (0,80; 0,99). Кроме того, при решении задачи выбирают закон распределения случайной величины (обычно - нормальный) и затем по таблицам интеграла Лапласа находят 1=2=. Таким образом, истинное значение параметра tН определено с погрешностью и найдены "пессимистическая" - и "оптимистическая" + граничные значения средней наработки до отказа.
Величина 1=2= зависит от числа N используемых наработок на отказ tj. Естественно при росте N погрешность убывает. Этот факт иногда используется для определения такого числа необходимых испытуемых элементов N в плане [NVN], которое бы обеспечивало заданную погрешность определения оценок параметров или .
Определяемое таким путем число элементов обычно завышено по сравнению с числом N, подбираемым на основе эмпирических знаний.
