Функциональные показатели ремонтопригодности

Вероятность своевременного восстановления работоспособного состояния элемента за время t^в задана так:

Q(t^в)=Вер{того, что Т^В<t^в}= Вер{Т^В<t^в}

Эта функция равна нулю при t^в=0 (ремонт нельзя закончить раньше его начала) и равна 1 при t^в= (рано или поздно, но ремонт должен завершиться). Неубывающая функция своевременного завершения ремонта показана на рис. 2.34

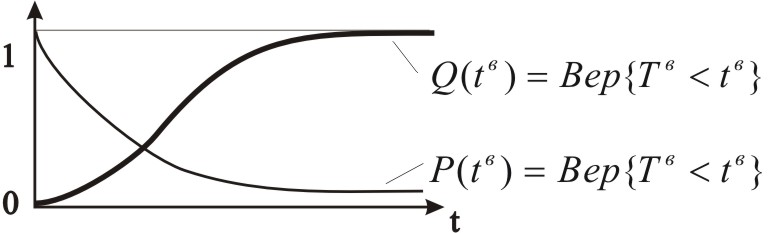
Рис. 2.34 – Графики показателей восстановления элемента

Можно ввести и другую, "негативную" вероятность незавершенности ремонта элемента к заданному моменту времени t^в (т.е. несвоевременное завершение ремонта).

P(t^в)=Вер{того, что Т^В>t^в}= Вер{Т^В>t^в}

Ремонт элемента никогда не завершится до момента t=0, поэтому Р(0)=1, а при t^в= он (ремонт) будет наверное закончен и случайное событие Т^В невероятно, следовательно Р()=0.

Невозрастающая функция "незавершенки" Р(t^в) также показана на рис. 2.34.

События Т^В>t^в или Т^В<t^в образуют полную группу независимых несовместимых случайных событий, поэтому

Q(t^в)+P(t^в)=1

Дифференциальный закон распределения вероятностей своевременного завершения ремонта

или функция плотности вероятности восстановления отказавшего элемента.

Интенсивность завершения ремонта характеризуется условной вероятностью своевременного восстановления элемента при условии. что элемент еще не восстановлен к этому моменту времени t:

Статистические распределения восстановления определяются по экспериментальным данным, полученным при исследовании ремонтов однородных элементов. Обозначим:  - число восстановленных элементов на малом интервале времени t^в, N(t^в) – общее число восстановленных элементов до момента времени t^в, N-N(t^в) - число еще не отремонтированных к моменту t^в элементов.

Статистические распределения завершенности и незавершенности ремонтов имеют вид

, 0 t^в<

, 0 t^в<

Статистические функции плотности и интенсивности таковы

,

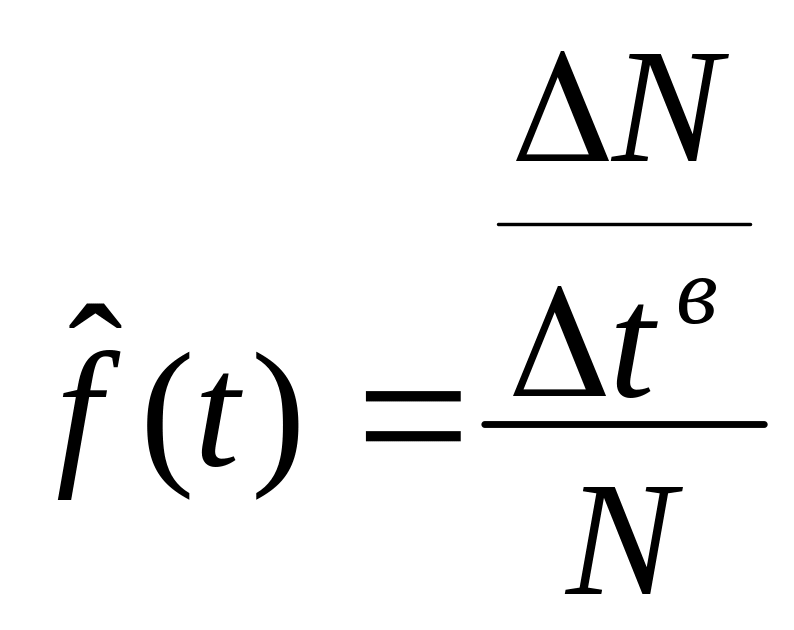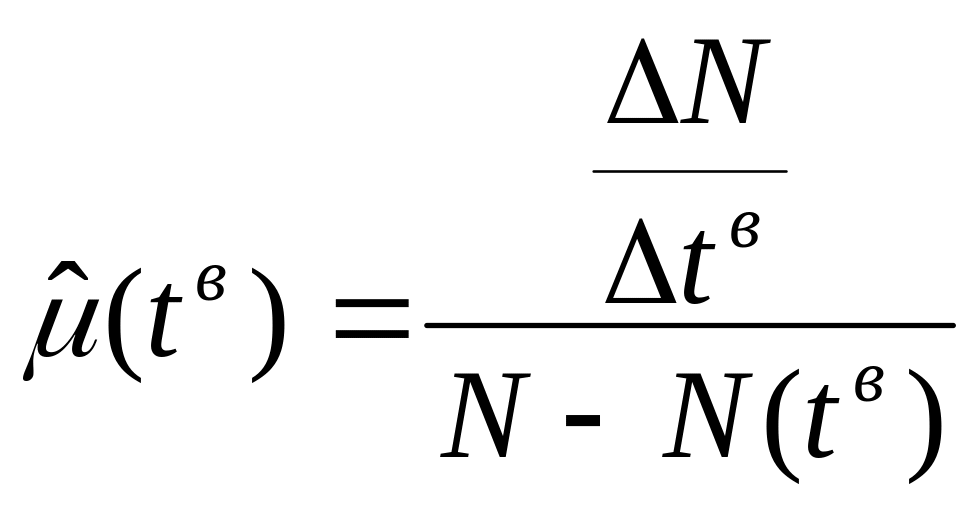
При все эти статистические функции сходятся по вероятности к соответствующим законам распределения.

Числовые показатели ремонтопригодности

К числовым показателям относятся среднее время восстановления

и, реже, дисперсия времени восстановления

Несмещенные и состоятельные оценки и определяются по экспериментальным длительностям ремонта N однородных элементов t_j^в, j=1,2,…, N:

,

Экспоненциальное распределение вероятности восстановления

Для описания поведения случайной величины Т^В чаще всего используют экспоненциальное (показательное) распределение

,

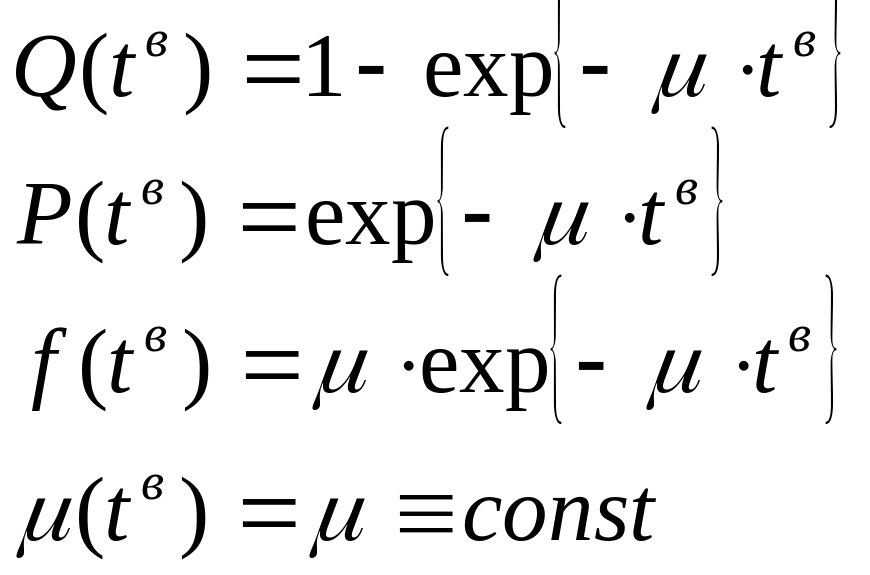
Графики функциональных показателей приведены на рис. 2.35.

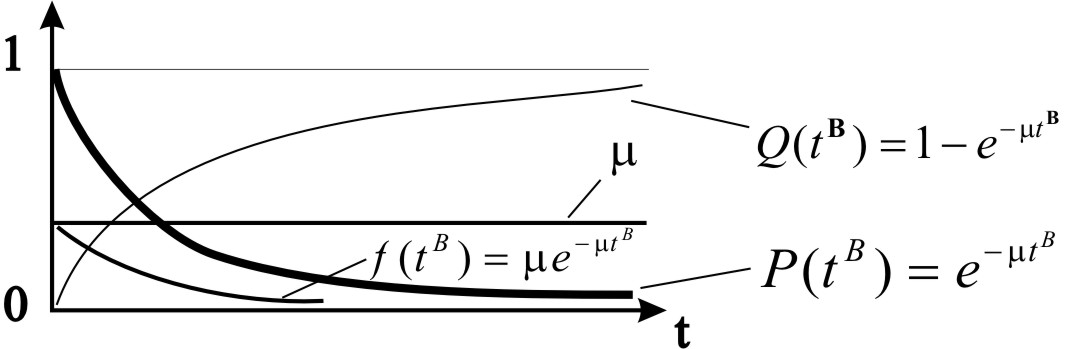
Рис. 2.35 – Графики изменения показателей восстановления элемента для экспоненциального распределения

Экспоненциальное распределение получило широкое применение при исследовании ремонтопригодности элемента.

Комплексные показатели ремонтопригодности

Самовосстанавливающаяся система "элемент – обслуживающий персонал" часть времени находится в работоспособном состоянии, а часть (иногда значительную) – в состоянии восстановления. Система считается тем лучше, чем больше доля времени, когда она работоспособна или готова к выполнению своих функций. Степень работоспособности системы "элемент – обслуживающий персонал" характеризуется рядом так называемых коэффициентов готовности, косвенно учитывающих безотказность и ремонтопригодность элемента и обслуживающего персонала.

Функция готовности К_Г(t) есть вероятность того, что система будет работоспособной в произвольный момент времени t₀. Если этот момент времени t₀ достаточно удален от нуля и в системе имеет место установившийся или стационарный режим функционирования, то функция готовности К_Г(t) превращается в коэффициент готовности К_Г, численно равный средней доле времени, когда система работоспособна, от общего времени ее эксплуатации

Для экспоненциальных распределений случайных величин Т и Т^В коэффициент готовности К_Г находится по формуле

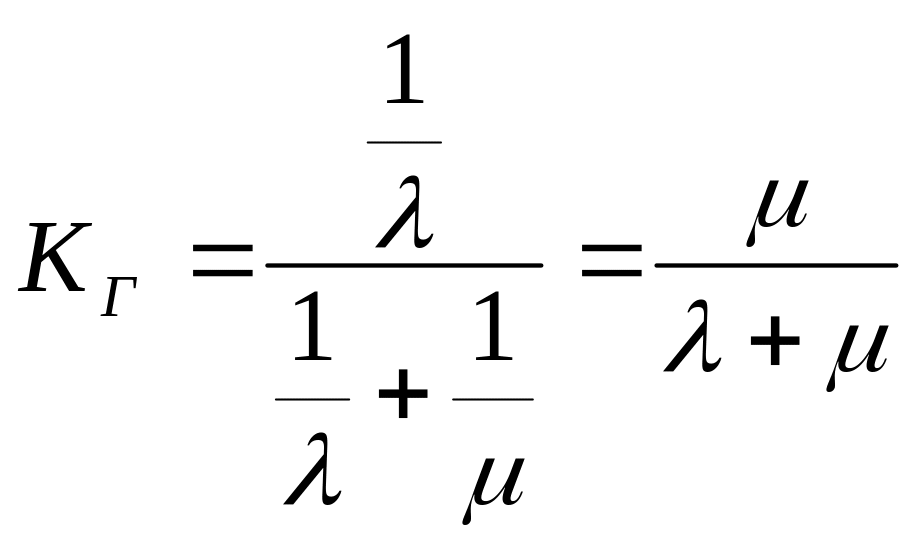
Отметим что стационарный коэффициент готовности К_Г не зависит от вида распределений (хотя К_Г(t) зависит от распределений Q(t) и Q(t^в)) случайных величин Т и Т^В.

Статистическая оценка определяется по результатам надежностных испытаний N систем "элемент – обслуживающий персонал":

где N(t₀) – число работоспособных систем в "удаленный" момент времени t₀. Оценку можно найти и по известным величинам ,

Коэффициент готовности К_Г изменяется от 0 до 1. Если восстановление проводится быстро и t_Н^в малό относительно t_Н, то К_Г1. Иначе, при длительных ремонтах и низкой безотказности, когда t_Н^в великό, а t_Н – малό, коэффициент готовности К_Г0. Серийные технические средства автоматизации имеют К_Г0,7-0,9.

В некоторых (немногочисленных) случаях ремонтопригодность и безотказность элемента характеризуют коэффициентом простоя К_П:

К_П=Вер{того, что элемент находится в ремонте в удаленный момент времени t₀}.

Этот стационарный коэффициент простоя определяется через известные t_Н^в и t_Н

или через К_Г

К_П=1- К_Г

(ибо система "элемент – обслуживающий персонал" находится либо в работоспособном состоянии, либо в ремонте).

Коэффициент оперативной готовности К_ОГ() равен вероятности того, что элемент работоспособен в удаленный момент времени t₀ и будет исправным на отрезке времени [t₀, t₀+]. Коэффициент К_ОГ() можно выразить через К_Г и условную вероятность безотказной работы элемента Р(t₀, ) на интервале [t₀, t₀+] при условии его исправного состояния в момент t₀^.

Для экспоненциального закона вероятность Р(t₀, ) не зависит от расположения отрезка  на числовой оси времени, а зависит только от величины 

Р(t₀, )=Р()=е^-

Поэтому для экспоненциально распределенных Т и Т^В коэффициент оперативной готовности равен

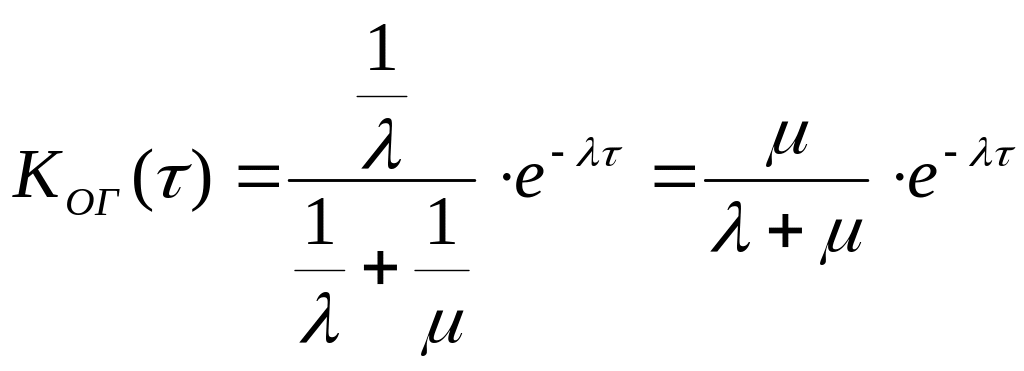
Коэффициент К_ОГ() убывает с ростом времени  и почти всегда меньше К_Г, только при =0 имеем К_ОГ(0)=К_Г.

Существует ряд ТСА, которые периодически выводятся на время t_ПР из эксплуатации, например, для тарировки, профилактики и др. Это время вынужденного "простоя" t_ПР элемента не связано непосредственно с его безотказностью и ремонтопригодностью и не учитывается при определении t_Н^в и t_Н, а следовательно, и К_Г и К_ОГ. Если t_ПР - случайная величина и ее среднее значение М{ t_ПР } соизмеримо с t_Н^в и t_Н, то безотказность и ремонтопригодность элемента с вынужденными простоями следует характеризовать коэффициентом технического использования

который всегда меньше К_Г.