Суперпозиции экспоненциальных распределений

Для приближения статистических распределений сложного вида известными ("хорошими") теоретическими распределениями применяют суперпозиции экспоненциальных законов

где: f₁(t)=₁exp-₁t, f₂(t)=₂exp-₂t, с₁,с₂ – весовые множители, с₁+c₂=1; величина с₁ подбирается наряду с интенсивностями ₁, ₂, из условия близости статистической плотности и нового закона f_c(t).

Для подобной суперпозиции имеем

P_с(t)=

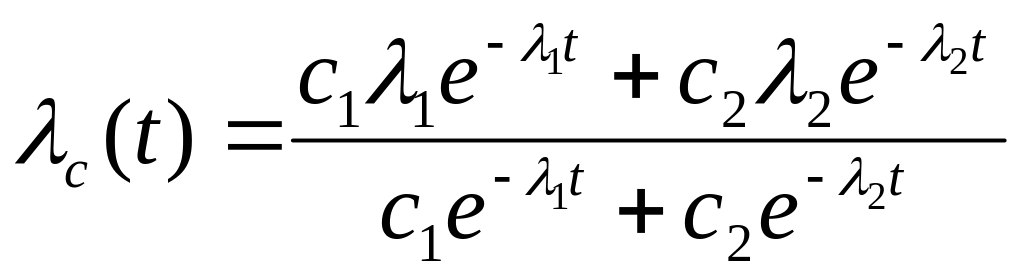
_c(0)= c₁₁+ c₂₂

Средняя наработка до отказа t_НС равна

Вариацией параметров ₁, ₂, c₁ можно добиться хорошей аппроксимации статистических интенсивностей на периодах приработки элемента. Если положить ₂>₁, то при малых t функция exp{-₂t} быстрее стремится к нулю, чем exp{-₁t}. Поэтому при больших t имеем _c(t)₁ (рис. 2.31).

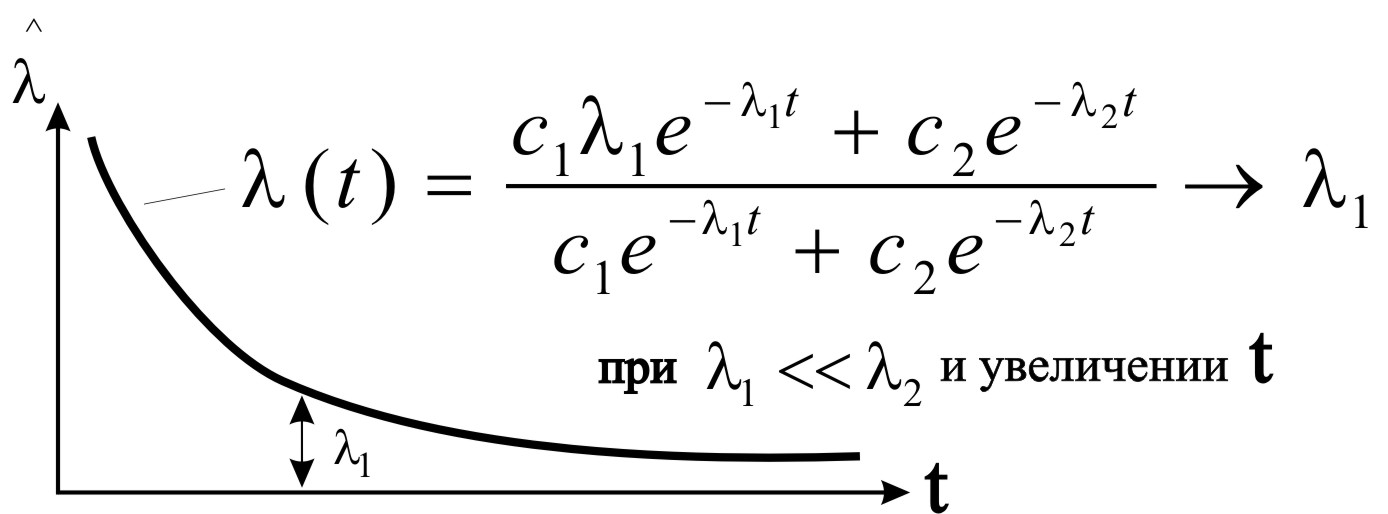
Рис. 2.31 – Суперпозиция двух экспоненциальных распределений

Для описания поведения элементов с внезапными и постепенными отказами применяют суперпозицию экспоненциального и усеченного нормального распределений

где с₁+с₂=1.

Весовые множители с₁, с₂ характеризуют частоты внезапных и постепенных отказов. При одинаковой частоте этих отказов с₁=с₂=0,5. Варьируя с₁ (или с₂) можно заметно влиять на форму интенсивности _c(t).

2.5. Ремонтопригодность технических элементов

Восстанавливаемый элемент после каждого j-го отказа ремонтируется обслуживающим персоналом и будучи полностью исправным снова включается в работу (рис. 2.32):

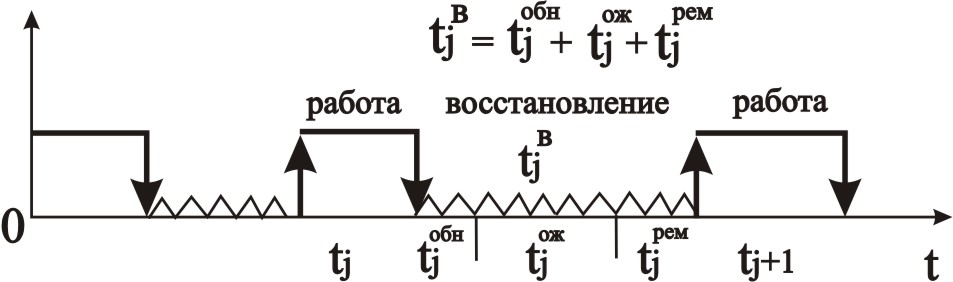
Рис. 2.32 – Схема режима восстановления элемента

Продолжительность такого ремонта t_j^в есть значение случайной величины Т^В - длительности восстановления.

В общем случае процесс восстановления элемента можно разделить на три последовательных операции:

- обнаружение (проявление) отказа; осуществляется чаще всего человеком – оператором за случайное время t^обн, реже – автоматическим устройством сигнализации;

- ожидание ремонтного персонала; характеризуется случайным временем ожидания t^ож;

- поиска ошибки или дефекта элемента, вызвавших его отказ, и собственно ремонта; выполняется ремонтным персоналом за случайное время t^рем.

Во всех трех операциях существенную роль играет человек – оператор и/или человек – ремонтник. Поэтому случайное время восстановления j-го отказа элемента

t_j^в = t_j^обн + t_j^ож + t_j^рем

фактически характеризует систему "элемент – обслуживающий персонал", где под обслуживающим персоналом понимается человек – оператор и человек – ремонтник.

В некоторых системах "элемент – обслуживающий персонал" математическое ожидание времени восстановления М{t^в} может быть пренебрежимо мало (относительно, например, t_Н элемента). Это имеет место при автоматическом обнаружении отказов, когда М{t^обн}0, при хорошем функционировании ремонтной службы (М{t^ож}0) и, самое главное, при замене отказавших элементов на аналогичные исправные устройства.

Режим функционирования такой системы характеризуется мгновенным восстановлением элементов в случайные моменты времени t_j, j=1,2,3,… с пренебрежимо малыми продолжительностями восстановления (рис. 2.33).

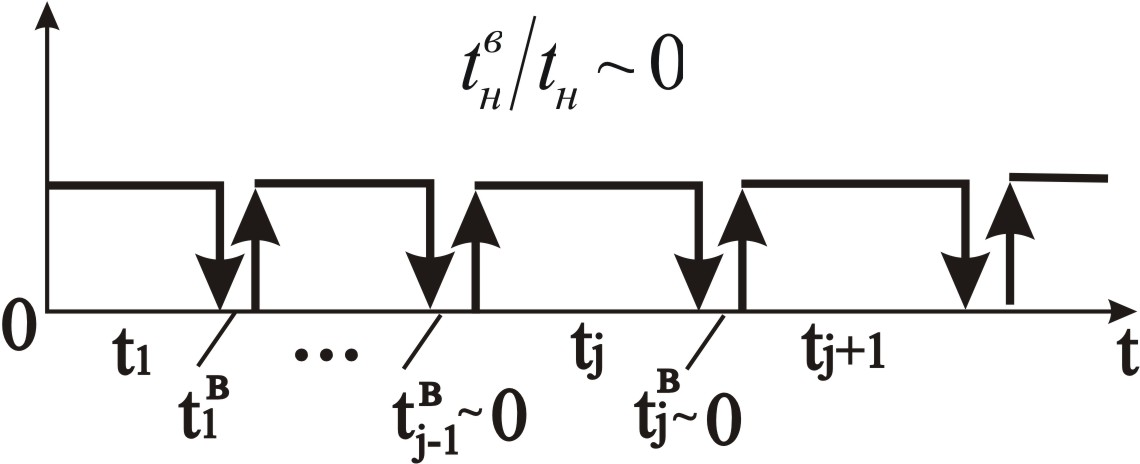
Рис. 2.33 – К понятию режима мгновенного восстановления

Поток отказов {t_j, j=1,2,3,…} элемента с мгновенным восстановлением описывается уже известными функциональными и числовыми показателями

Q(t), P(t), f(t), (t), t_Н, t_j, ², P(t_h)

и не нуждается в каких – либо дополнительных характеристиках.

Режим функционирования с мгновенным восстановлением связан с значительным удорожанием системы "элемент – обслуживающий персонал",

так как предполагает автоматизацию обнаружения отказов, повышения качества работы ремонтного персонала и создания парка резервных элементов. Поэтому подобные режимы функционирования экономически оправданы при эксплуатации ответственных элементов, отказы которых ведут к возникновению аварийных ситуаций или значительному экономическому ущербу.

Для большинства надежностных задач не удается обосновать допущение о мгновенности восстановления элементов и поэтому необходимо учитывать продолжительность восстановления Т^В и вводить функциональные и числовые показатели ремонтопригодности.