Распределение Релея

Это однопараметровое распределение является частным случаем распределения Вейбулла при m=2 и к=1/2², где ² – дисперсия наработки на отказ (параметр распределения Релея).

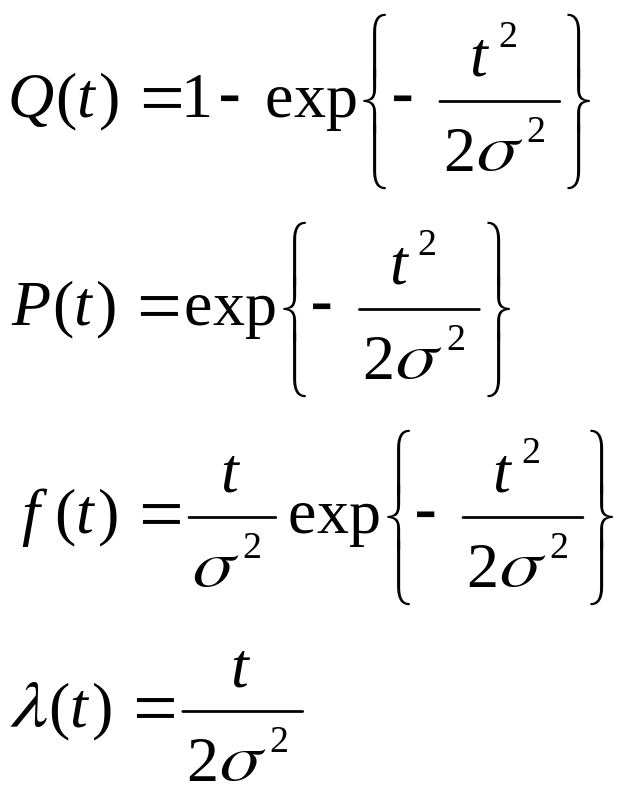
Графики распределений показаны на рис. 2.28

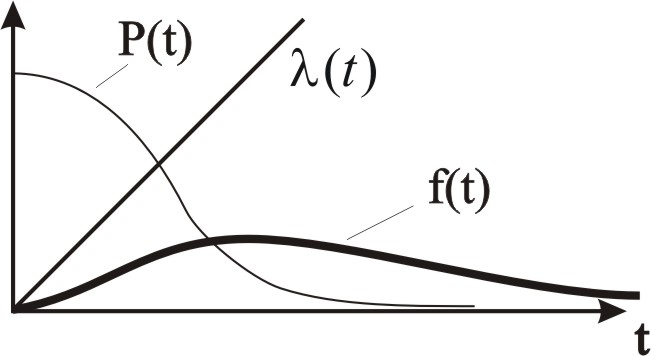
Рис. 2.28 – Графики показателей надежности для распределения Релея

Построение графиков Q(t), P(t) и (t) не вызывает затруднений. Построение кривой требует пояснений. При t=0 получаем f(0)=0, при t имеем неопределенность . Однако, после применения правила Лопиталя, убеждаемся, что быстрее стремится

к нулю при t, чем функция t/² стремится к  при t, т.е. f()=0. При t(0,) функция f(t) положительна и имеет единственную стационарную точку, являющейся точкой максимума.

Распределение Релея имеет ограниченное применение для описания наработок на отказ радиоэлектронных устройств.

Нормальное распределение

Нормальный закон распределения вероятностей описывает поведение случайных величин в диапазоне [-,+] и обладает функциональными характеристиками

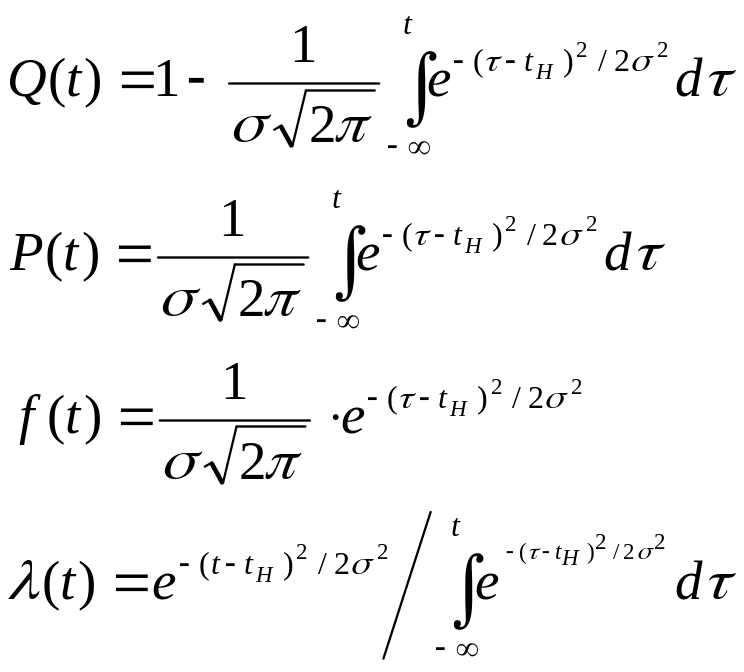
Эти зависимости зависят от двух параметров – средней наработки до отказа t_Н и дисперсии ². Характерной особенностью нормальной плотности вероятности является ее симметричность относительно точки t=t_Н, а также совпадение моды и медианы с t_Н (рис. 2.29).

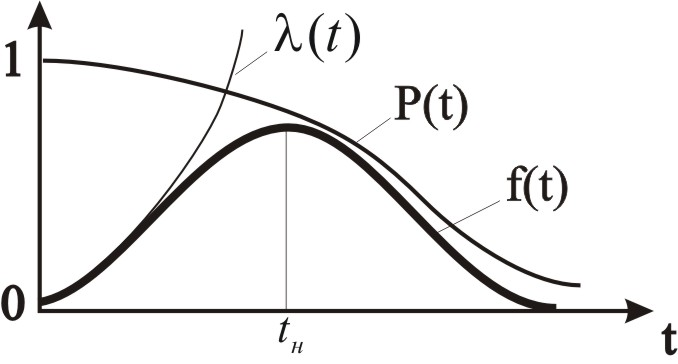
Рис. 2.29 - Графики показателей надежности для нормального закона

Нормальное распределение можно применять для описания положительных наработок на отказ t_Н только в том случае, если t_Н существенно отличается от нуля, например, при t_Н(2-3). В этих случаях допустимо "пренебрегать" значениями характеристик при "отрицательном" времени t.

В частности, при t_Н=3 отбрасываемая доля плотности f(t), относящаяся к отрицательным t, составляет 0,15%; при t_Н=2 доля не учитываемой плотности f(t) (показана штриховкой на рис. 2.30) не превышает 2,5%. Такие погрешности при аппроксимации экспериментальных наработок на отказ вполне допустимы и не препятствуют использованию обычного нормального распределения.

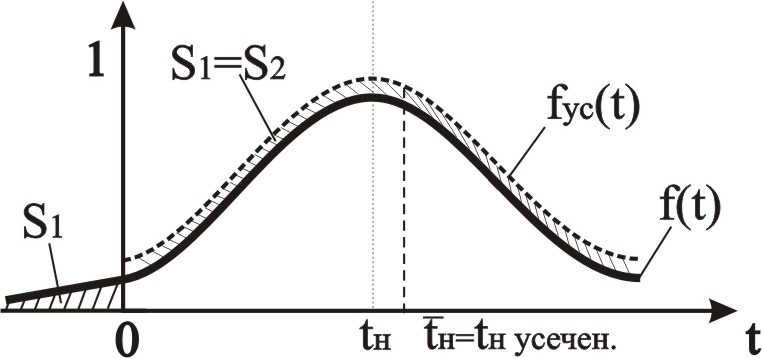
Рис. 2.30 – К получению усеченного нормального распределения

Отметим, что нормальное распределение целесообразно применять для описания постепенных отказов, возникающих по ряду (не менее 6-8) причин. Кроме того, нормальное распределение целесообразно использовать для описания отказов на периоде физического износа элементов.

Усеченное нормальное распределение

Усеченное нормальное распределение получают из обычного нормального закона в тех случаях, когда средняя наработка до отказа t_Н мала относительно среднего квадратического отклонения : t_Н<2. В этом случае "неучет" плотности вероятности f(t), при "отрицательном" времени дает значительную погрешность и поэтому вводится новая – усеченная – функция плотности (рис. 2.30)

f(t)=cf(t), t[0,]

f(t)0, t(-,0)

Поправочный множитель c определяют из условия нормировки усеченной плотности

или, если определена на отрезке (0, t₀), t₀>0,

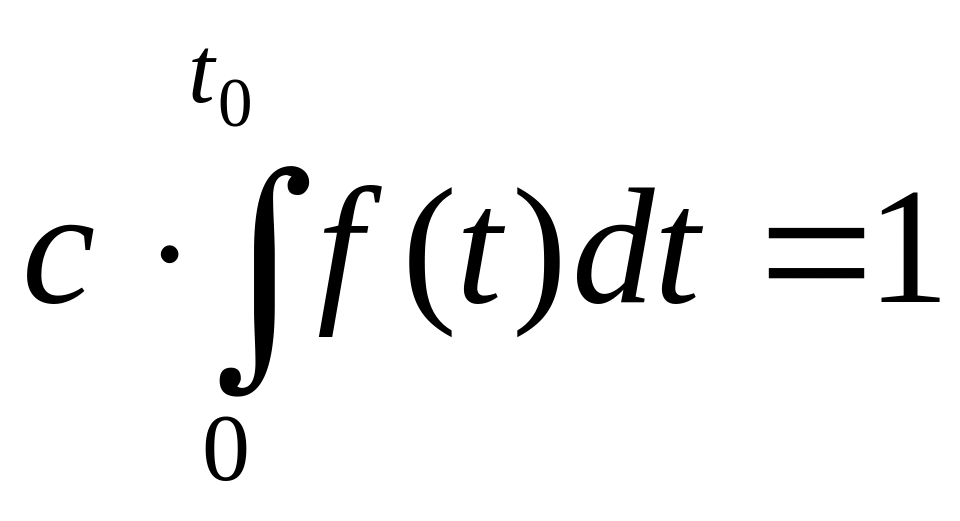
Функциональные характеристики усеченного нормального распределения имеют вид

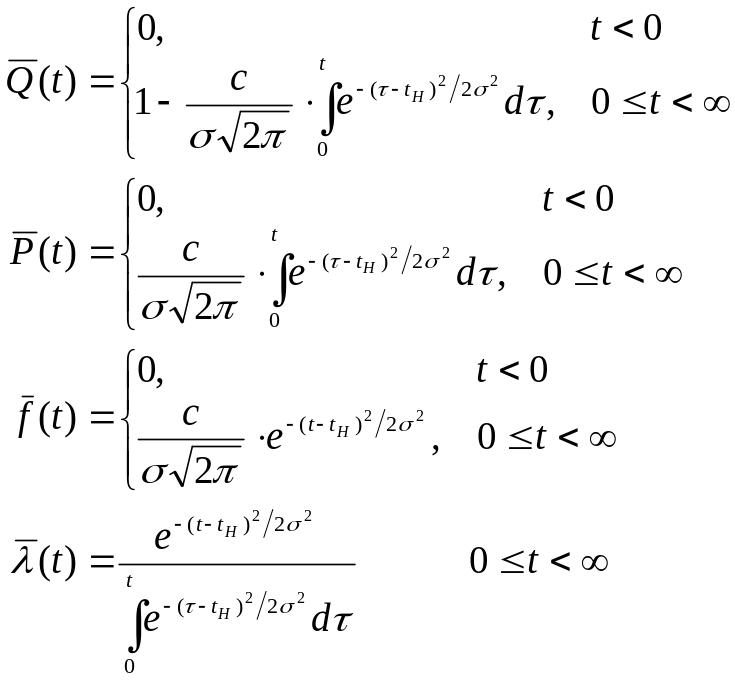
Числовые показателиt_Н и ² усеченного распределения можно найти через известные t_Н и ² и параметр c:

t_Н=t_Н+с₁,

²= ²(1-с₁²-с₁t_Н1/)

где с₁= (cexp{- /2² }/ .

Для описания надежности серийных ТСА усеченное нормальное распределение применяется редко, ибо для технических средств автоматизации характерно большое отношение t_Н к : t_Н/ > 2-3