2.4. Основные законы распределения наработки до отказа

Поведение случайной величины – наработки до отказа Т – может быть описано тем или иным теоретическим законом распределения вероятностей Q(t) или, чаще P(t). Опытным путем установлено, что поведение наработки до отказа Т технических средств автоматизации удовлетворительно описываются небольшим числом (не более 4-5) законов распределения: Вейбулла, экспоненциальным, нормальным, усеченным нормальным и суперпозицией указанных законов.

Распределение Вейбулла

Функциональные показатели надежности случайной величины Т подчиняются двухпараметровому распределению Вейбулла вида

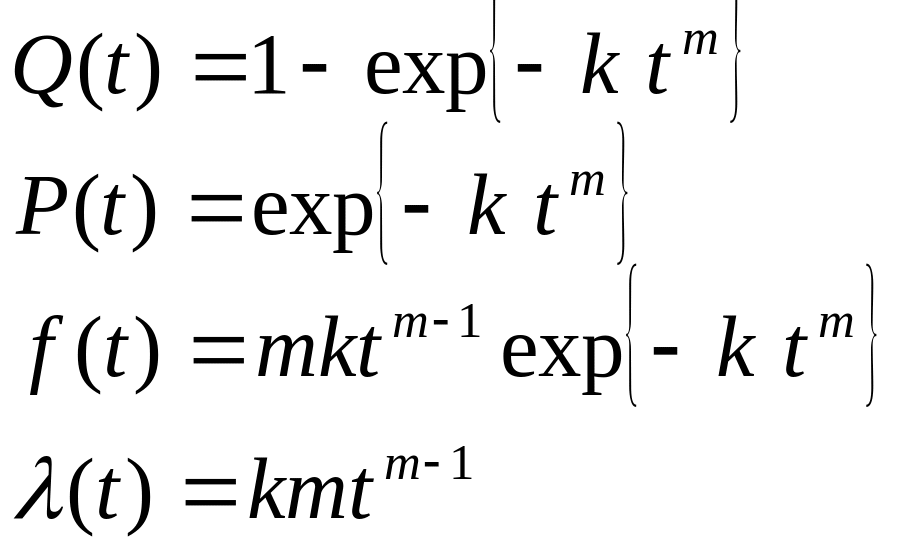
где k и m – числовые параметры, определяемые по результатам испытаний элементов на надежность t_j, j= . Параметр k определяет масштаб распределения, при вариациях k кривая распределения "сжимается" или "растягивается".

Параметр m характеризует вид распределения, при m=1 получаем экспоненциальное (показательное) распределение, при m=2 – распределение Релея (см. ниже). Чаще всего m выбирают из интервала (0,5; 2,5).

Графики распределения Вейбулла для трех характерных значений параметра m= 1;2;0,5 приведены на рис. 2.24

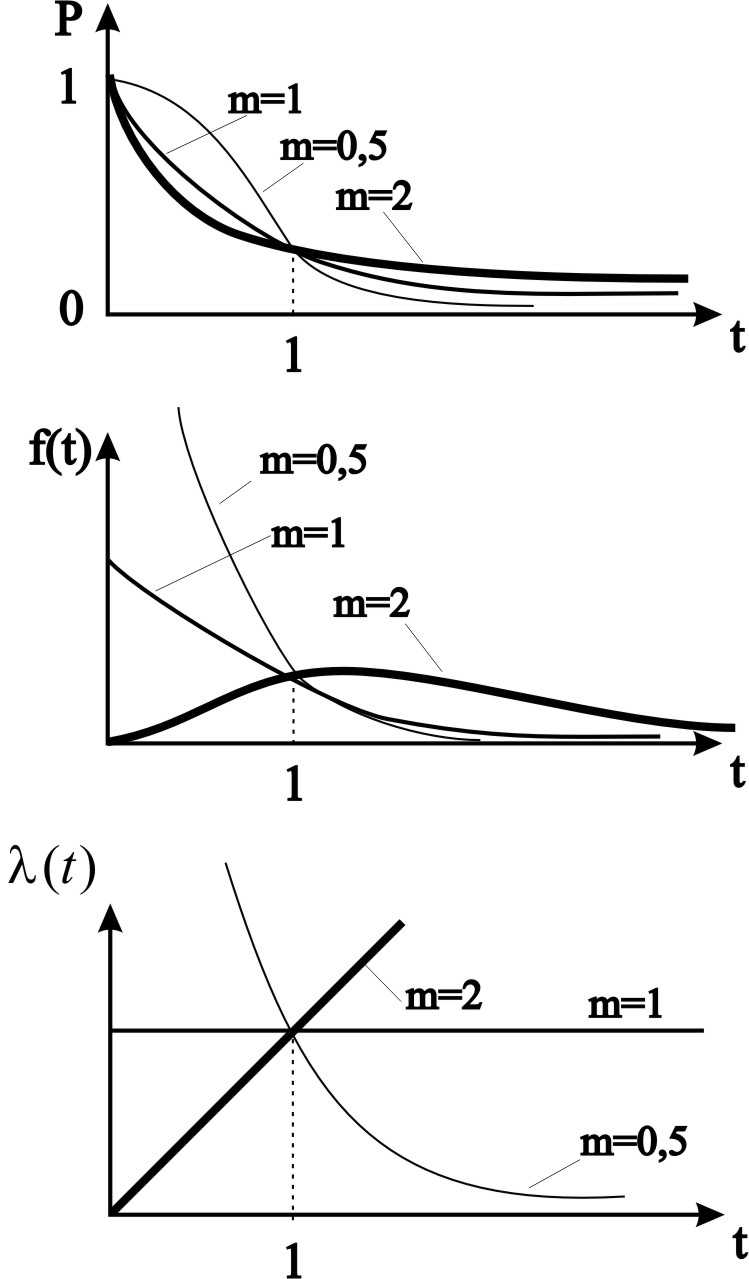
Рис. 2.24 – Показатели надежности для распределения Вейбулла

Для распределения Вейбулла средняя наработка до отказа определяется достаточно сложно:

где Г() – гамма-функция

Удобнее находить значения Г() по таблицам гамма-функций, имеющимся в большинстве математических справочников.

Распределение Вейбулла с параметром m(0,5…2,5) находит широкое применение для описания наработки до отказа многих сложных радиоэлектронных устройств, статистические интенсивности отказов которых являются монотонно возрастающими или убывающими функциями времени.

Экспоненциальное распределение

Экспоненциальное (показательное) распределение является частным случаем распределения Вейбулла при m=1, поэтому оно относится к однопараметровым законам распределения вероятностей. Этим параметром служит постоянная во времени интенсивность отказов . Обозначая параметр k через , получаем из распределения Вейбулла функциональные показатели экспоненциально распределенной наработки до отказа Т:

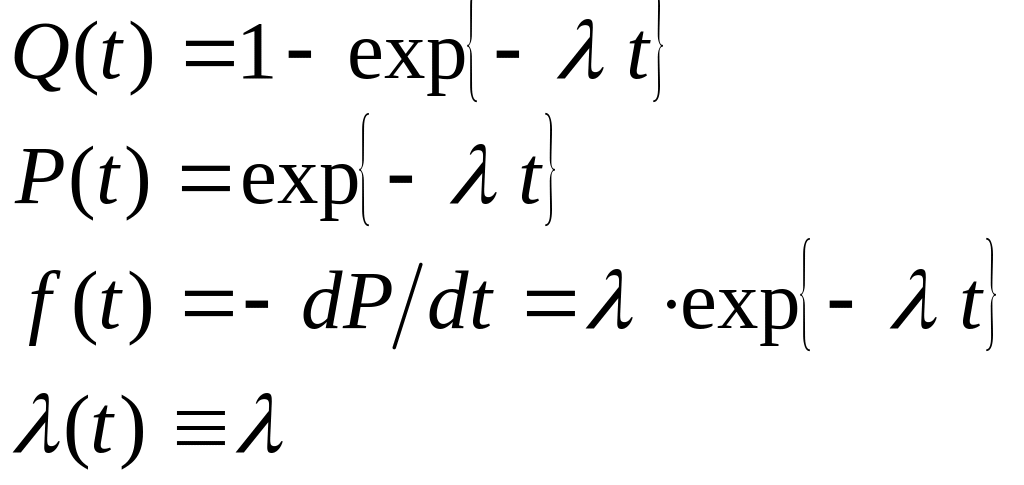
Графики этих зависимостей приведены на рис. 2.25

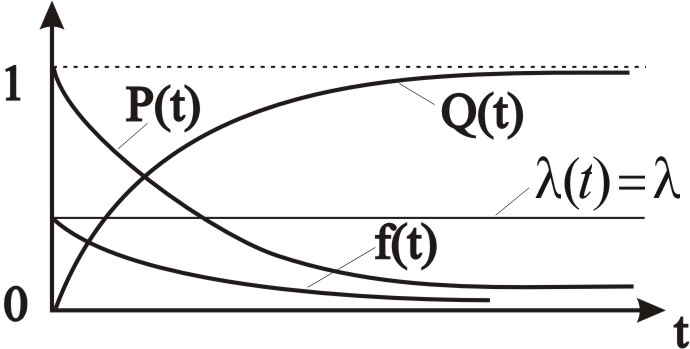
Рис. 2.25 – Графики показателей надежности для экспоненциального распределения

Средняя наработка до отказа t_Н равна

или более просто

Хотя дисперсия ² случайной величины Т не входит в зависимости Q(t), P(t), но во многих задачах полезно знание ²:

(для вычисления дисперсии требуется двукратное интегрирование по частям выражения (t-t_Н)²e^-).

Экспоненциальный закон распределения позволяет достаточно просто получать грубые оценки надежности элементов. Для этого следует разложить Q(t), P(t) в ряд Тейлора по степеням t в малой окрестности точки t=0 и удержать два первых члена ряда:

P(t)1-t, Q(t) t

Эти зависимости применимы при t<<1 или при t<<t_Н , т.е. их можно использовать для оценки надежности элемента на начальном периоде его работы, например, при t<(0,1-0,01)t_Н.

Если измерять время t в долях средней наработки до отказа t_Н, то можно вычислить приближенные значения вероятности безотказной работы P(t_h) в моменты времени t_h (табл. 2)

Таблица 2

Значения вероятности в моменты времени

	~0,37	~0,9	~0,99	~0,999	~0,9999

Из анализа табл. 2 следует, что из 1000 одинаковых элементов к моменту времени t_Н работоспособными будет ~370 элементов (а 630 элементов откажет); к моменту t_Н =0,1t_Н исправными останутся 900 элементов, а 100 элементов откажут и т.д..

Если P(t_h) рассматривать как гарантийный (желаемый) уровень надежности, то легко определить соответствующие гамма-ресурсы, равные t_h. Например, при =0,99 получаем t_0,01t_Н; при =0,9 имеем t_0,1t_Н и, наконец, при =0,37 получаем "большой" гамма-ресурс t_=t_Н (отметим, что подобным ресурсом t_Н будет обладать примерно каждый третий элемент, а остальные каждые два элемента откажут ранее момента t_h).

Применительно к типовым ТСА желаемый уровень надежности составляет 0,9-0,95, следовательно, гарантированный ресурс элементов достигает (0,1-0,01)t_Н (напомним, что все приведенные количественные соотношения справедливы для экспоненциально распределенной наработки до отказа Т).

При оценке условной вероятности работоспособности элементов на некотором интервале времени t требуется знание "расположения" t на числовой оси t, т.е. время работы элемента до начала интервала t. Не приводя доказательств, укажем, что для экспоненциального закона условная вероятность безотказной работы элемента P(t₁,t₂) на отрезке t = t₂-t₁ при условии его работоспособности до t₁, зависит только от длины этого отрезка и не зависит от его расположения на оси времени t (рис. 2.26).

Рис. 2.26 – К определению условной вероятности работоспособности элемента на отрезке [t₁, t₂] для экспоненциального распределения

где P(t₁,t₂) – вероятность безотказной работы на t = t₂-t₁; e ^-t₁, e ^-t₂ - вероятности исправной работы в моменты t₂ и t₁.

Экспоненциальный закон распределения хорошо описывает наработки до внезапного отказа сложных элементов, которые состоят из большого числа М разнородных деталей (частей) с интенсивностями _(t), =1,2,…,M, имеющими экстремумы в разные моменты времени t_, =1,2,…,M (рис. 2.27)

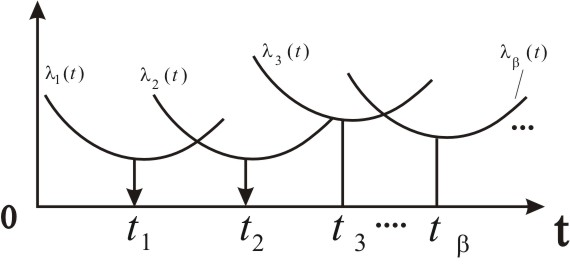
Рис. 2.27 – К возможности описания отказов элемента экспоненциальным распределением

Примерами таких элементов могут служить электронные устройства, средства вычислительной техники, пневмоавтоматики и другие ТСА.

Экспоненциальное распределение удовлетворительно описывает надежность ТСА, обладающих малым периодом приработки элементов и почти не достигающих периода старения (износа) из-за относительно быстрого морального износа и замены на более совершенные.

Экспоненциальное распределение широко применяется в практических надежностных расчетах, в частности при проектной оценке надежности элементов и систем. При расчетах надежности систем состоящих из большого числа элементов с неизвестными или "сомнительными" характеристиками надежности, всегда следует использовать экспоненциальное распределение, позволяющее наиболее просто получать расчетные показатели безотказности.