2.3. Числовые показатели надежности

Функциональные показатели надежности Q(t), P(t), f(t), (t) наиболее полно описывают поведение случайной величины Т – наработки до отказа элемента. Однако получение этих функциональных характеристик или хотя бы их статистических аналогов , , , вызывает значительные трудности, обусловленные длительными и дорогостоящими экспериментами с большим числом элементов, сложной математической обработкой экспериментальных данных и трудоемкой проверкой гипотез согласия. Поэтому при решении многих прикладных задач надежности широко используют числовые показатели надежности, оценки которых получают по экспериментальным данным более просто и более быстро, чем оценки функциональных показателей.

Средняя наработка до отказа

Этот показатель является математическим ожиданием времени безотказной работы элемента (наработки до отказа или наработки между отказами)

где t_Н – средняя наработка до отказа, М – символ операции математическое ожидание.

Более удобно вычислять t_Н по другой формуле:

А

При получении этой формулы интеграл А берется по частям, а выражение оказывается равным нулю, если неопределенность раскрыть с помощью правила Лопиталя. Среднюю наработку до отказа можно найти и по другим функциональным характеристикам Q(t) и (t):

, .

Оценка средней наработки до отказа определяется по известным из эксперимента значениям наработки до отказа или между отказами t_j, j= :

Оценка несмещенная и состоятельная, при N случайная величина . Оценка и сама имеет физическую размерность един. времени, значение часто указывается в техническом паспорте элемента и служит основной характеристикой его надежности.

Дисперсия наработки до отказа ²

Этот числовой показатель входит как параметр в так называемый нормальный закон распределения вероятностей (см. ниже), традиционно величина ² характеризует разброс значений наработок до отказа относительно средней наработки t_Н:

Оценка дисперсии определяется по экспериментальным наработкам до отказа (между отказами) t_j, j= :

,

где - среднее арифметическое потока отказов t_j. Эта оценка несмещенная и состоятельная, при N имеем .

При большом числе N, N>100 экспериментальных данных допустимо использовать и другую формулу

,

имеющую малую систематическую погрешность.

Гамма-процентный ресурс надежности

В ряде приложений принято измерять вероятность в процентах Р_пр(t), т.е. тогда 0Р_пр(t)100%. Зададим некоторый желаемый гарантийный уровень надежности %, например, 80% или 90%. Тогда гамма-процентный ресурс t_% - есть отрезок времени, на котором надежность элемента не ниже желаемой (или гарантийной) величины %: Р_пр(t) %.

Величина гамма-процентного ресурса t_% есть корень конечного уравнения Р_пр(t_%)= %, который легко определяется графически (рис. 2.22)

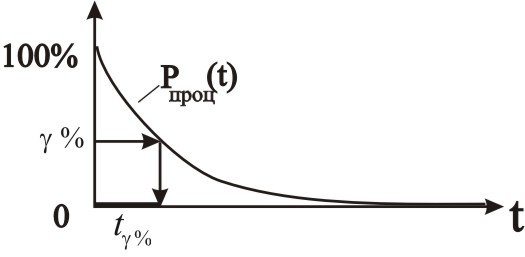
Рис. 2.22 – К определению гамма-процентного ресурса t_%

Удобнее, однако, использовать обычную вероятность P(t), изменяющуюся от 0 до 1, и задавать гарантийный (желаемый) уровень надежности , 01. Тогда гамма-ресурс t_ есть отрезок времени, на котором P(t) (рис. 2.22 а). Значение t_ есть корень уравнения Р(t_)= . Понятно, что t_= t_% (далее всюду будет применяться просто гамма-ресурс t_, имеющий физическую размерность времени).

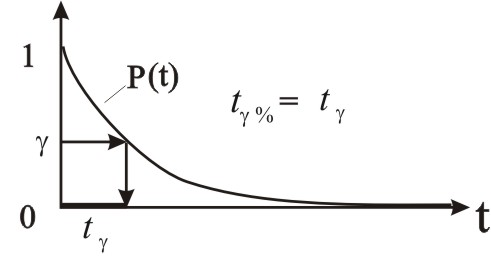
Рис. 2.22 а – К определению гамма-ресурса t_

Гамма-ресурс t_ зависит от двух факторов – надежности элемента, в частности функции P(t), и гарантийного уровня .

В этих условиях естественно стремление улучшить показатель надежности t_ простым уменьшением уровня , что, однако, приводит к уменьшению доли элементов, не отказавших до момента времени t_. Так,

например, при =0,9 получен гамма-ресурс t_=1000 часов. При этом из 1000 включенных элементов к моменту 1000 часов не откажет 900 элементов. Если понизить гарантийный уровень  до 0,3, то гамма-ресурс t_ возрастет до 4000 час., но при этом из 1000 элементов только 300 доработают до рубежа 4000 час. (т.е. статистическая достоверность показателя t_ =4000 будет очень низкой).

Так как часто приводится в технических паспортах элементов, то необходимо указание в них и гарантийного уровня . Для технических средств автоматизации, работающих в нормальных эксплуатационных условиях, считается приемлемым гарантийный уровень =0,9…0,95.

Вероятность безотказной работы в заданные моменты времени t_h

Для каждого типа элементов указываются характерные моменты времени t₁, t₂,…,t_h,…,t_K, для которых по экспериментальным данным определяются оценки , h=1,2,…,k. (рис. 2.23):

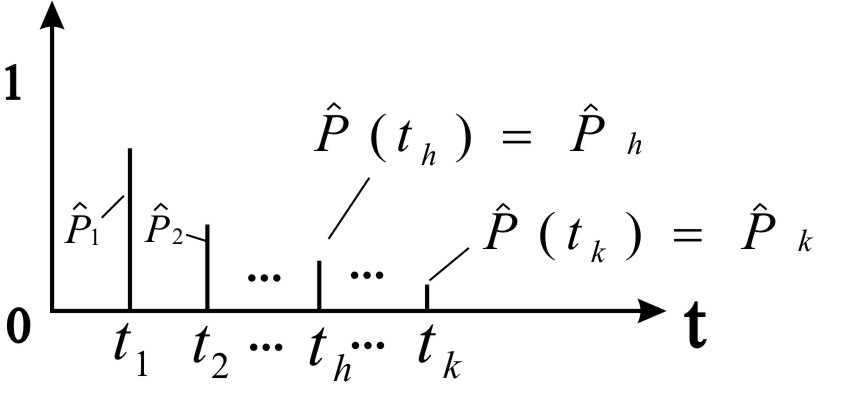
Рис. 2.23 – К определению оценки вероятности исправной работы элемента до заданного времени t_h

Значения , h=1,2,…,k часто приводятся в технических паспортах элементов. При этом для более надежных элементов используют бόльшие значения t_h, для менее надежных элементов – мéньшие t_h. Так, например, для средств пневмоавтоматики применяют ряд t_h=400, 1000, 2000, 4000, 8000 час., для средств вычислительной техники t_h=100, 200, 400, 1000, 2000 час.