3.3. Надежностный синтез технических систем

Под надежностным синтезом понимается конструирование простых технических систем с заданными (желаемыми) или экстремальными показателями надежности.

При таком синтезе обычно учитывают некоторые дополнительные ограничения на количество используемых элементов, их характеристики, стоимость создаваемой системы и т.п. В результате этого надежностный синтез сводится к задаче на условный экстремум выбранного нами показателя надежности, зависящего от дискретных, непрерывных и лингвистических переменных. Решение подобных задач в общей постановке вызывает серьезные затруднения, поэтому ниже рассматриваются некоторые частные задачи надежностного синтеза локальных систем и процедуры их приближенного решения.

Анализ задачи надежностного синтеза

В задачу оптимального синтеза входят:

• критерий оптимальности,

• независимые переменные,

• ограничения на переменные,

• связи между переменными.

Критерии оптимальности. В качестве критерия П в задачах надежностного синтеза обычно используют:

• среднюю наработку до отказа t_н^с,

• вероятность исправной работы системы P_c(t₀) в заданный момент

времени t₀, 0<t₀<.

Критерий П={t_н^с или Р_с(t₀)} в общем случае явно или опосредованно зависит от: структуры S системы; понятия отказа системы (ОС); вектора интенсивностей отказов  элементов, входящих в систему, т.е.

П=П(S, ОС, )

Структура S в данной задаче определяется только числом элементов, каждый из которых имеет два состояния: отказ или работоспособность. Тогда структура S₁ включает всего один элемент, структура S₂ – имеет 2 элемента, и т.д. Наконец, последняя структура S_n будет включать n элементов (число n определяется человеком-экспертом в зависимости от условий задачи).

Для произвольной структуры S_j , 1<j<n, возможны разные варианты соединения элементов, например, последовательное или параллельное включение. Будем обозначать каждый вариант структуры S_j верхним индексом h, h=1,2,3,…, d_j, т.е. получим запись S_j^h. Тогда для S₁ возможен только один вариант включения (рис. 3.49).

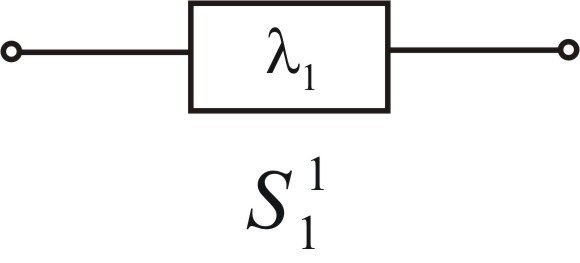
Рис. 3.49 – Пример структуры S₁

Для структуры S₂ возможны два варианта (рис. 3.50)

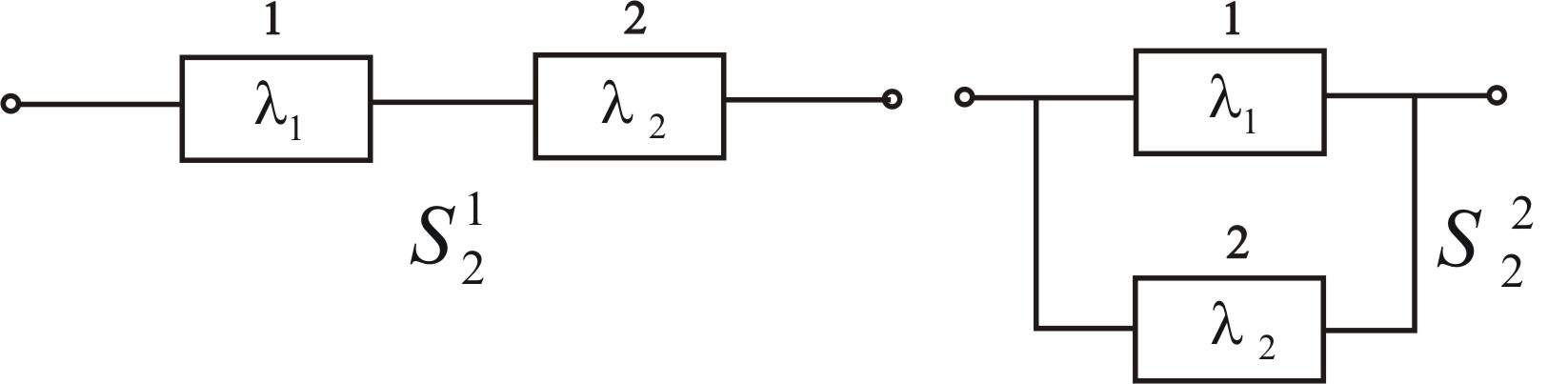
Рис. 3.50 – Примеры вариантов структуры S₂

Для структуры S₃ допустимы следующие 8 вариантов (рис. 3.51)

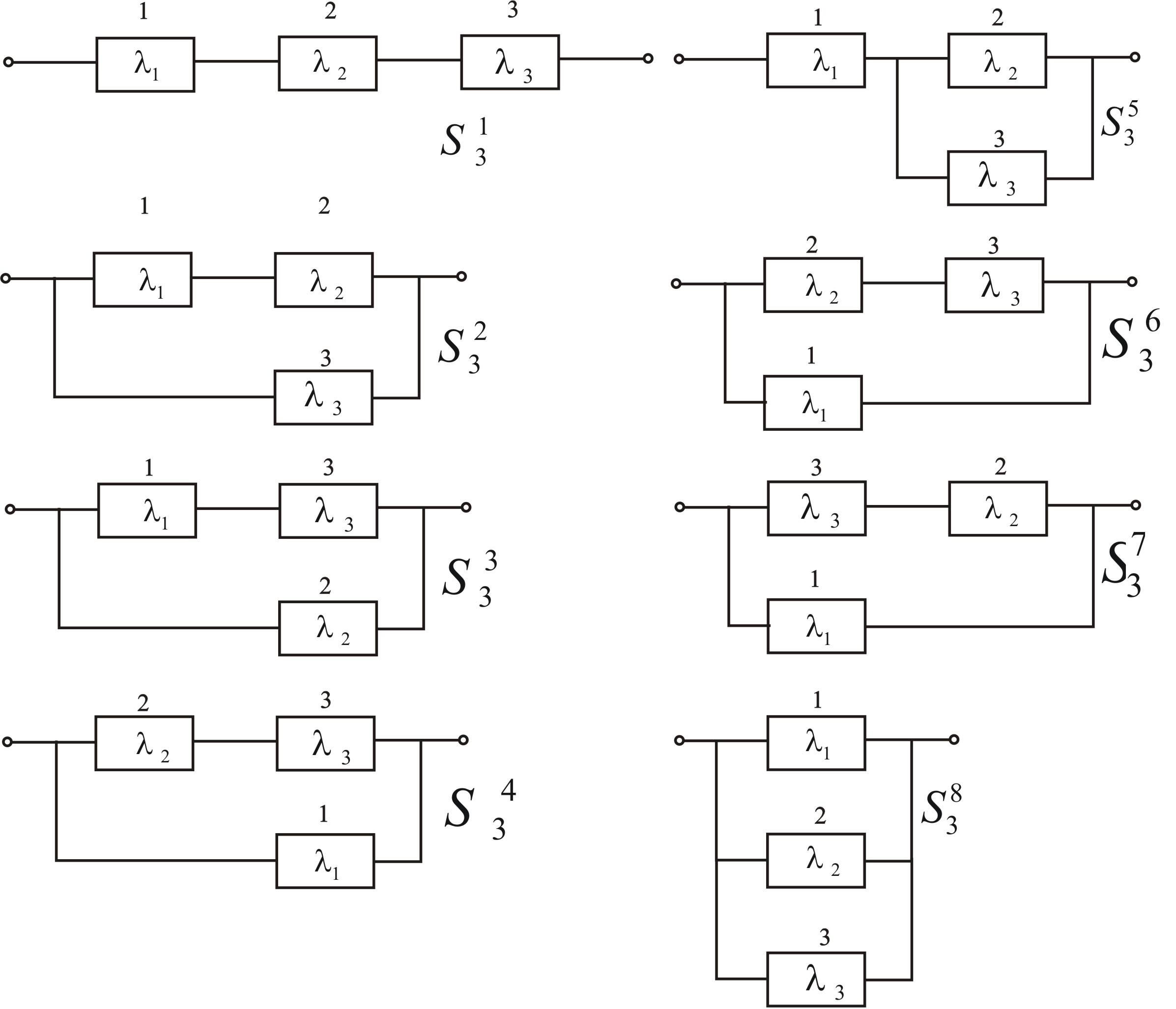
Рис. 3.51 – Примеры вариантов структуры S₃

Из этих примеров видно, что число возможных вариантов каждой структуры S_j очень быстро возрастает по мере увеличения её номера j. Подобный бурный рост размерности задачи синтеза затрудняет её решение уже при структурах из 6-8 элементов.

Для снижения размерности задачи синтеза следует искусственно ограничивать число d_j допустимых вариантов каждой структуры S_j. Делается это введением в условия задачи синтеза ряда ограничений, например, таких:

1. Задано число основных элементов;

2. Указана равнонадежность элементов;

3. Введено ограничение на стоимость всей системы.

В таком случае ограничение 1 «в синтезируемую систему входят 2 основных элемента» - оставляет для структуры S₂ только один вариант S₂¹;

для структуры S₃ оказываются возможными всего три варианта – S₃¹ , S₃², S₃⁵ (если за основные элементы принять например 1 и 2).

Ограничение 2: - «все элементы равнонадежны» - не влияет на число вариантов структур S₁, S₂ и резко снижает число вариантов d₃ до 4-х для структуры S₃ (рис. 3.52):

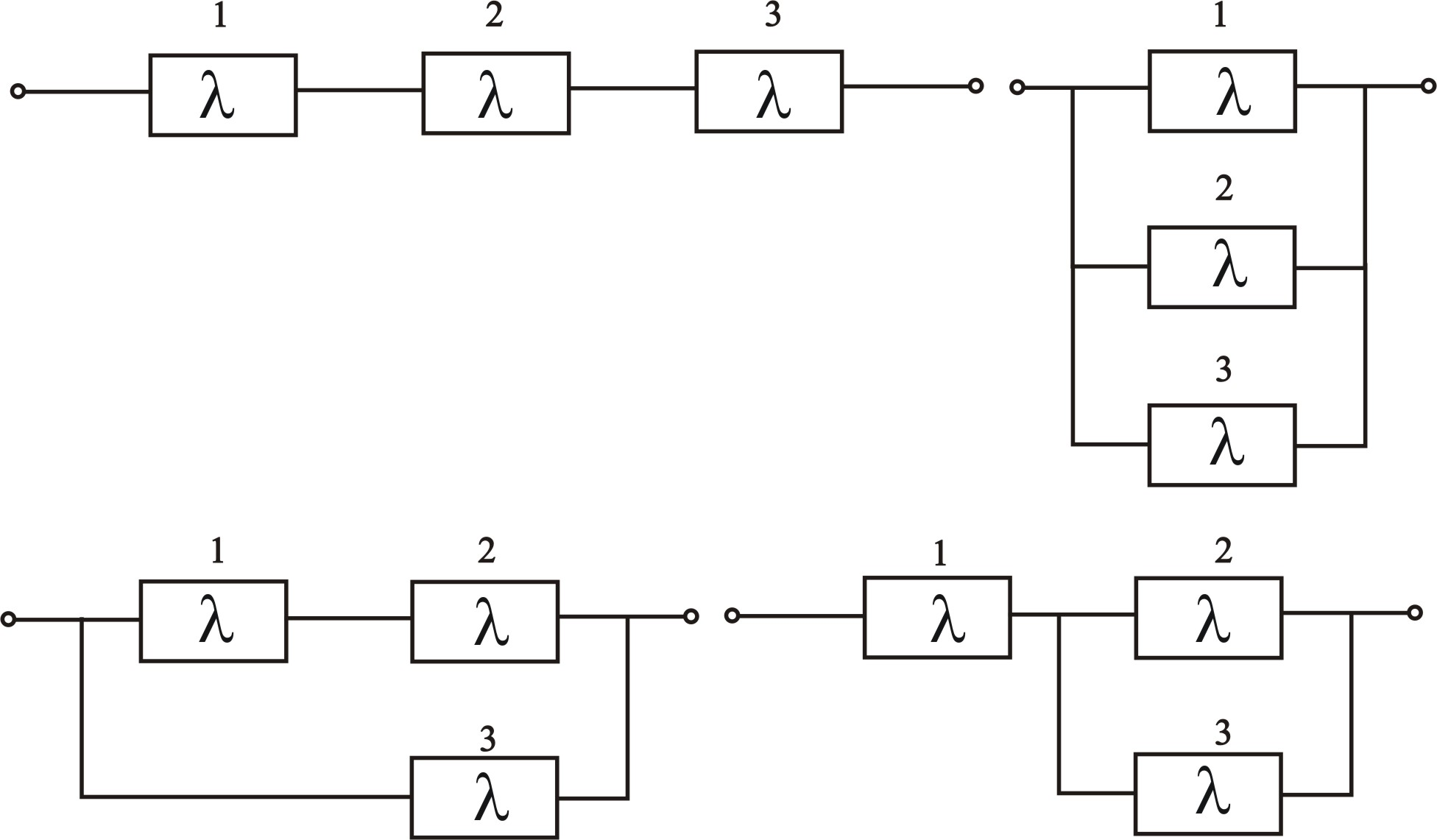
Рис. 3.52 – Примеры допустимых вариантов структуры S₃

Ограничение на стоимость синтезируемой системы эквивалентно уменьшению числа n используемых элементов с относительно малыми интенсивностями (напомним, что «дорогие» элементы обычно более надежны, а соответствующие интенсивности  - малы) или увеличение числа малонадежных элементов n с относительно большими интенсивностями .

При постановке задачи синтеза структура системы S рассматривается как лингвистическая переменная, принимающая дискретные «значения» S_j^h, j=1,2,…,n; h=1,2,…,d_j, которые заранее выписываются человеком-экспертом и используются для вычисления по соответствующим формулам значения критерия П(S_j^h) для каждого варианта S_j^h.

Понятие «отказ системы». Значения критерия П(S_j^h) зависят не только от структуры системы S_j или её варианта S_j^h, но и от используемого расширенного понятия «отказ системы». Так, например, для системы S₅ из пяти равнонадежных элементов с интенсивностью  под её отказом может пониматься случайное событие выхода из строя М элементов, М=1,2,3,4,5. Тогда из нижеприведенной табл. 10 видно, что изменение числа М с 1 по 5 изменяет среднюю наработку на отказ системы t_н^с более чем на порядок.

Таблица 10

Показатели надежности резервированной системы при расширенном понятии отказа

М	Pc	tнc
1	Р5	0.200
2	5p4-4p5	0.45
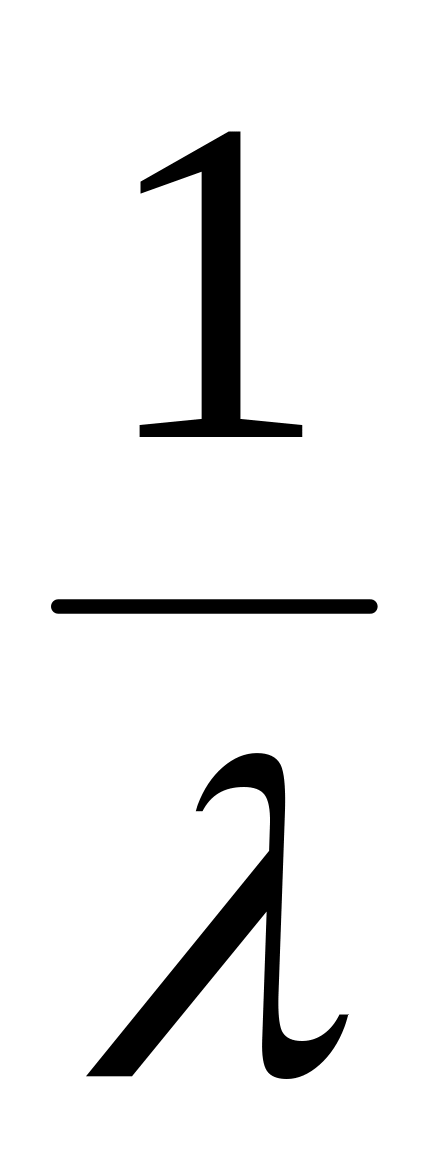
3	6p5-15p4+10p3
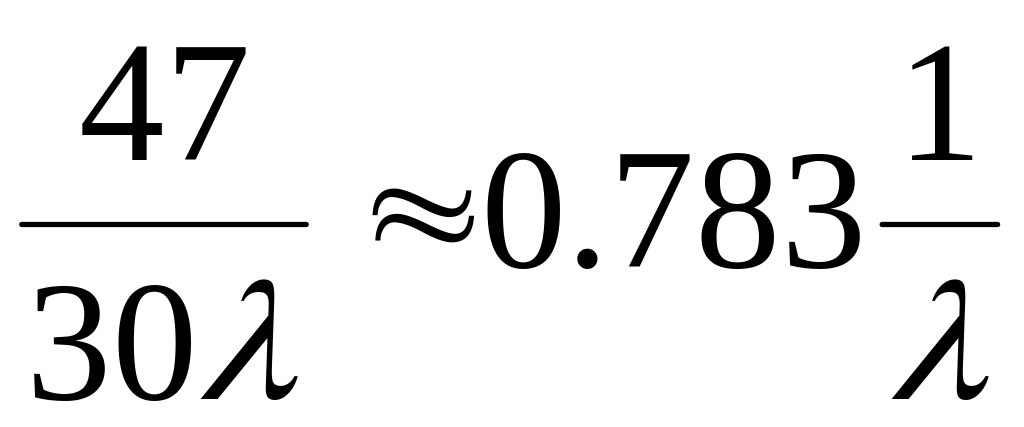
4	-4p5+15p4-20p3+10p2
5	1-(1-p)5

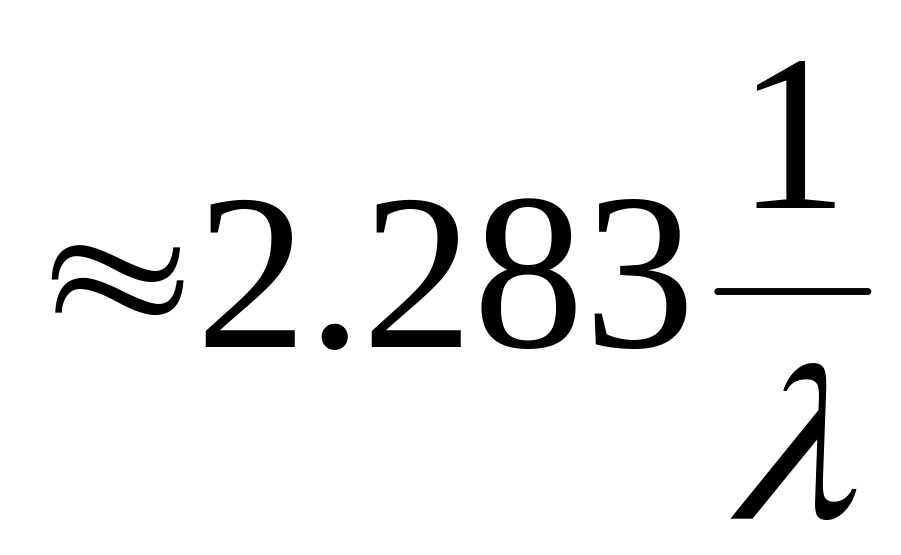
Строго говоря, понятие «отказ системы» относится к условиям (описанию) задачи синтеза и не является независимой переменной критерия П, т.е. не может изменяться в процессе синтеза системы. Вводя условное обозначение «отказ системы» - ОС в перечень аргументов критерия П(S, ОС, ), мы хотели подчеркнуть, что формулы для вычисления Р_с(t₀) и t_н^c существенно зависят от лингвистического определения «отказ системы».

Интенсивности отказов элементов . Значение критерия П, вычисляемого для каждого состояния системы S_j, зависит от вектор-функции интенсивностей

_j(t)={ ₁(t), ₂(t),…, _j(t)}

или, чаще всего, для экспоненциального распределения наработок до отказа, от числового вектора

_j={₁, ₂,…, _,…,_j}

При этом каждая компонента _ ограничена снизу и сверху

где - физически или экономически возможные минимальные и максимальные интенсивности отказов.

Интенсивность отказа можно при синтезе системы рассматривать как непрерывную независимую переменную из интервала .

В этом случае после синтеза системы с желаемым показателем надежности на векторе ^* возникает дополнительная задача конструирования или подбора элементов с интенсивностями отказов, равными оптимальным значениям . Эта дополнительная задача может оказаться весьма сложной и трудоемкой (особенно при малом числе элементов в системе), поэтому при синтезе системы удобнее рассматривать каждую _ как дискретную переменную, принимающую некоторые возможные значения

из интервала .

При этом каждый набор , соответствует существующей номенклатуре элементов с интенсивностями отказов . Обычно число k возможных значений (или номенклатурных вариантов одного элемента) невелико, k<3-5. Поэтому преобразование непрерывной переменной _ в дискретный аргумент несущественно усложняет общую задачу синтеза (напомним, что П(S_j^h) уже является дискретной функцией лингвистической переменной S), но заметно упрощает последующую реализацию синтезированной системы (и снижает её стоимость, так как при конструировании используются только серийные элементы).

Проведенный анализ задачи надежностного синтеза показывает целесообразность и необходимость рассмотрения критерия оптимальности Р_с(t₀) или t_н^с как кусочно-постоянной функции с разрывами I-го рода на множестве вариантов структур

S_j^h, j=1,2,…, n, h=1,2,…,d_j

и множестве дискрет _^, =1,2,…,j; ; =1,2,…,k

при неизменном понятии «отказ системы», определяющим формулы для вычисления П(S_j^h, _^).

Ограничения задачи синтеза. К ним относятся ограничения снизу и сверху на интенсивности _, структуры S_j и число целесообразных вариантов d_j:

где числа n⁺ и d_j⁺, j=1,2,… задается человеком-экспертом и указываются в условии (описании) задачи.

Одним из распространенных ограничений при надежностном синтезе систем является ограничение на их стоимость С_с. В первом приближении стоимость С_с прямо пропорциональна числу элементов, входящих в систему, и обратно пропорциональна интенсивностям отказов . Более того, во многих случаях С_са₁/^а2, где а₁, а₂ – эмпирические параметры, причем а₂2-3, т.е. уменьшение , например, в 2 раза вызывает увеличение стоимости в 4-10 раз.

Непосредственное использование в задаче надежностного синтеза стоимостного ограничения типа С_сС_с⁺, где С_с⁺ - допустимая стоимость системы, весьма затруднена существенной изменчивостью стоимостей отдельных элементов и всей системы в целом. Поэтому при синтезе системы из элементов с примерно близкими интенсивностями  более целесообразно говорить об ограничениях на сложность системы, понимая под сложностью число элементов или структуру S_j. Тогда система минимальной сложности (минимальной структуры), удовлетворяющая некоторым дополнительным требованиям, будет состоять из наименьшего числа элементов, а её стоимость будет, вероятно, достаточно близкой к минимальной стоимости.

Связями в задачах надежностного синтеза служат формулы для вычисления вероятности безотказной работы системы P_c(t) и средней наработки на отказ t_н^с, т.е. связи фактически включены в критерии оптимальности P_c(t₀) и t_н^с синтезируемой системы.

Ранее указывалось, что критерий П зависит от вариантов структуры S_j^h, вектора интенсивностей  и понятия отказа системы ОС, т.е. П=П(S_j^h, ,ОС).

Переменные  и ОС вводятся в условия задачи надежностного синтеза и не влияют на структуру формул П(S_j^h, ,ОС) (хотя, конечно,  и ОС влияют на значения П). Дискретная переменная S определяет число элементов в синтезируемой системе и их роль (основные или резервные) в каждом варианте структуры S_j^h, поэтому формулы для вычисления P_с(t) и t_н^с существенно зависят от S_j^h. Поэтому в общем виде связи следует записывать в таком виде

П=П_j^h(S_j^h, ,ОС), j=1,2,…,n, h=1,2,…,d.

Постановки задач надежностного синтеза

После анализа критериев оптимальности П={P_c(t₀), t_н^с}, независимых переменных , S, ОС, ограничений на , S и стоимость С_с, можно сформулировать две постановки задачи надежностного синтеза локальных (малоразмерных) технических систем.

Задача синтеза системы с экстремальными характеристиками надежности. Пусть указано целевое назначение синтезируемой простой системы и задан критерий оптимальности Р_с(t₀) или t_н^с. Кроме того, пусть четко сформулировано понятие «отказ системы», и заранее оговорены: максимально возможное число исходных элементов n⁺, их характеристики _j, , и, быть может, допустимая стоимость синтезируемой системы С_с⁺.

Требуется сконструировать из заданных элементов с интенсивностями _j, локальную систему, выполняющую целевое предназначение, и обладающую максимальной надежностью Р_с(t₀) (или t_н^с) при соблюдении ограничений

С_сС_с⁺, , , nn⁺.

Во многих задачах интенсивность отказов _j может принимать некоторые заранее заданные значения _j^, =1,2,…,k, k3-5. Тогда ограничения задачи синтеза преобразуются к виду:

С_сС_с⁺, , , nn⁺.

Первое и третье ограничения задачи синтеза существенно зависимы, ибо стоимость системы С_с в основном определяется числом её элементов n. Вместе с тем определение стоимости ещё не сконструированной системы, как правило, вызывает серьезные затруднения. Эти два обстоятельства, а также то, что решение задачи max P_c(t₀) может не удовлетворить конструктора системы, приводят к другой, практически более интересной постановке задачи надежностного синтеза.

Задача синтеза системы с заданными характеристиками надежности. Пусть сформулированы целевое назначение технической системы и понятие «отказ системы», а также заданы желаемые показатели надежности или . Кроме того, указаны показатели надежности элементов _j, и их допустимые значения , .

Требуется сконструировать из заданных элементов с интенсивностями _j, техническую систему минимальной сложности, выполняющую целевые назначения и обладающую показателями надежности

В этой задаче требование минимальной сложности означает минимизацию числа элементов n в синтезируемой системе, что, как правило, эквивалентно её наименьшей стоимости.

Очевидна двойственность приведенных задач надежностного синтеза. Критерий оптимальности первой задачи служит ограничением во второй задаче, а ограничение С_сС_с⁺ из первой задачи опосредованно превращается в критерий оптимальности синтезируемой системы во второй задаче. Подобная близость задач синтеза позволяет разрабатывать алгоритм решения какой-либо одной из задач на условный экстремум, в частности синтеза системы минимальной сложности с заданными показателями надежности.

Алгоритм надежностного синтеза локальной системы

Как и раньше, здесь под локальной системой понимается «малоразмерная» система, состоящая из небольшого числа n элементов (n6-8). Это условие позволяет построить относительно несложный алгоритм поиска условного экстремума целочисленного критерия n с дискретными ограничениями и связями. Алгоритм базируется на известных принципах «от простого – к сложному» и полного перебора возможных вариантов решения задачи.

Выпишем условие математической задачи синтеза. Заданы: критерий оптимальности n, являющийся натуральным числом n=1,2,…, n⁺; n⁺6-8;

- вектор интенсивностей отказов элементов

={₁, ₂, …, _j,…,_n+}, , k5-6,

_j^ - положительные числа, ,

- вектор возможных структур и вариантов системы , .

-желаемый уровень надежности синтезируемой системы

(или

Перед решением задачи синтеза составим таблицу формул (табл. 11), необходимых для вычисления показателя P_c(t₀) (и/или t_н^с) при заданном понятии «отказ системы».

Таблица 11

Структура	S1	S2	S3
Варианты	S11,…	S21,…,S22	S31,…,S3h,…, hd3
Формулы	П11,…	П21,…, П22	П31,…, П3h,…, hd3

Введем функцию невязки:

и условие окончания поиска приближенного решения

0, ₀, где ₀ – заданная допустимая погрешность, ₀0.

Алгоритм состоит из ряда последовательно выполняемых этапов.

Этап 1.

Задается самая простая для данной задачи структура S_j.

1. Для варианта ­­S_j¹ по формуле П_j¹ из табл. 11 находятся k значений P_c(t₀)_, =1,2,…,k для всех интенсивностей отказов элемента _j^, =1,2,…,k. Вычисляется k значений функции невязки _=P_c(t₀)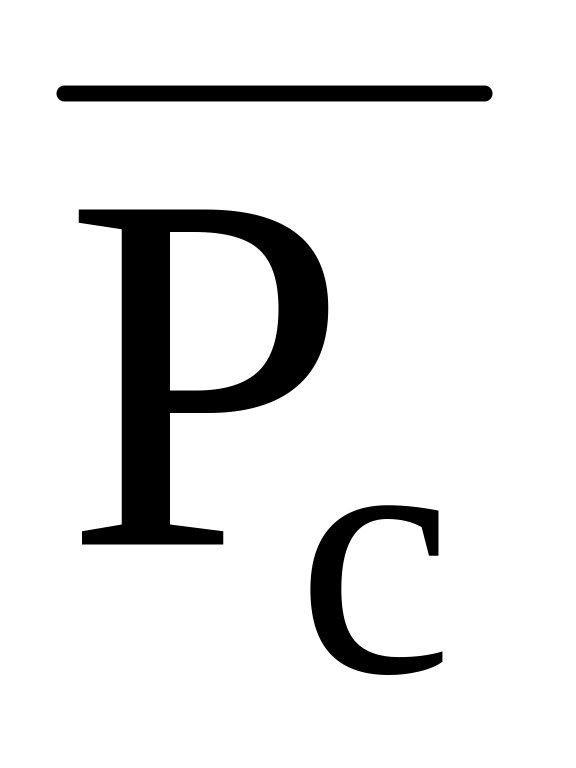_- , =1,2,…,k.

Для положительных _ проверяются условия «конца решения»:

а) если какое-либо _₀, то задача синтеза системы решена: найдена структура S_j¹ системы из минимального числа j равнонадежных элементов с интенсивностями отказов _j^, обеспечивающая желаемую надежность ;

б) если условие «конца» _₀ выполняется для нескольких , то за решение задачи принимается число j равнонадежных элементов с интенсивностью отказов _j^, где индекс  соответствует наименьшему положительному _..

в) если все _ отрицательны, =1,2,…,k, то:

для варианта S_j² повторяются все операции пункта 1 и либо находится решение задачи синтеза системы из j элементов, либо вводится вариант S_j³ структуры S_j и т.д. до тех пор , пока не будут проанализированы все k вариантов S_j.

Если структура S_j и все её варианты S_j^ не обеспечивают решения задачи синтеза, то осуществляется переход к следующей более сложной структуре S_j+1.

Этап 2.

Пусть задана структура S_j+1.

1. Для варианта S_j+1¹ по формуле П_j+1¹ (табл. 11) находятся k значений P_c(t₀)_, =1,2,…,k для всех _j+1^, =1,2,…,k.

Вычисляется k значений функции невязки _=P_c(t₀)_- , =1,2,…,k.

Для положительных _ проверяются условия «конца решения» и пункты а), б), в) и т.д., пока не найдется решение задачи синтеза среди структур S_j+1^, j=1,2,…,n⁺, или будет установлена после n⁺ этапов невозможность конструирования технической системы с желаемым (или ) из n⁺ равнонадежных элементов с интенсивностями отказов _j^, .

При отрицательном решении задачи синтеза следует пересмотреть заданные параметры n⁺, _j^, (n⁺ - в сторону увеличения, _j – в сторону уменьшения).

Целесообразно также обсудить с конструктором системы возможность уменьшения желаемого значения (или ).

3.4. Надежность сложной системы

Сложная (не простая!) система состоит из большого числа элементов с изменчивыми связями и переменной структурой. Такая система, как правило, многофункциональна и отказы отдельных элементов не вызывают отказа всей системы, но почти всегда влияют на полноту и качество выполнения некоторых её функций и, тем самым вызывают частичные отказы и снижение качества функционирования всей системы. Примером подобной сложной системы может служить АСУТП с централизованной и, особенно распределенной структурами, а также многие информационно-вычислительные системы реального времени.

Главная особенность сложной системы – невозможность или затруднительность строгой объективной формулировки понятий «работоспособность» и «отказ», что, в свою очередь, делает невозможным применение введенных ранее функциональных и числовых показателей надежности Q(t), P(t), f(t), (t), t_н, t_, к_г, к_ог для описания поведения случайных величин: наработки Т и длительности восстановления Т^в.

В связи с этим появляется необходимость введения новых функциональных и числовых характеристик надежности сложной системы, базирующихся на понятии эффективности функционирования системы.

Модель функционирования сложной системы.

Пусть сложная система состоит из m восстановливаемых элементов, часть из которых может быть основными, а часть – резервными. При этом каждый элемент может находиться в состоянии работоспособности или отказа (восстановления); переходы из одного состояния в другое происходят мгновенно (рис. 3.53)

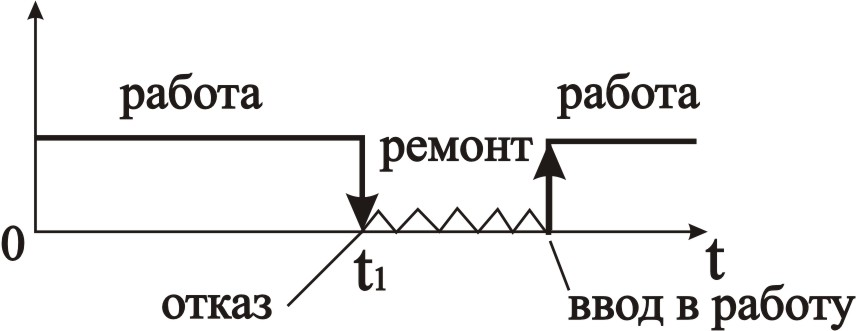
Рис. 3.53 – Схема функционирования элемента сложной системы

Присвоим каждому элементу системы индекс (имя) , =1,2,..., m.

В каждый момент времени t система находится в некотором техническом состоянии S_i, i=1,2,…,M, однозначно определяемом числом и номерами отказавших элементов. Например, в состоянии S₁ все m элементов системы исправны; в состоянии S₂ – отказал один элемент с номером =1 (все остальные исправны); в состоянии S₃ – отказал один элемент с номером =2 (остальные m-1 элемента работоспособны);при выходе из строя элементов с =1 и =2 возникает состояние S_m+2 и т.д.

Наконец, в состоянии S_M отказали все m элементов (состояние полной неработоспособности). Можно подсчитать общее число М=2^m разных состояний системы S_i, .

В процессе функционирования система мгновенно переходит из произвольного состояния S_i, в любое другое состояние S_j, вследствии отказов тех или иных элементов и/или ввода их в работу после окончания ремонта. Эти события – отказ и восстановление – происходят в случайные моменты времени, поэтому, считая потоки отказов и восстановлений простейшими, смену состояний можно описать случайным марковским процессом с непрерывным временем t и дискретными состояниями S_i, (рис. 3.54).

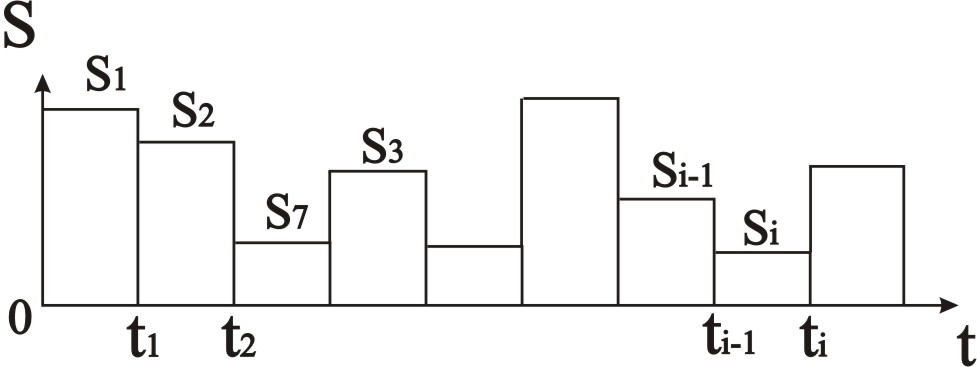
Рис 3.54 – График смены состояний сложной системы

Для марковского процесса переход из состояния S_i в состояние S_j определяется одним числовым параметром – интенсивностью перехода . В общем случае .

Интенсивности перехода _{i, j} определяются интенсивностями отказов и восстановлений отдельных элементов системы,

Для удобства описания введем конечномерный вектор состояния системы , а также векторы интенсивностей отказов и восстановлений элементов , вектор интенсивностей переходов системы . При этом вектор =(, ), а вектор состояний системы S=S()=S(, ).

Эффективность функционирования сложной системы.

Любая сложная система создается для достижения той или иной цели. Способность (свойство) сложной системы достигать своей цели называют её эффективностью. Степень эффективности или количественная близость к поставленной цели характеризуют некоторой количественной мерой – критерием эффективности I.

Каждая цель в общем случае может описываться набором частных критериев качества . Используя известные методы преобразования векторных критериев к скалярным мы можем свести к одному обобщенному критерию эффективности I.

При анализе сложных автоматизированных систем в качестве критерия эффективности обычно принимают следующие показатели:

• технико-экономические (прибыль, себестоимость, эксплуатационные затраты и др.);

• технологические (производительность, КПД, степень превращения вещества и т.д.)

• информационные (время ожидания в очередях на обработку информации, вероятность решения задачи за заданное время, средняя скорость переработки информации и др.).

Отметим, что два первых типа критериев эффективности относятся к замкнутой системе «ТОУ - АСУ», третий критерий характеризует в основном АСУ или информационно-вычислительную систему.

Различают «мгновенную» эффективность сложной системы в любой момент времени t₀, оцениваемую значением критерия I(t₀), и усредненную эффективность функционирования сложной системы на заданном отрезке времени [0, T₀]

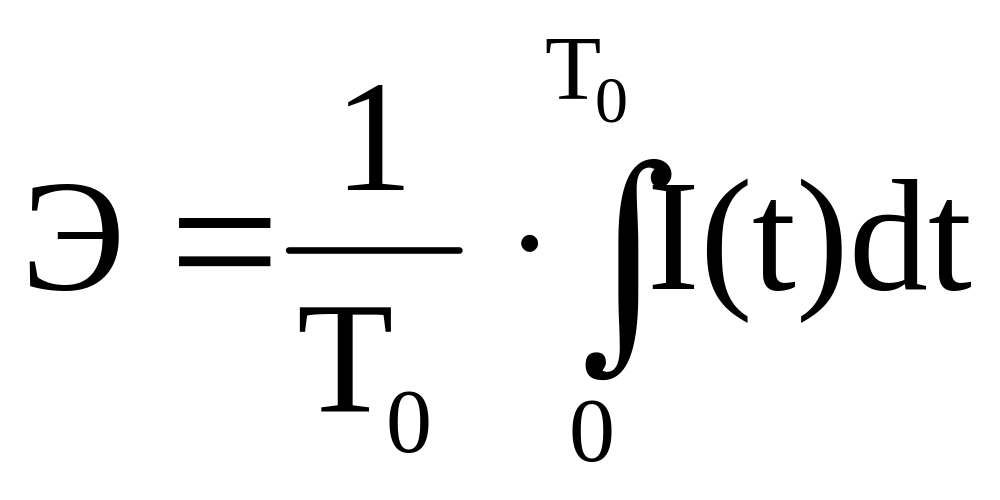
где T₀ – директивное время, например, горизонт планирования работы системы (квартал, декада, год и т.д.).

Критерии I и Э зависят от состояния системы S(t) в момент времени t, и режима работы R(t) системы в каждом из возможных состояний S_i, то есть

Э=Э(S(t), R(t))

Для упрощения задачи анализа эффективности будем полагать, что состояние S_i не зависит от режимов функционирования системы во всех предшествующих состояниях. Кроме того, пусть для каждого состояния S_i заранее известен расчетный (номинальный) или оптимальный режим функционирования системы R_i, , который «мгновенно» устанавливается при возникновении S_i. При этом режим R_i обеспечивает в состоянии S_i расчетное (номинальное) или оптимальное значение критерия I_i. Итак, имеем «цепочку» (рис. 3.55)

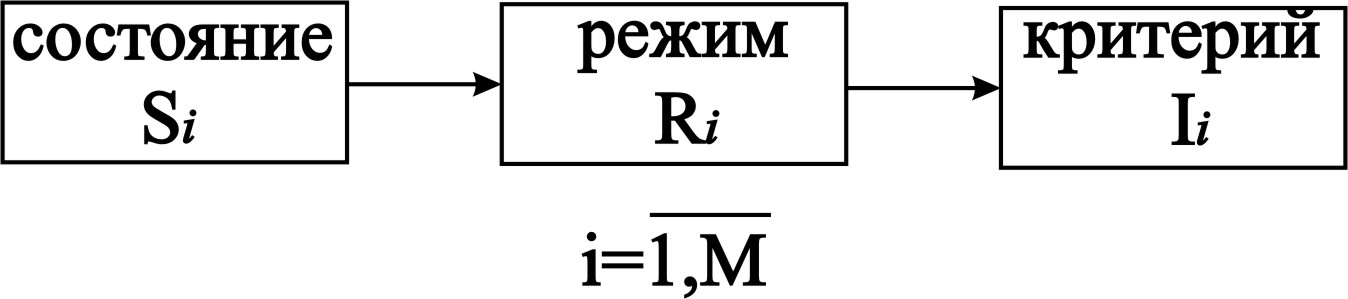
Рис. 3.55 – К расчету критериев качества I_i

При сделанных допущениях оказывается, что средняя эффективность Э зависит только от состояний S_i, , возникающих в случайные моменты времени t на интервале [0, T₀]:

Э=Э(S(t)),

То есть, эффективность опосредственно определяется безотказностью и ремонтопригодностью всех элементов системы

Э=Э(S(, , t)),

где ,  - векторы интенсивностей отказов элементов .

Уточним теперь понятие эффективности. Назовем технической эффективностью свойство сложной системы достигать своей цели при учете потоков отказов и восстановлений её элементов и соответствующего ремонтного персонала. Соответственно показатель Э(S(, , t)) будет называться критерием технической эффективности сложной системы.

Так как для заданной системы значение критерия Э однозначно определяется надежностными характеристиками ,  всех элементов, то Э(S(, , t)) является количественной мерой надежности сложной системы, не имеющей формализованных понятий «работоспособность» и «отказ».

По смыслу критерия технической эффективности его максимальное значение достигается в состоянии S₁, когда исправны все элементы, а минимальное – в состоянии S_м, когда отказали все m элементов (рис. 3.56).

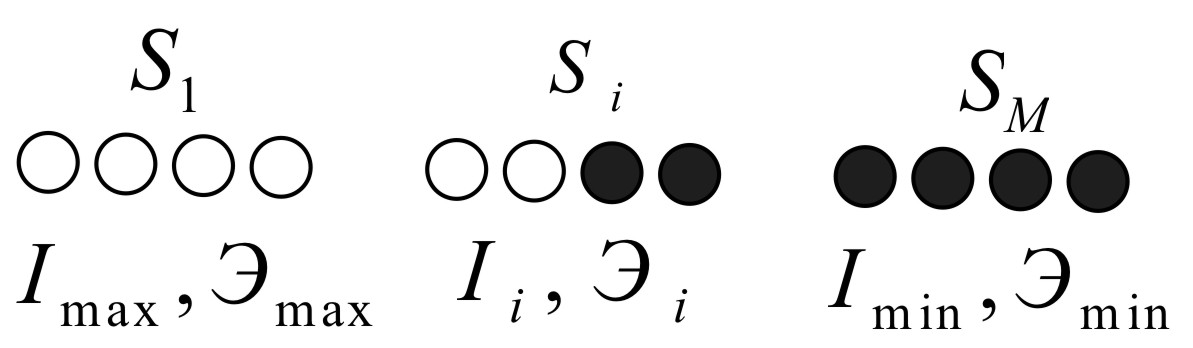
Рис. 3.56 – К определению минимального и максимального значения критериев качества I_i и эффективности : ○ – исправный элемент, ● – отказавший элемент

При любом произвольном S_i, i1, iM, критерий Э(S_i)=Э_i удовлетворяет нестрогому неравенству

, i=2, 3, … , M-1.

Остаётся получить формулу для вычисления критерия Э(S).

В произвольный момент t, система случайным образом оказывается в одном из состояний S_i, , а её мгновенная эффективность I принимает значение I_i. Обозначим вероятность нахождения системы в момент t в состоянии S_i через P_i(t), . Так как мгновенная эффективность I в момент t является дискретной случайной величиной, принимающей значения I₁, I₂,…, I_M, то её математическое ожидание или истинное среднее равно:

Далее легко определить среднюю техническую эффективность

Для вычисления Э требуется знание вероятностей P_i(t), .

Определение вероятностей состояния системы.

При известных интенсивностях _ij, _ji переходов системы из состояния S_i в любое другое состояние S_j, и обратно из S_j в S_i вероятности Р_i нахождения сложной системы в состоянии S_i, находятся как решения линейных дифференциальных уравнений Колмогорова

где в общем случае _ij_ji.

Сложная система всегда находится в одном из M состояний, поэтому для любого t и число дифференциальных уравнений можно уменьшить на единицу (для сложной системы M=2^m и число уравнений достигает нескольких сотен и тысяч).

Для решения системы уравнений надо задать M (или, точнее M-1) начальных условий P_i(0). Если считать, что система включается полностью исправной, то

P₁(0)=1, P_i(0)=0, .

Системы линейных дифференциальных уравнений высокой размерности целесообразно решать численно, используя для этого известные методы интегрирования, например, Рунге-Кутта 4-го порядка, или более точные явные и неявные методы Адамса с автоматическим выбором шага интегрирования.

При больших значениях времени t производные dP_i/dt становятся малыми и тогда дифференциальные уравнения можно заменить на линейные алгебраические

где - стационарная вероятность нахождения системы в состоянии S_i.

Так как в правую часть этого уравнения не входит , то оно разрешается относительно вероятности :

Анализ задачи оценивания технической эффективности.

Знание вероятностей P_i(t) и позволяет вычислить среднюю техническую эффективность системы:

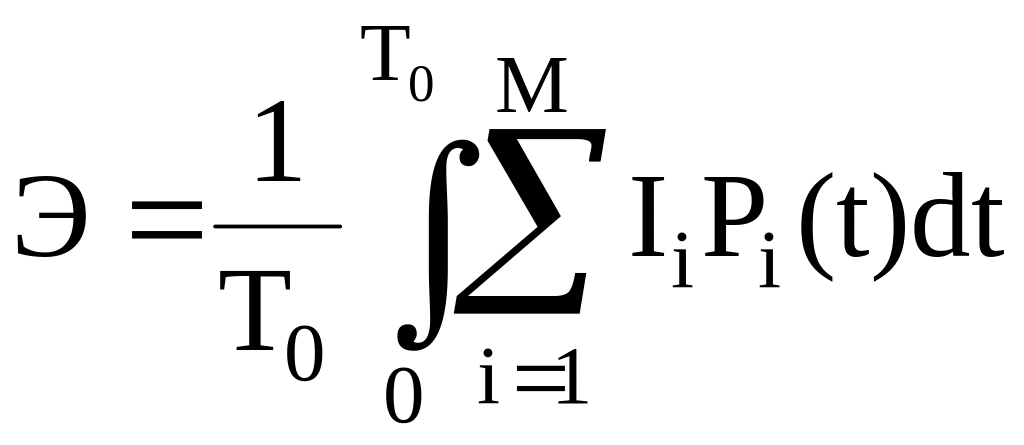
и для стационарного режима системы

Критерии Э и имеют физическую размерность целевой функции I, что затрудняет сравнение эффективностей разных сложных систем с неоднородными показателями качества работы. В таких случаях удобно использовать безразмерный критерий технической эффективности:

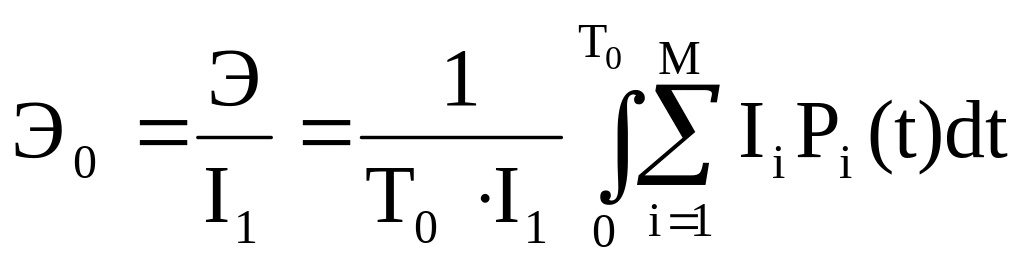
или для стационарного режима

Эти критерии изменяются в интервале от 0 до 1 (здесь принято, что в состоянии S_M имеем I_M=0, а в состоянии S₁ вероятности P₁(t) и по договоренности равны 1, так как все m элементов системы работоспособны).

Из анализа задачи можно сделать ряд очевидных заключений:

1. Чем ближе к единице, тем более эффективна техническая

система, тем выше её надежность и ремонтопригодность в целом.

2. Если возможны r вариантов построения одной и той же сложной

системы из одних и тех же m элементов, и для каждого известны , =1, 2, ... , r, то с позиции надежности наиболее предпочтителен вариант с наибольшим значением .

3. Если для решения некоторой проблемы создается несколько, например, две разные системы из разных элементов, и для них определены 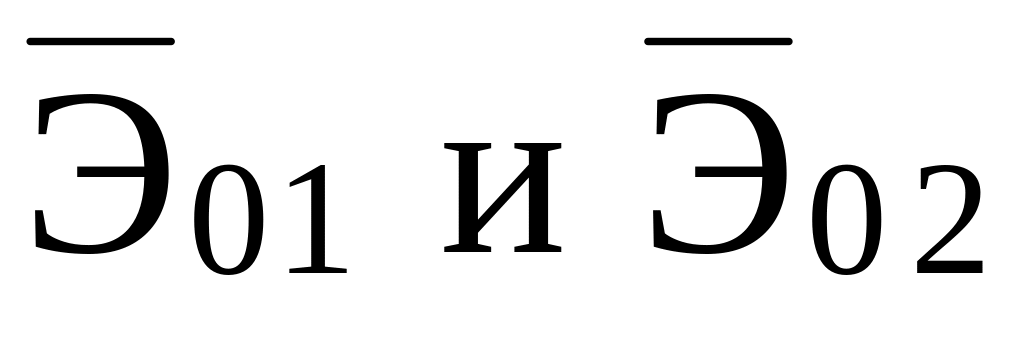, причем 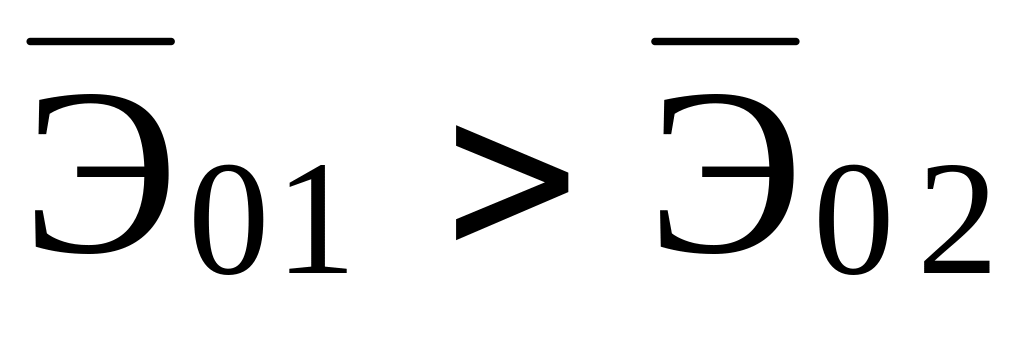, то с позиции надежности более выгодна система 1 с наибольшим значением критерия технической эффективности.

4. Если для двух разных систем соответствующие критерии ,

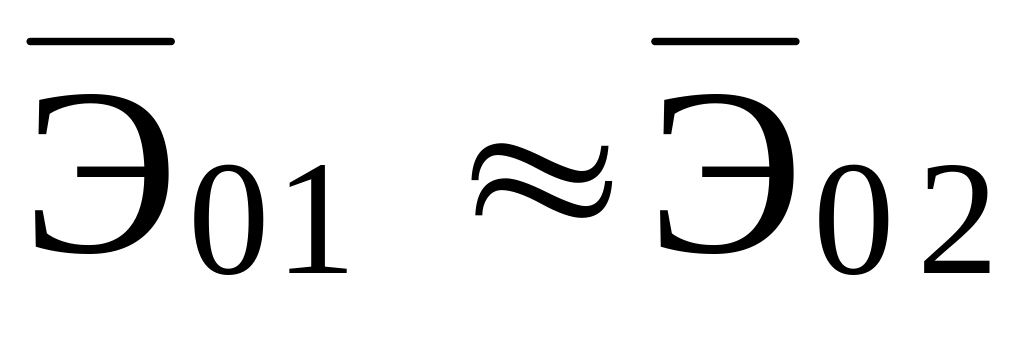то целесообразно применять систему с наименьшей стоимостью изготовления и эксплуатации.

Анализ размерности задачи оценивания технической эффективности

Под размерностью задачи будем понимать число M возможных состояний системы, которое определяет число различных значений критерия I_i, , и вероятностей P_i(t) или , .

Число M состояний системы S_i существенно зависит от количества m входящих в нее элементов M=2^m (табл. 12).

Число элементов m	2	3	4	5	6	7	8	10	12	14	16
Число состояний М	4	8	16	32	64	128	256	1024	4098	16392	65536

Таблица 12

Зависимость числа состояний системы М от числа элементов m

Проанализируем в качестве примера трудоемкость задачи для m=16 ( система из 16 элементов – это «небольшая» система типа АСУТП). Для оценки технической эффективности системы из 16 элементов надо:

Знать: - критерий I,

• вектор интенсивности отказов ={₁, ₂, … , ₁₆};

• вектор интенсивности восстановления ={₁, ₂, … , ₁₆};

Определить:

• элементы матрицы интенсивностей переходов, размерностью 6553665536;

• значения критерия эффективности I₁, I₂, … , I_i, … , I₆₅₅₃₆ (для этого 65536 раз выполняется расчет номинального режима или 65536 раз решается задача оптимизации I_i);

• функции P₁(t), P₂(t), … , P₆₅₅₃₆ (для этого численно интегрируется система из 65536 дифференциальных уравнений);

• значение Э₀ (находится с помощью квадратурных формул трапеций или прямоугольников).

Понятно, что даже при таком относительно малом m трудоемкость оценивания технической системы оказывается чрезвычайно высокой, а при увеличении m до 100 и более определение Э₀ рассмотренным методом становиться невозможным.

Высокая размерность задачи оценивания эффективности сложной системы негативно влияет и на свойства критерия , наиболее часто используемого при анализе и синтезе систем. Этот критерий представляет собой ограниченную кусочно-постоянную функцию 2m дискретных интенсивностей и способа соединения между собой элементов (структур и вариантов систем). Такая высокая размерность функции делает её малочувствительной к изменению состояний S_i, , что заметно затрудняет решение оптимизационных задач синтеза сложных систем.

При фиксированном состоянии S_i критерий в общем случае зависит от значения функционала I­_I(x, y), который в свою очередь определяется режимными входными и выходными координатами X(t), Y(t). В состав вектора X(t) входят нагрузка, возмущения и управление. Обычно, при функционировании системы в номинальном («расчетном») и/или оптимальном режиме критерий I_i слабовыпуклый и имеет малую норму градиента . Слабая чувствительность I_i по переменным x, y позволяет считать критерий технической эффективности почти независимым или слабозависимым от режима функционирования системы в каждом состоянии S_i, и использовать при расчете Э₀ заранее рассчитанные значения I_i для номинальных режимов.

Понижение размерности задачи оценивания эффективности

Для понижения размерности задачи оценивания эффективности сложной системы следует уменьшать число М её возможных состояний S_i, . Сделать это можно разными способами, в частности, путем «укрупнения» элементов и уменьшения их числа m.

Метод «крупных» элементов – блоков. Для некоторых сложных систем (типа АСУТП, информационно-вычислительных систем и др.) можно ввести новые, более «крупные» элементы – блоки, объединяющие ряд исходных основных элементов. Для простейших потоков отказов и восстановлений элементов интенсивности отказов и восстановлений блоков находятся по известным формулам

где к – число основных элементов с интенсивностями , включенных в один блок.

Среднее число блоков равно отношению , поэтому при k3-8 размерность задачи оценивания эффективности существенно снижается. Так, например, в системе из 20 исходных элементов возможны 2²⁰ =1 048 576 состояний. Если удастся создать блоки из k=5 элементов, то число блоков окажется равным четырем и количество «блочных» состояний станет равно 2⁴=16, следовательно размерность задачи снизится в раза.

Даже создание 10 блоков по 2 элемента каждый позволяет получить 2¹⁰ = 1024 “блочных” состояния и снизить размерность задачи оценивания эффективности в раза.

Метод критериальных состояний. Понижение размерности задачи здесь достигается за счет введения нового понятия состояние системы, что обеспечивает значительное (в 10-100 раз), уменьшение числа М состояний. Так, если известен диапазон (шкала) изменения критерия I(S, R) сложной системы, то можно выделить несколько непересекающихся поддиапазонов I₁, I₂,…, I_, …, I_d, d<<M и рассматривать d новых критериальных состояний.

Под критериальным состоянием S_ понимается такая структура сложной системы и режим работы её элементов, при которых значение критерия I_ I_, . В частности, при анализе эффективности распределенных АСУТП рекомендуется вводить 3 или 4 подинтервала: оптимальный и/или нормальный (номинальный), резервный и аварийный. Понятно, что при столь малых числах d проблема размерности задачи становится неактуальной: вычисление вероятностей критериальных состояний Р_ и значений I_ не вызывает затруднений . Однако при этом возникает дополнительная задача выявления связей между каждым техническим «элементным» состоянием S_j, и критериальным состоянием S_^k, (рис. 3.57).

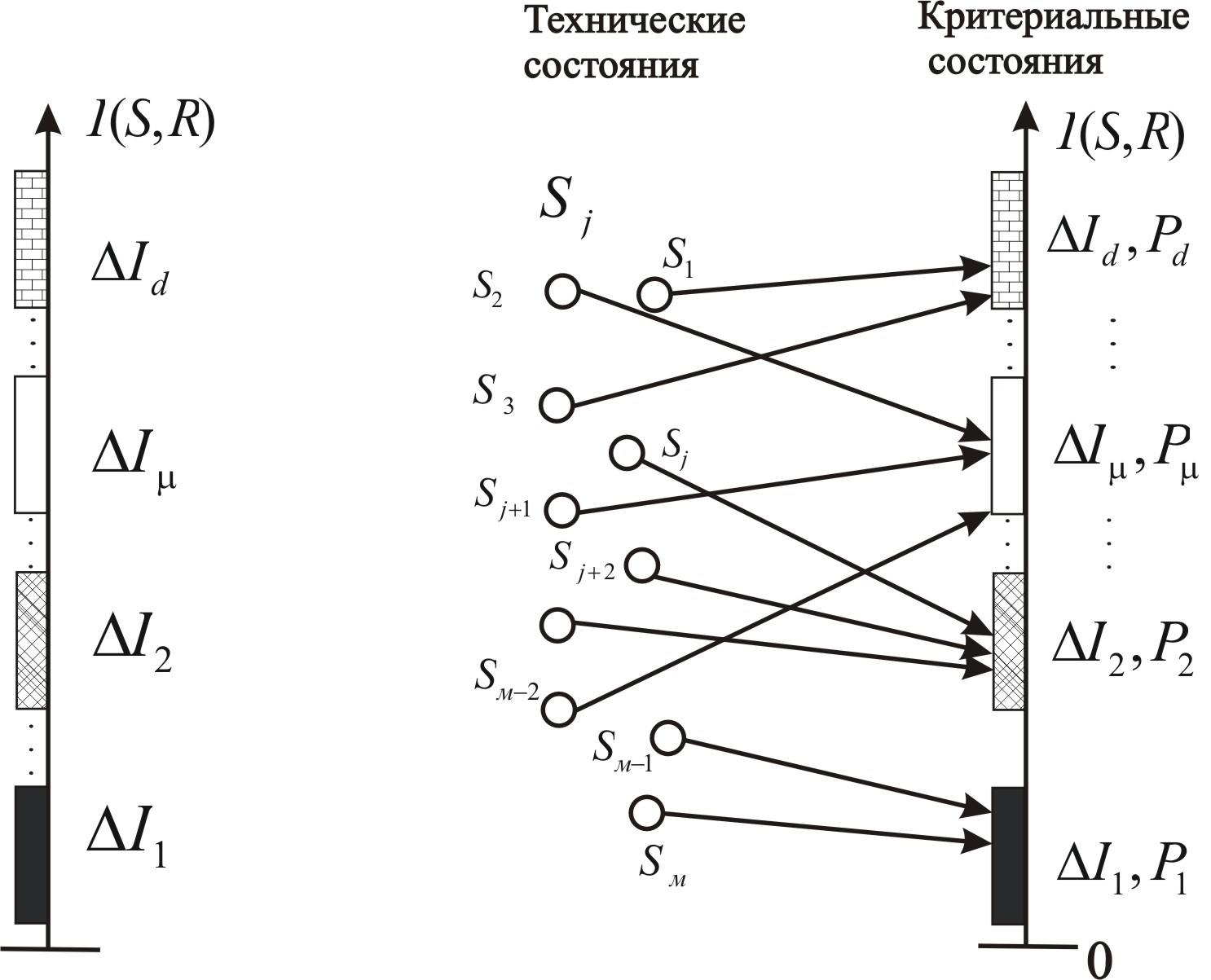
Рис. 3.57 – К понятию критериального состояния сложной системы

Метод функциональных состояний. Применяется при анализе эффективности сложных систем с четко указанными функциями (например, АСУТП с централизованной и распределенной технической структурой).

Предположим, что сложная система из m элементов выполняет l функций, l<<m, т.е. l в 10-100 раз меньше m. Пусть известны все элементы системы, реализующие каждую j-ю функцию, j=1,2,…, l и образующие при этом некоторую простую подсистему с формализованными понятиями работоспособности и отказа. Тогда можно ввести понятие функционального состояния системы h_j, однозначно определяемого числом и номерами отказавших функций. Общее число М_ф функциональных состояний системы равно 2^l.

При l<m и l<<m число функциональных состояний заметно уменьшается относительно числа М. Так, если l<0.5*m, то М_ф<<М. Например, при m=20 имеем М=1048576, l=0.5∙20=10, М_ф=2¹⁰=1024; тогда , следовательно число состояний системы уменьшилось в 65536 раз.

Как и методе критериальных состояний, здесь возникает дополнительная (причем достаточно сложная) задача выявления связей между состоянием каждого элемента или техническим «элементным» состоянием S_i, и функциональным состоянием S_ф (рис. 3.58).

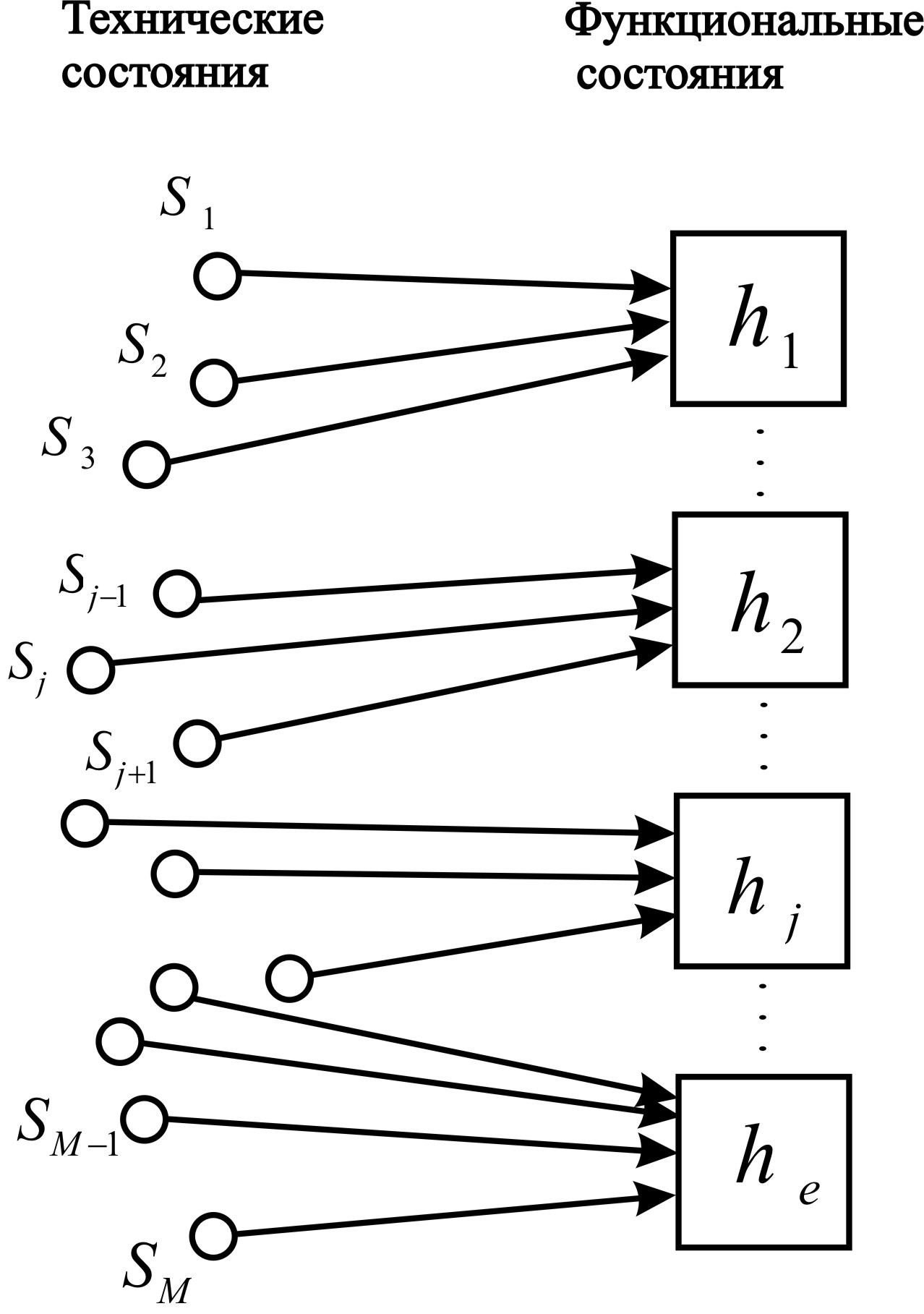
Рис. 3.58 – К понятию функционального состояния сложной системы

Помимо рассмотренных выше методов существуют еще несколько приемов уменьшения размерности задачи оценивания эффективности сложных систем, заключающиеся в объединении ряда элементов в небольшое число групп по тем или иным признакам, в частности по значениям стационарных вероятностей и введении понятия группового состояния системы S_^г, =1,2, …, к_г. Число групп обычно на порядок меньше числа технических элементов m, что существенно (на 2-3 порядка) уменьшает число групповых состояний и снижает трудоемкость определения . Вместе с тем использование групповых состояний S_^г влияет на точность вычисления (чем меньше групп, тем больше погрешность определения ) и требует выявления связей между каждым элементным состоянием S_i, и групповым состоянием S_^г, .