Работа с функциями.
Встроенные функции задаются именем и значением аргумента в круглых скобках. Аргумент может быть действительным или комплексным числом. В MathCAD существуют встроенные тригонометрические, гиперболические, показательные, логарифмические, статистические и др. функции. Для выбора функции на стандартной панели инструментов есть кнопка f(x). Появляется диалоговое окно, аналогичное окну функций в программе Excel.
Следует отметить, что принцип разбиения функций по группам или категориям в некоторых случаях представляется спорным. Поэтому при выборе функции полезно обращать внимание на поле с названием функции и краткую справку по выбранной функции. При этом следует иметь в виду, что очень часто встроенные функции MathCAD, по сравнению с их математическими двойниками, имеют некоторые особенности определения (например, ограниченная область определения и т.п.).
В MathCAD можно создать функции пользователя, если необходимо многократно вычислять одно и то же выражение. Чтобы определить функцию пользователя, необходимо ввести ее название, а в скобках после названия указать аргумент или аргументы через запятую. После этого вводится оператор присваивания и выражение, которым задается функция. В выражении для функции должны присутствовать аргументы функции, а также могут быть другие переменные, которые следует предварительно инициализировать. Все величины из правой части функции должны быть заданы левее и выше задания функции пользователя. Чтобы узнать значение функции для какого-либо конкретного значения аргумента, функция вызывается с этим значением аргумента и после нее указывается знак равенства.
Работа с векторами и матрицами.
Векторизация – одновременное проведение некоторой скалярной математической операции над всеми элементами вектора или матрицы. Т.е. векторизация позволяет применять скалярные операторы и функции к массивам. Обозначается стрелкой над названием массива или операции. Операция задается с панели инструментов Matrix после написания имени массива или выражения с использованием массива (или массивов).
По отношению к векторам и матрицам могут применяться арифметические операторы (сложение, вычитание, деление и умножение) и операторы с панели инструментов Matrix (транспонирование, детерминант, выделение столбца, обращение матрицы). Естественно при этом массивы должны удовлетворять определенным условиям, например, при сложении и вычитании иметь одинаковую размерность и размер, при умножении число столбцов первого массива должно быть равно числу строк второго массива, к квадратным матрицам применима операция возведения в степень.
Иногда необходимо производить какие-либо действия только с одним (несколькими) столбцами или строками матрицы. Чтобы выделить из матрицы столбец существует оператор на панели инструментов Matrix М<>. Если необходимо выделить строку, то сначала матрицу транспонируют, а затем из полученной матрицы выделяют строку. Результат в этом случае будет вектором-столбцом. Если нужно получить вектор-строку, то опять выполняют транспонирование.
В матрицу можно добавлять (удалять) строки или столбцы. Для этого выделяют элемент матрицы (ставят после него курсор). Строки будут добавляться сразу под строкой с этим элементом, а столбцы добавляются справа от столбца с выделенным элементом. Затем выбирают команду Insert-Matrix и в открывшемся диалоговом окне указывают число добавляемых (или удаляемых) строк и столбцов. Далее нажимают клавишу Insert (или Delete)
В MathCAD существует ряд функций для создания и матриц и вычисления их характеристик, функция для поиска минимальных и максимальных элементов массивов, выделения действительных и мнимых частей элементов матрицы.
Очень часто новая матрица создается путем объединения уже существующих. Функцией stack(M1,M2,…) матрицы М1 и М2 добавляются одна к другой снизу (матрица-аргументы функции должны иметь одинаковое число столбцов), функцией augment(M1,M2,…) матрицы М1 и М2 объединяются слева направо (матрицы-аргументы должны иметь одинаковое число строк), функция submatrix(M1,ir,jr,ic,jc) выделяет из матрицы М1 строки от ir до jr и столбцы от ic до jc.
Решение уравнений
Функции для решения уравнений.
(Очков) Собака после выстрела и команды «Искать!» может вернуться к охотнику с тремя результатами:
1) собака приносит подстреленную дичь;
2) собака, израсходовав отпущенный лимит времени или услышав призывной сигнал охотника, возвращается с пустыми руками, пардон, зубами;
3) охотник получает «трофей» — стреляный пыж или рваный башмак, но собачьи глаза и собачий хвост выдают собачью хитрость.
Поиск решения с помощью функций root, Find и Minerr во многом напоминает ружейную охоту. Пользователь формирует анализируемую функцию, вводит ограничения, выставляет параметры поиска (заряжает ружье, выслеживает дичь), а затем нажимает клавишу F9 (спусковой крючок ружья). «Собака» (среда MathCAD) «прыгает в воду» и возвращается с тремя результатами:
1) решение найдено (см. пункт 3 рис. 3.1);
2) решения не найдено (см. пункт 4);
3) MathCAD пытается подсунуть пользователю что-то такое, что только издали напоминает правильный результат (см. пункт 5).
При этом ситуация осложняется еще и тем, что пользователь MathCAD в отличие от охотника, который знает, что такое дичь, часто не имеет понятия о том, что такое правильный результат. У среды MathCAD, к сожалению, нет глаз и хвоста, по которым можно определить, что принесено к ногам охотника — пользователя пакета.
Работа с функциями root, Find и Minerr — это хождение на охоту с чужой собакой, повадки которой неизвестны. «Своя собака» — это методы и алгоритмы, написанные на языке MathCAD и вставленные в документ, по которым решение ищется не вслепую, а наверняка.
А если писать программы недосуг, то вот семь советов по работе с функциями root, Find и Minerr :
1) найдя решение, еще раз заставьте MathCAD найти его уже от новой опорной точки;
2) перед решением оптимизационной задачи с ограничениями прогоните ее не с функцией Minerr , а с функцией Find для того, чтобы оценить область существования решений;
3) начинайте поиск оптимального решения от одной из точек, найденной в пункте 2 и лежащей недалеко от оптимума;
4) вводите ограничения постепенно: ввели первое - нашли решение, ввели второе - уточнили его и т.д.;
5) начинайте решение оптимизационной задачи с целочисленными аргументами без ограничений на целочисленность. Нецелочисленный ответ всегда будет полезен, так как 1) от него можно начать поиск целочисленного решения, 2) можно удовлетвориться нецелочисленным решением (появление совместителя, например, в задаче об оптимальном штатном расписании) и 3) числа можно округлить вручную, если целочисленное решение не находится;
6) проверяйте правильность найденных корней, минимумов и максимумов построением графиков и поверхностей, где эти точки видны, благо пакет MathCAD имеет богатый набор графики, средств визуализации зависимостей. Если аргументов у функции больше двух, то постройте графики сечений через точку оптимума по всем координатам и убедитесь, что там все частные производные равны нулю;
7) имейте набор пользовательских функций для решения конкретных задач не лобовой атакой через встроенные функции, а более осмысленными способами. Подобные функции-программы приведены в этюде 6.
Решение систем линейных алгебраических уравнений.
Система таких уравнений в матричной форме имеет вид A*X=B, где A – матрица коэффициентов при неизвестных, X – вектор неизвестных, B – вектор свободных членов.
Решение такой системы можно найти как X:=A-1*B
В программе MathCAD существуют специальные функции для решения систем уравнений: функция lsolve(A,B) возвращает вектор Х.
Функции для решения уравнений.
Для уравнений F(x)=0 решение можно найти с помощью функции root(F(x),x). Эта функция реализует вычисления итерационным методом, возвращая значение переменной х, при котором функция равна нулю.
Для решения систем нелинейных уравнений используется специальный вычислительный блок
Задание начальных условий
Given
Уравнения [и ограничения]
Выражения с функциями Find или Minerr
Функция Find используется, когда решение реально существует, функция Minerr пытается найти максимальное приближение даже к несуществующему решению. При вводе системы уравнений используется оператор = (логический).
Решение системы нелинейных дифференциальных уравнений.
Общим правилом для различных методов численного решения дифференциальных уравнений (ДУ) или системы ДУ является разбиение непрерывной функции y(t) на интервалы (шаги) и определение решения в конце каждого шага, т.е. в дискретные моменты времени, путем некоторой итерационной процедуры.
Для поиска решения системы ДУ с применением функций rkfixed и Rkadapt, с помощью которых производятся вычисления по методу Рунге-Кутта, необходимо задать:
начальные условия;
дифференциальное уравнение, представляемое в виде системы ДУ первого порядка;
значения коэффициентов, входящих в уравнения;
набор точек, в которых следует найти решение.
В функцию rkfixed(y,x1,x2,n,F) входят следующие параметры:
y – вектор начальных условий с размерностью, соответствующей порядку k ДУ или числу уравнений первого порядка в системе ДУ;
x1,x2 – граничные значения интервала, на котором ищется решение;
n – число фиксированных шагов или точек, на которых ищется приближенное решение;
F – вектор, в котором записаны правые части ДУ
В результате решения ДУ с помощью этих функций получается матрица, содержащая (k+1) столбцов и (n+1) точек. В первом столбце содержатся фиксированные значения аргумента t0,t1,t2,…tn; во втором – соответствующие им значения искомой функции y(t0), y(t1), y(t2),… y(tn), в третьем – значения первых производных в тех же узлах и т.д.
Функция rkfixed ищет приближенное решение с постоянным шагом, с помощью функции Rkadapt осуществляется адаптивный контроль этого процесса: с более мелким шагом при быстром изменении функции и более крупным – при медленном изменении функции.[1]
Жесткие системы.
Например, в решении системы ДУ присутствуют слагаемые, одно из которых убывает очень быстро (е-1000х), а другое гораздо медленнее (е-2х). Для получения правдоподобного результата нужно выбирать маленький шаг, причем, на всем интервале интегрирования. Для интегрирования таких систем применяют специальные методы. Эти методы в MathCAD реализуют функции Stiffb, Stiffr. [2]
В таблице приведены некоторые функции для решения систем ДУ.
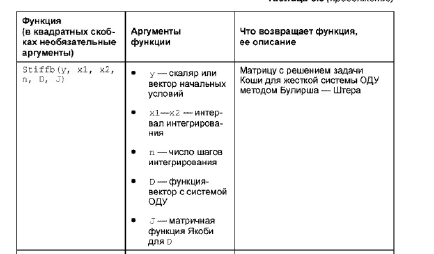
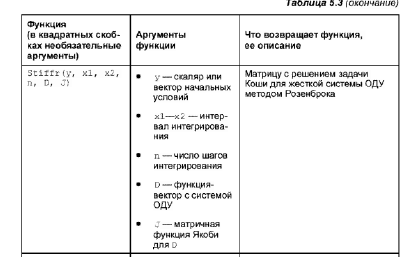
Пример программы решения системы ДУ.
Программирование в MathCAD
В MathCAD имеется специальная панель инструментов для ввода программных модулей. Программный модуль выделяется в тексте документа вертикальной жирной чертой.
Построение графиков.
График должен располагаться ниже формулы, задающей его. Удаление, копирование и перенос графиков осуществляется по той же методике, что и математических выражений. Изменение размера графика осуществляется путем протаскивания курсора, установленного на обрамляющей его рамке.
Создание графика осуществляется командой Insert-Graph или с помощью панели инструментов Graph.
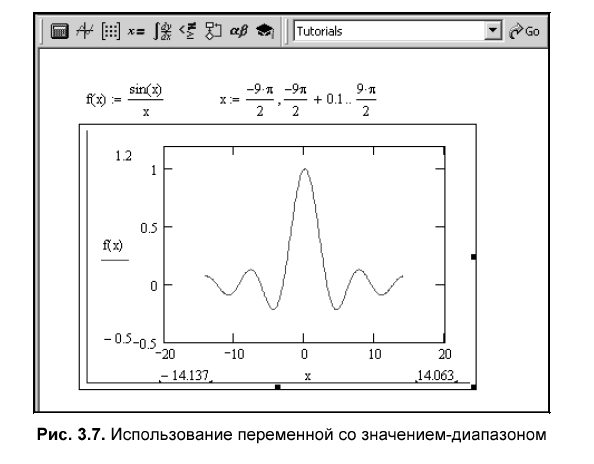
Построение графиков в декартовой системе координат.
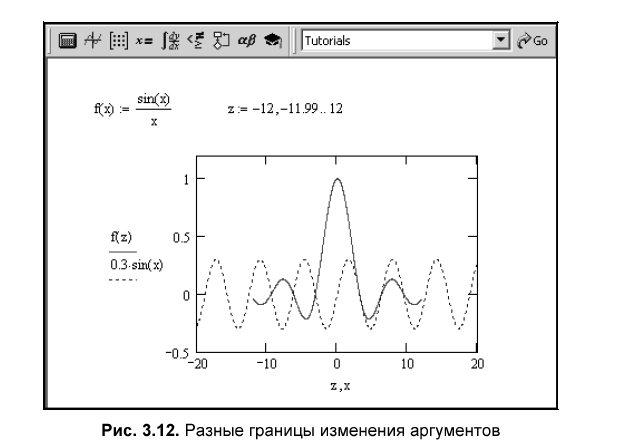
В этом случае вводится выражение для функции f(x) и пределы изменения переменной х. Выбирают шаблон двумерного графика X-Y Plot и вводят имя переменной х по оси абсцисс и имя функции по оси ординат. Если на одном рисунке необходимо отобразить графики нескольких функций, то функции имена функций перечисляются в шаблоне графика через запятую (на экране монитора эта запятая не появляется). При построении графиком можно изменить пределы изменения аргумента. Окно задания формата графика появляется, если выделить график и дважды щелкнуть левой клавишей мыши. При выделении графика и нажатии на правую клавишу мыши появляется контекстное меню, с помощью которого можно изменить отображение графика.
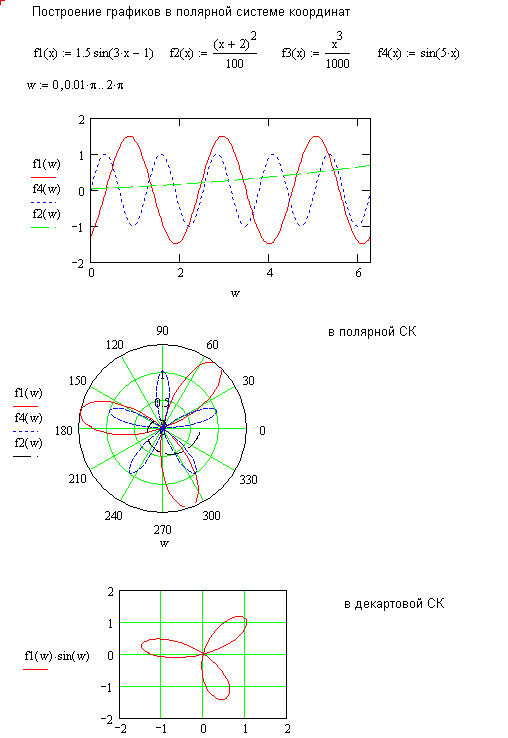
Графики в полярной системе координат.
Построение таких графиков можно осуществлять двумя способами. Можно использовать построение графика в полярной системе координат, используя шаблон Polar Plot, а можно использовать шаблон X-Y Plot. При использовании X-Y Plot по оси Х устанавливаем R(w)*cos(w), по оси Y устанавливаем R(w)*sin(w), где w – угол между горизонтальной координатной осью и радиус-вектором, R(w) – длина радиус-вектора.
Трехмерные графики.
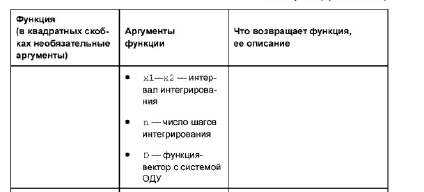
В MathCAD можно создавать график-поверхность, в том числе заданный в параметрической форме, контурный график, трехмерную гистограмму, трехмерный график рассеяния, трехмерный график векторного поля. Для изменения параметров графика используют операцию установки формата графика (угла поворота, заливки и т.п.)
Построение графиков поверхностей и линий уровня Z(X,Y) сводится к определению матрицы М значений, в которой строкам и столбцам соответствуют определенные значения X и Y, а величина элемента определяется координатой Z(X,Y). Эта матрица называется матрицей аппликат поверхности. При построении масштабы по осям X и Y не проставляются, можно вывести только порядковые номера элементов матрица аппликат.
