Приложение 2.1

Установим соотношения между зависимостями процентных ставок от периода Т по схемам простых и сложных процентов.

Имеем , . При .

Производные по Т при Т = 0

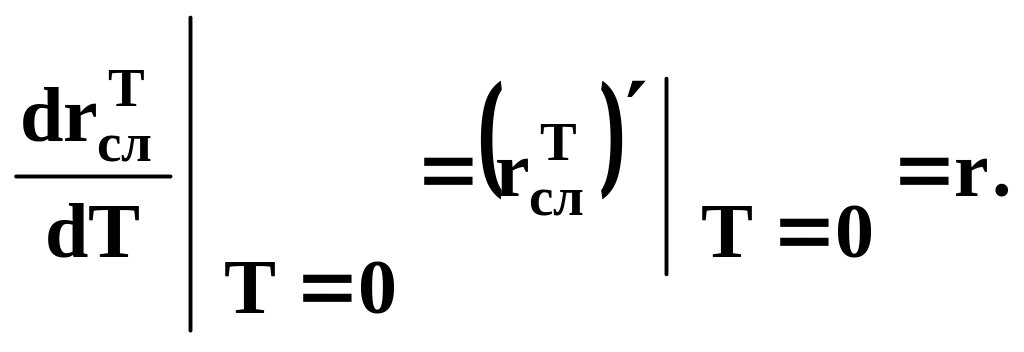
Докажем, что ln(1 + r) < r для любого r > 0 .

Рассмотрим ряд

e^r = 1 + r + r² + ... + rⁿ + ... ,

который сходится при любом значении r [А.Ф.Бермант, И.Г.Араманович. Краткий курс математического анализа для втузов. М., Наука, 1967,стр.674]. Последнее выражение можно представить

e^r = 1 + r + Q ,

где (при r > 0)

Q = r² + ... + rⁿ + ... + ...> 0 .

Из приведенных соотношений следует

e^r > 1 + r .

Логарифмируя левую и правую часть этого неравенства, получим

r > ln(1 + r),

что и требовалось доказать.

Таким образом

Поскольку при Т = 0 , то это значит, что в окрестности точки Т = 0 при положительных Т .

Функция является монотонно возрастающей.

Действительно, при t > 0

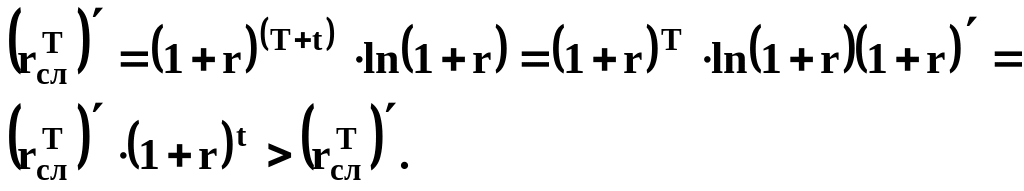
Поскольку = r и не зависит от Т , то из графического представления зависимостей и следует, что наклон касательной к графику функции , будучи при Т 0 меньше r , с ростом Т увеличивается неограниченно и монотонно , и при некотором Т станет больше r . При дальнейшем увеличении Т график пересечет график . При Т , превышающем абсциссу точки пересечения > . Из приведенных соображений следует, что точка пересечения графиков и единственная. Так как при Т = 1

то именно Т = 1 является единственной точкой пересечения графиков и . То есть

< при 0<T<1 ,

> при T>1.

Приложение 2.2

Excel XP Excel 2000

БС(r,n,C,S(0))	БЗ(r,n,C,S(0))
КПЕР(r,С,S(0))	КПЕР(r,С,S(0))
ПЛТ(r,n,S(0))	ППЛАТ(r,n,S(0))
ПС(r,n,C,S(n))	БЗ(r,n,C,S(n))
СТАВКА(n,C,S(0),S(n),,предпол.)	НОРМА(n,C,S(0),S(n),,предпол.)
ЧПС(rT,<значения>)	НПЗ(rT,<значения>)
ВСД(,<значения>,предположение)	ВНДОХ(,<значения>,предположение)
ЧИСТНЗ(r, <значения>,<даты>)	ЧИСТНЗ(r, <значения>,<даты>)
ЧИСТВНДОХ(<значения>,<даты> предположение)	ЧИСТВНДОХ(<значения>,<даты> предположение)
ЭФФЕКТ(r,m)	ЭФФЕКТ(r,m)
НОМИНАЛ(rэф,m)	НОМИНАЛ(rэф,m)

Приложение 2.3 Учёт комиссии для ссуд и кредитов.

1. Рассмотрим ссудную операцию, при которой заёмщик получает ссуду S(0) под r процентов годовых с возвратом через интервал времени T . Дополнительно будем предполагать, что сумма возврата ссуды S(T) формируется по схеме простых процентов и кредитор при выдаче ссуды удерживает комиссию . Будем считать, что заёмщик имеет возможность выбрать из нескольких кредиторов, которые отличаются процентными ставками и комиссией . С этой целью рассчитаем доходность такой операции в виде эквивалентной процентной ставки, соответствующей снижению исходной суммы на величину комиссии .

Будем рассуждать следующим образом. Кредитор рассчитывает получить наращенную сумму . Однако заёмщик получает исходную сумму (ссуду) . При такой исходной сумме кредитор получит установленную им сумму при другой (большей) процентной ставке (доходности ) : . Эту процентную ставку несложно определить путём следующих преобразований.

В условиях возможности выбора заёмщик должен рассмотреть несколько вариантов ссуды и выбрать тот из них, которому соответствует минимальная доходность (для кредитора) .

2. Пусть условия ситуации изменились лишь в том, что используется схема начисления сложных процентов. В этом случае наращенная сумма, которуюдолжен получить кредитор, равна . Тогда

(см пример расчёта в электронной таблице "комиссия", рабочий лист "комиссия_сл%).

3. Рассмотрим теперь операцию кредитования с удержанием комиссионных. Заёмщик заключает кредитный договор на кредит под процентов годовых сроком на лет с удержанием комиссии И вновь рассчитаем доходность такой операции в виде эквивалентной процентной ставки, соответствующей снижению исходной суммы кредита на величину комиссии .

Кредитор рассчитывает получить наращенную сумму .При этом ежегодное погашение кредита равно . Однако заёмщик получает исходную сумму (кредит) . При такой исходной сумме кредитор получит установленную им сумму при другой (большей) процентной ставке (доходности) и больших погасительных платежах . Исходная величина кредита и возвращённая сумма кредита определяются соотношениями .

.

Обозначим

.

Тогда

, или

, из чего следует

.

 Использование функции r = НОРМА (T;;S(0);S(T)) для расчета процентной ставки в рассматриваемой ситуации в некоторых случаях дает результат #ЧИСЛО!, то есть расчет функции не выполняется. Такое положение является следствием того, что в Excel функция НОРМА для однократных инвестиций рассчитывается как частный случай процентной ставки для потока платежей(см. раздел 2.2.1). Последняя задача в общем случае приводит к необходимости определения корня нелинейного уравнения и решается методом последовательных приближений. Если после 20 итераций погрешность определения процентной ставки превышает 0,0000001, то функция НОРМА возвращает значение ошибки #ЧИСЛО! В этом случае по рекомендации фирмы Microsoft следует подобрать начальное приближение для r = r₀ и использовать следующий формат функции r = НОРМА (T;;S(0);S(T);;r₀). Однако рациональней для однократных инвестиций в рассматриваемой ситуации отказаться от использования табличной функции и воспользоваться явным выражением для расчета процентной ставки .

 См. сноску на стр. 51

 См. cноску на стр. 51

119