2.1.4 Эффективная ставка процента

В практике финансовых расчетов используются схемы, при которых проценты на капитал начисляются несколько раз в году. При этом оговариваются годовая процентная ставка r и количество начислений в течение года m . Фактически в этом случае за базовый период принимается 1/m часть года со ставкой сложных процентов r/m .

В результате

.

Пример. Облигация номиналом 100 т.руб. выпущена на 5 лет при номинальной (годовой) ставке процента 10 %. Держатель облигации будет капитализировать проценты. Определить наращенную стоимость при начислении процентов 1 раз в год (m = 1), раз в полугодие (m = 2), раз в квартал (m = 4).

(Облигация - долговое обязательство эмитента, выпустившего ценную бумагу, уплатить владельцу облигации в оговоренный срок номинальную стоимость бумаги и через оговоренные периоды - фиксированный или плавающий процент.)

Приведем расчеты для примера.

m = 1 , S(5) = ,

m = 2 , S(5) = ,

m = 4 , S(5) = .

При количестве начислений m в течение года годовая ставка процента r называется номинальной. Чем больше количество начислений m , тем больше наращенная стоимость S(T).

Годовая ставка , обеспечивающая то же значение наращенной суммы S(T) при одноразовом в течение года начислении процентов, что и m - разовое со ставкой , называется эффективной ставкой.

По определению

= ,

и, следовательно,

= ,

то есть

= - 1 .

Электронные таблицы Excel позволяют рассчитать эффективную процентную ставку по номинальной и решить обратную задачу с помощью табличных функций . Их формат имеет вид

=ЭФФЕКТ(r;m) ,

= НОМИНАЛ( ;m) .

Расчет эффективных ставок необходим для сопоставления и выбора наиболее доходного варианта инвестиций. Так, если в условиях рассматриваемой задачи с многократным в течение года начислением процентов оказывается больше процентной ставки в операции с начислением процентов один раз в год, то первая из операций является предпочтительной для инвестора.

Эффективная ставка обладает свойством  r . Докажем это свойство. Для этого воспользуемся выражением для бинома Ньютона

(1 + x)^m = 1 + mx + +...+ =

= 1 + mx + + .. + x^m .

Используя это разложение для эффективной ставки при x = , получим

= 1 + m + + .. + =

= 1 + r + Q , где Q > 0.

Тогда = (1 + r/m)^m - 1 > 1 + r - 1 = r .

Для предыдущего примера рассчитаем эффективные ставки для m = 1;2;4 .

m = 1, = - 1 = r ,

m = 2, = - 1 = (1.05)² - 1 = 0.1025 > 0.1 = r,

m = 4, = - 1 = (1.025)⁴ - 1 = 0.1038 > 0.1 = r.

2.1.5 Модели дисконтирования

Рассмотрим процедуру дисконтирования, то есть приведения будущей суммы S(T) к моменту t = 0 .

S(0) = S(T)(1 - d_T) = S(T)V_T ,

V_T = 1 - d_T = .

Для приведения дисконта d_T и дисконт-фактора V_T к базовому периоду (году) будем использовать полученные ранее соотношения для процентных ставок.

Пусть годовая учетная ставка (дисконт) равна d , а дисконт-фактор - V . Тогда для схемы простых процентов

r_T = r T и V_T = .

Для схемы сложных процентов

1 + r_T = (1 + r)^T и V_T = .

При этом дисконтированная сумма равна

.

В таблице Excel этой формуле соответствует функция

ПЗ(r;T;;S(T))

Так как

1 - d = ,

то

V_T = (1 - d)^T = V^T ,

где V = 1 - d .

Пример. В банк предъявлен вексель на сумму 20 млн.руб., который содержит обязательство выплатить владельцу эту сумму 15.06.95. Владелец предъявил вексель досрочно 15.04.95 и банк согласился выплатить сумму (учесть вексель), но с дисконтом исходя из процентной ставки 120 % годовых.

Имеем

S(0) = V_T S(T) .

Для схемы простых процентов

V_T = = = 0.83 и

S(0) = = 16.6 млн.руб.

Для схемы сложных процентов

V_T = V^T = = 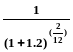= 0.877 ,

S(0) = V^T S (T) = = 17.54 млн.руб.

Рассмотрим V_T = (1 - d)^T как функцию d и разложим ее в ряд Маклорена.

[Ряд Маклорена для функции имеет вид

Имеем

V_T = (1 - d)^T =

= 1 - Td + .

При малых Td

V_T  1 - Td .

Последнее выражение используется в банковской практике и называется банковским дисконтом (банковским учетом). При значениях Td < 0.1 банковский дисконт с точностью до 1 % дает тот же результат, что и математический дисконт-фактор V_T = (1-d)^T .