Сегодня занял я дукат,

Дукату я безумно рад. Но завтра отдавать мне два -

Какие горькие слова!

2. Модели финансовой математики

Финансовая математика изучает соотношения между размерами платежей, сроками выплат и процентными ставками, возникающими в коммерческих сделках и финансово-банковских операциях.

2.1 Модели однократных инвестиций капитала

2.1.1 Основные понятия.

Простейшей финансовой операцией является предоставление в долг в некоторый начальный момент t = 0 суммы S(0) с условием, что в момент t = T будет возвращена сумма S(T).

Эффективность такой операции определяется показателями . и .

= ,

где называется процентной ставкой;

= ,

где называется дисконтом, учетной ставкой.

Введенные показатели взаимосвязаны. Действительно

1 + = ,

1 - = , и, следовательно,

1+ = , = ;

1 - = , = .

Наиболее важными являются соотношения

S(T) = S(0) (1 + ) ,

S(0) = S(T)(1 - ).

Последние выражения используются для определения наращенной суммы (стоимости) S(T) по первоначальному капиталу S(0) и процентной ставке и для определения первоначального капитала S(0) по известным наращенной стоимости S(T) и учетной ставке (дисконту) . Операция приведения наращенной суммы S(T) в момент t = T к моменту t = 0 называется дисконтированием.

Наряду с дисконтом для операции дисконтирования используется дисконт-фактор

= 1 - = = .

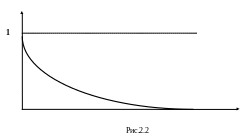
Вид графиков зависимостей дисконта и дисконт-фактора от процентной ставки представлены на рис.2.1 и 2.2.

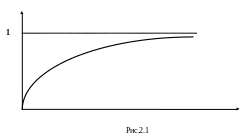
Пример. Фирма взяла кредит 300 млн.руб. в банке сроком на 1год под 12 % годовых. Какая сумма должна быть возвращена через год ?

Здесь = 12 % ,

S(1) = S(0) (1 + ) = 300(1 + 0.12) = 336 млн.руб.

= = = 10,7%

= 1 - = 0.893 = = .

В условиях финансовых операций как правило оговариваются процентная и учетная ставки за базовый период, равный году. Соответствующие показатели за фактический период T ( и ) рассчитываются по формулам, зависящим от дополнительных условий сделки. Будем называть процентную и учетную ставки за год годовыми и обозначать их через r и d . Рассмотрим приведение годовых процентных и учетных ставок к периоду T для различных схем, используемых в финансовой практике.

2.1.2 Схема простых процентов

Схема простых процентов предполагает начисление процентов к базовому капиталу S(0). При этом, если T больше года и начисление процентов осуществляется после каждого года, то наращенная стоимость будет равна

S(T) = S(0) + rS(0) + rS(0) +...+ rS(0) =

T раз

= S(0) (1 + rT) = S(0) (1 + ) .

(Для простоты первоначально полагаем, что T равно целому числу лет).

Из приведенного соотношения имеем

= и

Обычно схема простых процентов используется в практике банковских расчетов для периодов T < 1 года.

Пример. Пусть выдан кредит 100 млн.руб. с 25.03.97 по 25.06.97 под 60 % годовых. Сумма погашения кредита рассчитывается по формуле

S(0) = S(0)(1 + rT ) ,

что при

= 60%, T = = .

S(T) = 100(1 + 0.6 ) = 115 млн.руб.