Статично невизначені задачі на розтягання (стискання)

Задача №1

В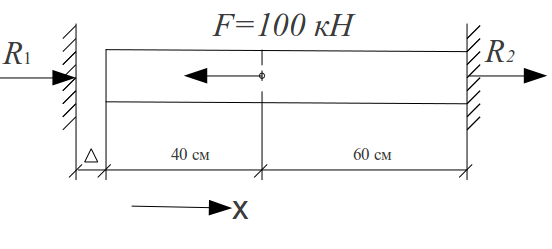 изначити напруження в лівій частині стального стержня, якщо зазор між лівою частиною та стержнем ∆=0,2 мм, площа перерізу стержня А=5 см², модуль пружності матеріалу Е=2∙10⁵МПа.

Рис. 71

Рішення:

Під дією зовнішньої сили F стержень збільшує свою довжину на величину зазору - ∆. Далі його збільшення буде припинено за рахунок нерухомої лівої стінки, де виникне додаткова опорна реакція R₁. Тому в задачі з’являється додаткове невідоме зусилля, яке не можна знайти тільки за допомогою рівняння рівноваги:

(1)

Складаємо додаткове рівняння деформацій:

(2)

За допомогою закону Гука перетворюємо рівняння деформацій в рівняння невідомих зусиль R₁ і R₂:

(3)

Визначимо внутрішні сили N₁ та N₂ за допомогою метода перерізів:

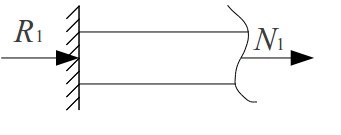
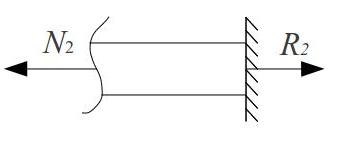
Тоді:

Підставимо отримані вирази ∆l_i в рівняння (2):

Рішимо систему рівнянь:

Напруження в лівій частині стержня буде дорівнювати:

З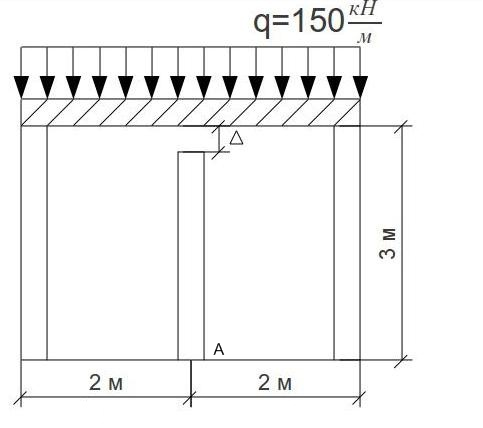 адача №2

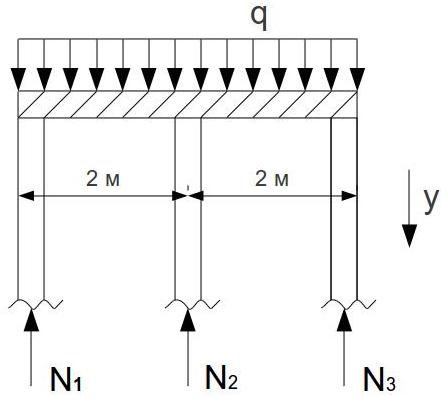
Абсолютно жорстка балка спирається на три бетонні колони (Е_б=15∙10⁵МПа) однакового поперечного перерізу А=500см². Між балкою та середньою колоною до навантаження був зазор ∆=0,4мм. Знайти напруження в усіх колонах.

Рис. 71

Рішення

Під дією зовнішнього навантаження колони стискуються на деяку величину, яка буде більше ніж зазор ∆, який був до прикладання розподіленого навантаження між жорсткою балкою та середньою колоною. Тому у всіх колонах виникнуть внутрішні сили (дивись малюнок).

Для відсіченої частини конструкції залишимо рівняння рівноваги:

якщо , то

(1)

Рис .72

Складаємо додаткове рівняння деформацій. Зміна довжини кожної колони показано на мал.3:

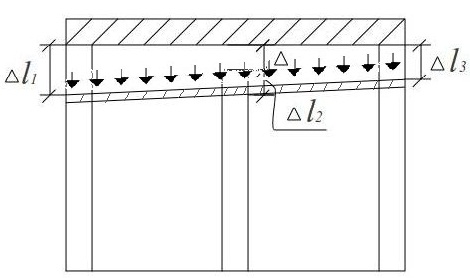
(2)

За допомогою закону Гука перетворимо рівняння деформацій в рівняння відносно невідомих зусиль N_i.

Рис .73

Підставимо записані вирази в рівняння (2):

Рішимо систему рівнянь:

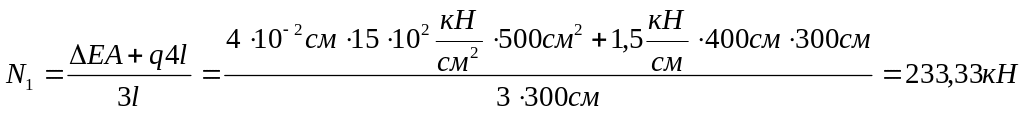
Задача №3

В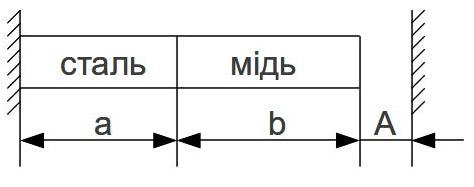 изначити напруження в стержні при підвищенні його температури на ∆t⁰=50⁰, якщо a=0,5м, b=0,6м, ∆=0,5мм.

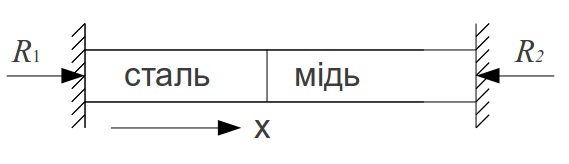
Рис .74

Коефіцієнт лінійного розширення для сталі α_ст=1,25∙10^-5 1/град, для міді α_м=1,65∙10^-5 1/град; Модуль пружності сталі: Е_ст=2∙10⁵МПа, для міді Е_м=10⁵МПа.

Розв’язок

Під дією температури стержень спробує збільшити свою довжину, тому з двох сторін виникнуть опорні реакції R₁ та R₂.

1. В изначимо ступінь статичної невизначеності, як різницю між кількістю невідомих зусиль (R₁ та R₂)

Рис .75

2. та чисто рівнянь рівноваги, які не перетворюються в тождествінний нуль.

3. Складемо можливі рівняння рівноваги:

4. Складемо додаткове рівняння деформацій:

(1)

Тобто стержень під дією температури зможе збільшити свою початкову довжину тільки не величину зазору ∆.

Рис .76

5. За допомогою закону Гука перетворимо рівняння деформацій в рівняння відносно невідомих зусиль R₁ та R₂.

Внутрішні зусилля визначимо за допомогою методу перерізів:

Підставимо отримані вирази в рівняння (1):

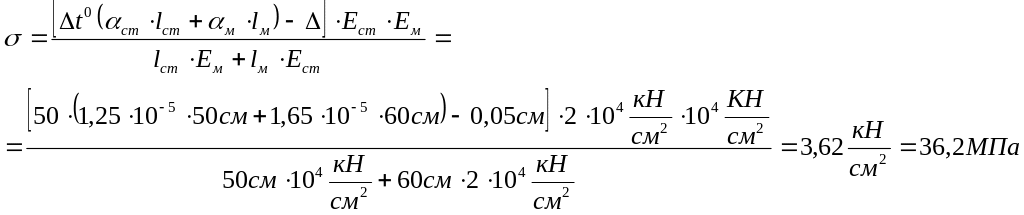
Відомо, що напруження при розтяганні (стисканні) визначається за формулою:

якщо то

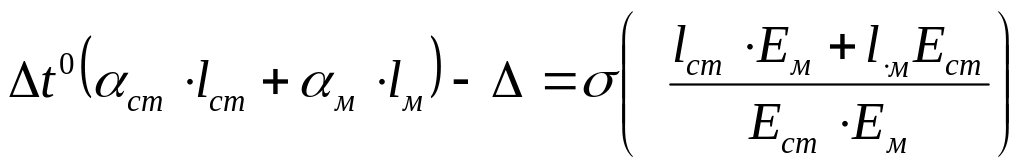
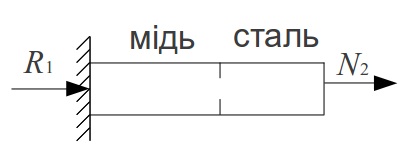
Задача №4

В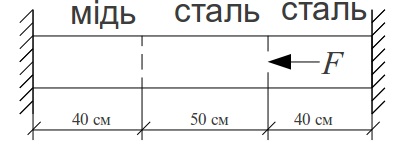 изначити напруження в стержні ліворуч від точки, в якій прикладена сила, якщо F=400кН, площа поперечного перерізу А=20 см², модуль пружності сталі Е_ст=2∙10⁵МПа, для міді Е_м=10⁵МПа.

Рис .77

Рішення:

Під дією зовнішньої сили F стержень намагається збільшити свою довжину, але за рахунок опорних реакцій в жорстких опорах зліва та справа його подовження буде дорівнювати нулю.

1. Визначимо ступінь статичної невизначеності:

Рис .78

Кількість невідомих опорних реакцій дорівнює 2.

Кількість рівнянь рівноваги, які не перетворюються у тотожний нуль – 1.

2. Складемо рівняння рівноваги:

(1)

3. Складемо додаткове рівняння деформацій:

(2)

4. За допомогою закону Гука перетворимо рівняння деформацій в рівняння відносно невідомих зусиль R₁ та R₂.

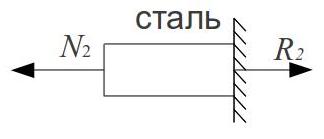
Внутрішні зусилля N₁,N₂ та N₃, визначимо за допомогою методу перерізів:

Підставимо знайдені внутрішні сили в вираз ∆l_i.

5. Вирішимо систему рівнянь, яка складається з рівняння (1) та перетвореного рівняння (2).

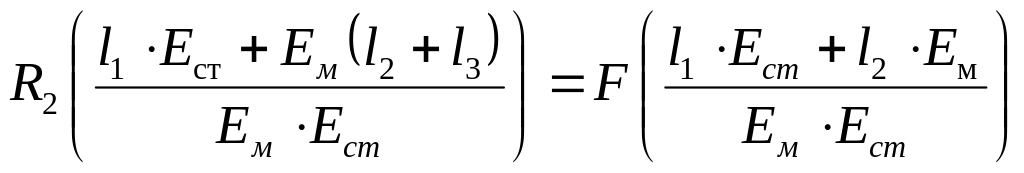
т.к. , то