Жорсткість при розтяганні без урахування власної ваги

1. Визначити повне подовження стержня, якщо F1 = 70 кH, F2 = 100 кH, F3 = 60 кH, Е = 2•10⁵ МПа, [σ] = 160 МПа.

Рис. 29

2. Визначити зміну довжини ділянки стержня довжиною 1м, якщо F1 = 70 кH, F2 = 100 кH, F3 = 60 кH, Е = 2•10⁵ МПа, [σ] = 160 МПа (рис. 29).

3. Визначити зміну довжини ділянки стержня довжиною 2 м, якщо F1 = 70 кH, F2 = 100 кH, F3 = 60 кH, Е = 2•10⁵ МПа, [σ] = 160 МПа (рис. 29).

4. Визначити зміну довжини ділянки стержня довжиною 1.5 м, якщо F1 = 70 кH, F2 = 100 кH, F3 = 60 кH, Е = 2•10⁵ МПа, [σ] = 160 МПа (рис. 29).

5. Визначити повну зміну довжини, якщо [σ] = 160 МПа, F₁ = 5 кH, F₂ = 12 кH, ℓ₁ = 40 см, ℓ₂ = 30 см, Е = 2·10⁵ МПа.

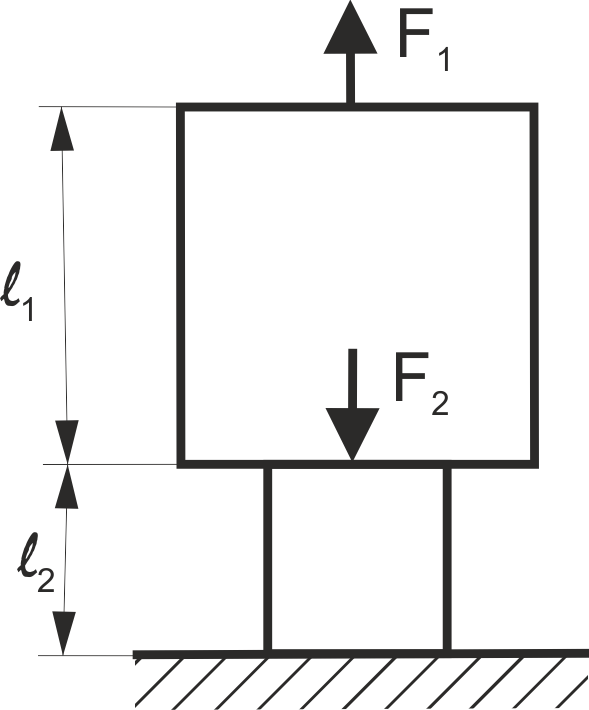
Рис. 30

6. Визначити зміну довжини верхньою частини стержня, якщо [σ] = 160 МПа, F₁ = 5 кH, F₂ = 12 кH, ℓ₁ = 40 см, ℓ₂ = 30 см, Е = 2·10⁵ МПа (рис. 30).

7. Визначити зміну довжини нижньою частини стержня, якщо [σ] = 160 МПа, F₁ = 5 кH, F₂ = 12 кH, ℓ₁ = 40 см, ℓ₂ = 30 см, Е = 2·10⁵ МПа (рис. 30).

8. Визначити зміну довжини верхньої частини стержня, якщо:F₁ = 5 кH, F₂ = 4 кH, F₃ = 2 кH, А = 10 см², Е = 2·10⁵ МПа (рис. 31).

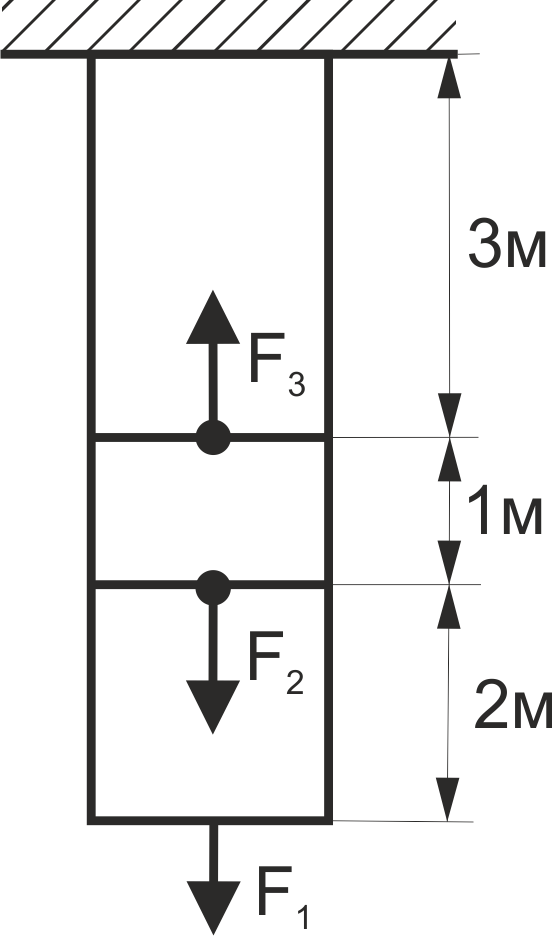
Рис. 31

9. Визначити зміну довжини середньої частини стержня, якщо:F₁ = 5 кH, F₂ = 4 кH, F₃ = 2 кH, А = 10 см², Е = 2·10⁵ МПа (рис. 31).

10. Визначити зміну довжини нижньої частини стержня, якщо:F₁ = 5 кH, F₂ = 4 кH, F₃ = 2 кH, А = 10 см², Е = 2·10⁵ МПа (рис. 31).

11. Визначити повне подовження стального стержня, навантаженого як показано, якщо площа його поперечного перерізу дорівнює 4 см², F1 = 20 кH, F2 = 10 кH, F3 = 30 кH.

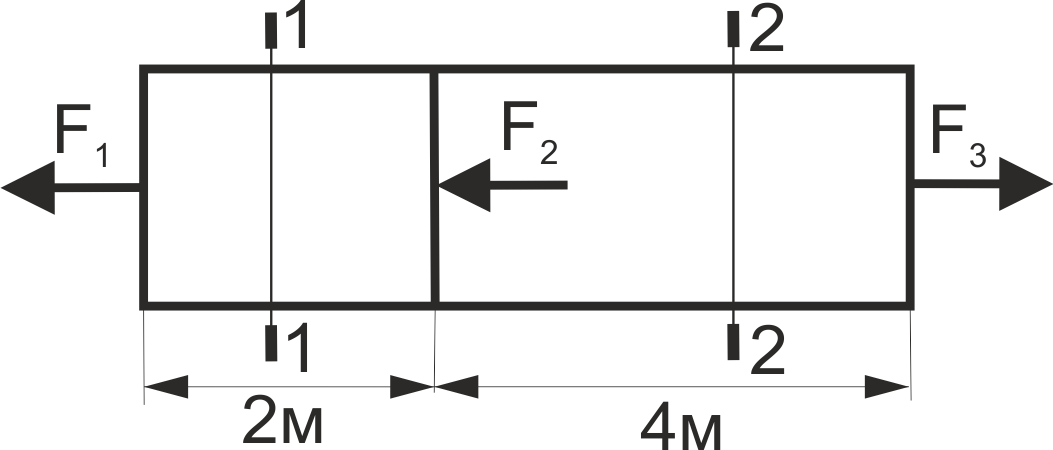
Рис. 32

12. Визначити подовження лівої частини стального стержня, навантаженого як показано, якщо площа його поперечного перерізу дорівнює 4 см², F1 = 20 кH, F2 = 10 кH, F3 = 30 кH (рис. 32).

13. Визначити подовження правої частини стального стержня, навантаженого як показано, якщо площа його поперечного перерізу дорівнює 4 см², F1 = 20 кH, F2 = 10 кH, F3 = 30 кH (рис. 32).

14. Визначити зміну довжини 2-ої ділянки стержня, якщо його довжина а=1 м; площа поперечного перерізу А=5см²; модуль пружності 1-ого рода Е = 2•10⁵ МПа

Рис. 33

15. Визначити зміну довжини 1-ої ділянки стержня, якщо його довжина а=1 м; площа поперечного перерізу А=5см²; модуль пружності 1-ого рода Е = 2•10⁵ МПа (рис. 33).

16. Визначити зміну довжини 3-ої ділянки стержня, якщо його довжина а=1 м; площа поперечного перерізу А=5см²; модуль пружності 1-ого рода Е = 2•10⁵ МПа (рис. 33).

Стержневі системи

1. Підібрати діаметр круглого перерізу сталевої тяги АВ, якщо F=100кH, а допустиме напруження для матеріалу тяг [σ]=100 МПа, Е_СТ=10⁵МПа (рис. 34).

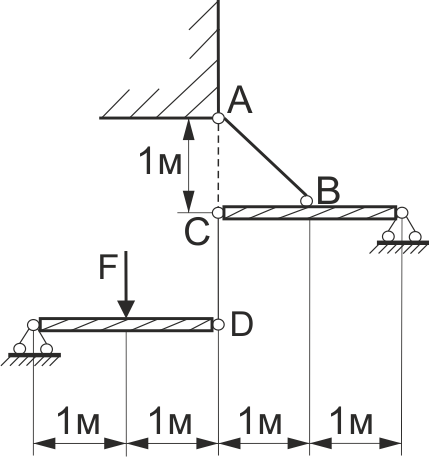
Рис. 34

2. Підібрати діаметр круглого перерізу сталевої тяги СD, якщо F=100кH, а допустиме напруження для матеріалу тяг [σ]=100 МПа, Е_СТ=10⁵МПа (рис. 34).

3. Кронштейн навантажено силою F = 60 кН. Стержень АС – сталевий, [σ]_СТ = 160 МПа, стержень ВС – дерев`яний, [σ]_Д = 4 МПа. Підібрати круглий перетин сталевого стержня.

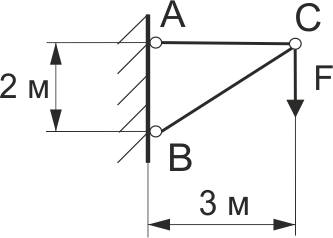
Рис. 35

4. Кронштейн навантажено силою F = 60 кН. Стержень АС – сталевий, [σ]_СТ = 160 МПа, стержень ВС – дерев`яний, [σ]<sub>Д</sub> = 4 МПа. Підібрати квадратний перетин дерев`яного (рис. 35).

5. Вказати вірне значення діаметру стержня 1, якщо F₁ = 20 кH, [σ]₁ = 120 МПа, F₂ = 30 кН, [σ]₂ = 160 МПа.

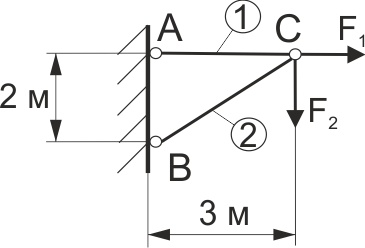
Рис. 36

6. Вказати вірне значення діаметру стержня 2, якщо F₁ = 20 кH, [σ]₁ = 120 МПа, F₂ = 30 кН, [σ]₂ = 160 МПа (рис. 36).

7. Знайти площу поперечного перерізу стержня AB конструкції, яка вказана на рисунку, якщо [σ = 160 МПа, F = 50 кH.

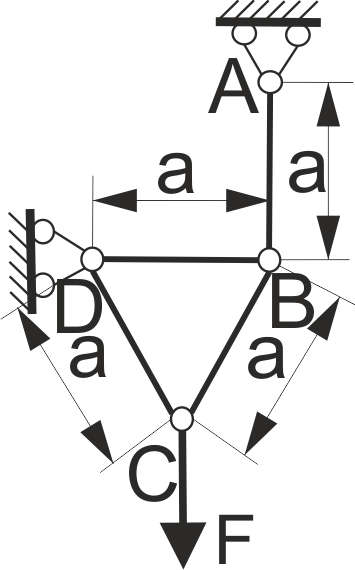
Рис. 37

8. Знайти площу поперечного перерізу стержня DB конструкції, яка вказана на рисунку, якщо [σ] = 160 МПа, F = 50 кH (рис. 37).

9. Знайти площу поперечного перерізу стержня BC конструкції, яка вказана на рисунку, якщо [σ] = 160 МПа, F = 50 кH (рис. 37).

10. Сила F прикладена до двох стержнів, як зображено на рисунку. α = 20˚, β = 35˚. Стержень АС − стальний, [σ] = 200 МПа, d = 5 см; стержень ВС − мідний, d = 6 см, [σ] = 100 МПа. Яке значення сили F можна прикласти до точки С?

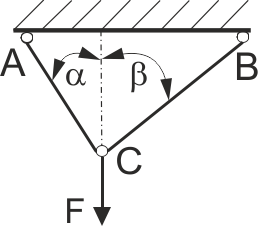
Рис. 38

11. Жорсткий стержень АВ навантажено силою F й підтримується стальною тягою DC круглого поперечного перерізу d = 2 см. Визначити найбільше допустиме навантаження F. Допустиме напруження матеріалу тяги DC дорівнює 160 МПа, Е_СТ = 2·10⁵ МПа.

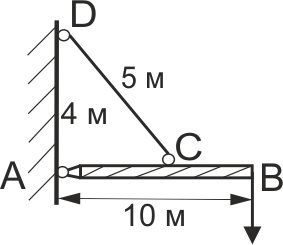
Рис. 39

12. Визначити площу поперечного перерізу А лівого стержня , якщо

F = 100 кН, l = 2 м, Е = 2·10⁵ МПа,  σ  = 160 МПа, α = 60˚.

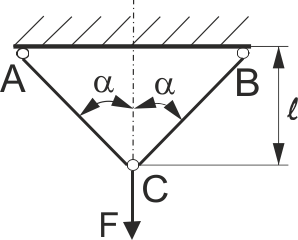
Рис. 40

13. Визначити площу поперечного перерізу А правого стержня, якщо

F = 100 кН, l = 2 м, Е = 2·10⁵ МПа,  σ  = 160 МПа, α = 60˚(рис. 40).