2.2. Обратные матрицы. Задачи

1. Доказать следствие 2.1.

2. Доказать следствие 2.2.

3. Доказать следствия 2.3 -2.5.

4. Как изменится обратная матрица , если в данной матрице А: а) переставить -ю и -ю строки; б) -ю строку умножить на отличное от нуля число ; в) к -й строке прибавить -ю строку, умноженную на число ? Ответить на этот же вопрос в случае аналогичных преобразований столбцов матрицы А.

5. Пусть А и В – невырожденные матрицы одного порядка. Тогда матрица также невырожденная, причем .

6. Пусть А – квадратная невырожденная матрица. Тогда

.

7. Решить систему линейных уравнений матричным методом (с помощью обратной матрицы):

а) ,

б) ,

в) ,

г) ,

д) ,

е) ,

ж) ,

з) .

2.3. Ответы, указания, решения.

4. Ответы. а) в матрице поменяются местами -й и -й столбцы; б) -й столбец в матрице умножится на ; в) из -го столбца вычтется -й столбец, умноженный на .

5. Решение. , поэтому матрица - обратная для АВ. Это означает также, что АВ – невырожденная (в силу следствия 3.2).

6. Решение. Так как (см. теорему 1.12), то обратная для .

7. З). Решение. Перепишем систему в матрично-векторном виде: где

Согласно следствию 2.5, если матрица А невырожденная, то решением этой системы будет вектор-столбец . Поэтому воспользуемся практическим правилом проверки невырожденности матрицы и построения обратной для нее матрицы (в случае утвердительного ответа), описанным ранее:

,

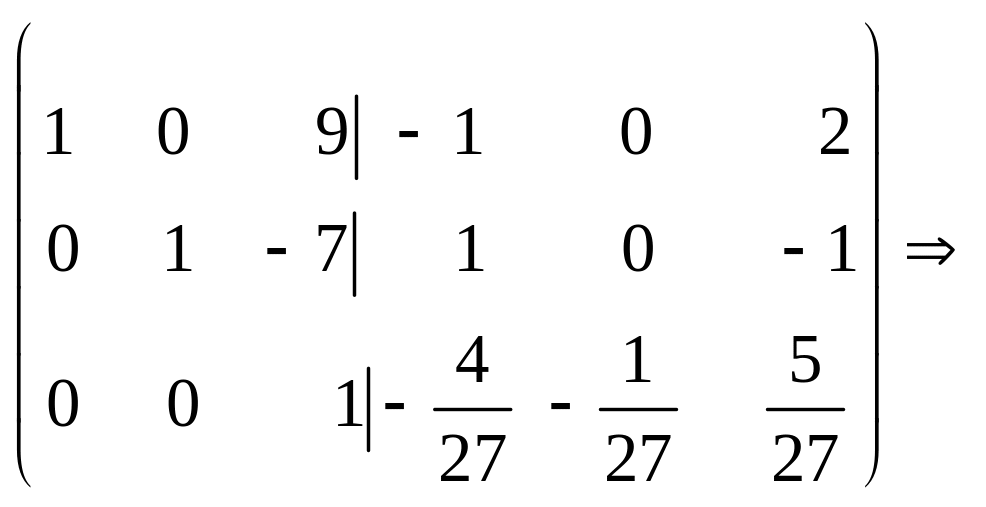
откуда

.

Тогда искомое решение определяется равенством:

.

2.4. Определители. Математическая часть

Условимся в дальнейшем через обозначать матрицу, полученную из матрицы удалением -й строки и -го столбца. Считаем также, что на позиции в находится элемент .

Каждой квадратной матрице по определенному правилу ставится в соответствие некоторое число, называемое определителем матрицы и обозначаемое через . Ниже дается интуитивное определение этого понятия.

Определение. Если квадратная матрица имеет порядок 1, то ее определитель равен . Если порядок квадратной матрицы А больше 1, то алгебраическим дополнением элемента в матрице А называется число , которое будет обозначаться (здесь - определитель матрицы . Определителем матрицы называется сумма произведений элементов первой строки на соответствующие им алгебраические дополнений:

Пример. Вычислим определитель матрицы второго порядка:

.

В приведенном выше вычислении определителя первая строка играет особую роль. Однако следующая теорема, приводимая без доказательства, показывает, что в этой роли может выступать любая строка или любой столбец.

Теорема 2.2. Определитель квадратной матрицы А, порядок которой больше 1, равен сумме произведений элементов любой строки (столбца) на соответствующие им алгебраические дополнения:

( ).

Эти равенства называются разложением определителя по -й строке ( -му столбцу).

Свойства определителей:

Свойство 2.1. Если квадратная матрица содержит нулевую строку (нулевой столбец), то ее определитель равен 0.

Свойство 2.2. При перестановке любых двух строк (столбцов) определитель меняется на противоположное число.

Доказательство. Предположим, что в А переставляются две соседние строки: -я и . Вновь полученную матрицу обозначим В. Очевидно, что для каждого .Но . Поэтому Разложим теперб определитель матрицы В по - й строке:

.

Теперь предположим, что нужно переставить -ю и -ю строки в матрице А. Эту перестановку можно осуществить посредством перестановок соседних строк:

… , , …,

(в скобках указаны переставляемые строки). Поэтому для полученной после этих перестановок матрицы В верно следующее:

,

что завершает доказательство. Доказательство утверждения для столбцов проводится аналогично.

Свойство 2.3. Если квадратная матрица имеет хотя бы две одинаковые строки (два одинаковых столбца), то ее определитель равен нулю.

Доказательство. Если в матрице А переставить две одинаковые строки (два одинаковых столбца), то новая матрица будет совпадать с А и поэтому с учетом свойства 2.2 , что возможно только при

Свойство 2.4. Сумма произведений элементов произвольной -й строки соответственно на алгебраические дополнения к этим элементам произвольной другой -й строки из тех же столбцов равна нулю:

.

Аналогичное утверждение верно и для столбцов.

Доказательство. Заменим в А -ю строку -й строкой. В полученной матрице В -я и -я строки уже одинаковы, т.е. по свойству 2.3. Разложим по -й строке:

что и требовалось доказать.

Свойство 2.5. Пусть - матрица, полученная при умножении строки (столбца) квадратной матрицы А на число . Тогда .

Для доказательства свойства достаточно разложить определитель полученной матрицы по строке, которая была умножена на .

Теорема 2.2. Определитель матрицы остается неизменным при элементарных преобразованиях строк (столбцов) типа 2.

Доказательство. Предположим, что матрица В получена из матрицы А прибавлением к -й строке -й строки, умноженной на . Разложим определитель матрицы В по -й строке. Тогда с учетом имеем:

так как по свойству 2.4. Теорема доказана.

Теорема 2.2. подсказывает практический способ вычисления определителя, который состоит в следующем. Если -я строка (столбец) в матрице А состоит из одного ненулевого элемента , то по теореме 2.1 Тем самым вычисление определителя порядка сводится к вычислению определителя порядка . Хотя в матрице А может не оказаться строк (столбцов) с нужным числом нулей, тем не менее с помощью элементарных преобразований типа 2 А можно преобразовать к нужному виду. При этом величина определителя останется неизменной в силу теоремы 2.2.

Следствие 2.6. Квадратная матрица А невырождена, если и только если ее определитель отличен от нуля.

Доказательство. Согласно следствию 1.6 , с помощью элементарных преобразований строк матрицу А можно привести либо к единичной матрице в случае невырожденности А, либо к матрице, содержащей нулевую строку, в случае вырожденности А. В первом случае в силу теоремы 2.2 и свойства 2.5, во втором случае

в силу свойства 2.1. Следствие доказано.

Определение. Матрица

называется присоединенной для квадратной матрицы А.

Следствие 2.7. Если , тио матрица является обратной для А.

Доказательство. Элемент матрицы на позиции равен . Но при эта сумма равна (теорема 2.1), а при эта сумма равна нудю (свойство 2.4). Поэтому

=

откуда , что доказывает следствие.

Пример.

Если то ,

.