1.5. Матрицы. Компьютерная часть

Индексы матриц и векторов в Mathcad могут принимать целые неотрицательные значения. Начало индексации (нумерации) строк и столбцов матриц задается системной переменной . Например, означает, что нумерация строк и столбцов начинается с нуля. По умолчанию значение переменной равно нулю.

Ввод элементов матрицы аналогичен вводу координат векторов. Пусть, к примеру, надо ввести матрицу В нужном месте рабочего листа введите имя матрицы и знак присваивания . Затем выведите диалоговое окно Вставить матрицу (Insert Matrix). В поле Строк (Rows) этого окна надо задать число строк 3, а в поле Колонок (Columns) – число столбцов 2. После щелчка кнопкой OK справа от знака присваивания появится шаблон матрицы с метками для ввода ее элементов:

Чтобы извлечь элемент матрицы, находящийся на позиции , необходимо набрать имя матрицы с индексами (индексы – через запятую) в случае равенства единице или с индексами в случае равенства нулю. Рассмотрим, например, элемент 8ю2 матрицы , который находится на позиции (3,2). Предположим, что равно нулю. Для извлечения элемента 8.2 наберите имя матрицы , затем комбинацией клавиш перейдите в режим ввода индексов: . Введите на месте метки индексы 2,1. Клавишей введите знак равенства, справа от которого появится искомый элемент: .

Некоторые операции над матрицами производятся с помощью подпанели Матрица (Matrix). Щелчок на кнопке сразу же после ввода имени матрицы приводит к транспонированию этой матрицы. Щелчок по кнопке сразу же после ввода имени матрицы приводит к появлению шаблона с меткой для ввода номера столбца матрицы: . На месте метки надо ввести номер того столбца, который требуется извлечь. Например, (в случае равенства нулю).

Стандартные функции и определяют соответственно число строк и столбцов матрицы М. Например, и .

1.6. Матрицы. Задачи

1. Пусть А и В – квадратные матрицы одного и того же порядка. Всегда ли выполняется равенство АВ=ВА?

2. Матрицы А и В называются перестановочными, если АВ=ВА. Доказать, что квадратная матрица А перестановочна со всеми квадратными матрицами того же порядка, если и только если А=кЕ, где к – некоторое число.

3. Найти матрицы и , где

а) , , ;

б) , , ;

в) , , ;

г) , , ;

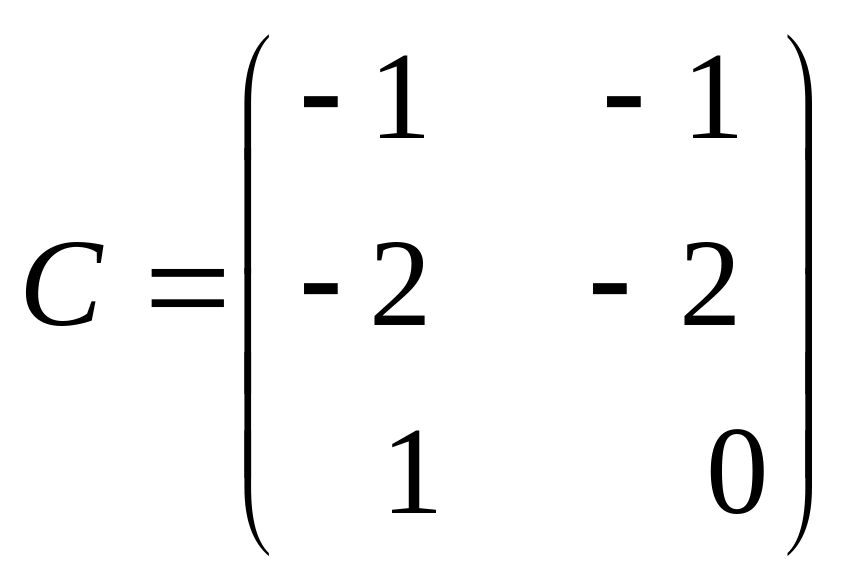4. Предприятие выпускает видов продукции с использованием видов сырья. Нормы расхода сырья даны в матрице А, в которой на позиции находится число, равное количеству расходуемого сырья (кг) -го вида на производство единицы продукции -го вида. Плановый объем выпуска продукции дан в векторе-строке , в которой -й элемент равен количеству единиц продукции -го вида. Вектор-строка задает себестоимость единицы сырья каждого вида, а вектор-строка задает транспортные расходы на единицу сырья каждого вида ( -е элементы этих векторов соответствуют -му виду сырья). Пользуясь только умножением матриц, найти: количество сырья каждого вида для выполнения планового выпуска продукции; производственные и транспортные затраты на сырье, расходуемое на производство единицы продукции каждого вида; затраты на все сырье, необходимое для выполнения плана.

а) ,

б) ,

5. Данные о дневной производительности 6 предприятий, выпускающих пять видов продукции, приведены в матрице

,

в которой на позиции находится дневная производительность (изделий в день) -го предприятия по -му виду продукции. Нормы расхода сырья трех видов даны в матрице

,

в которой на позиции находится число, равное количеству (кг) расходуемого сырья -го вида на производство единицы продукции -го вида. Даны также вектор-строка , содержащая количество рабочих дней в году по каждому предприятию, и вектор-строка цен единицы сырья каждого вида:

,

Требуется найти: годовую производительность каждого предприятия по каждому виду продукции; годовую потребность каждого предприятия по каждому виду сырья; годовую сумму кредитования каждого предприятия для закупки сырья, необходимого для выпуска всей продукции.

Ответ задаче 3 г).

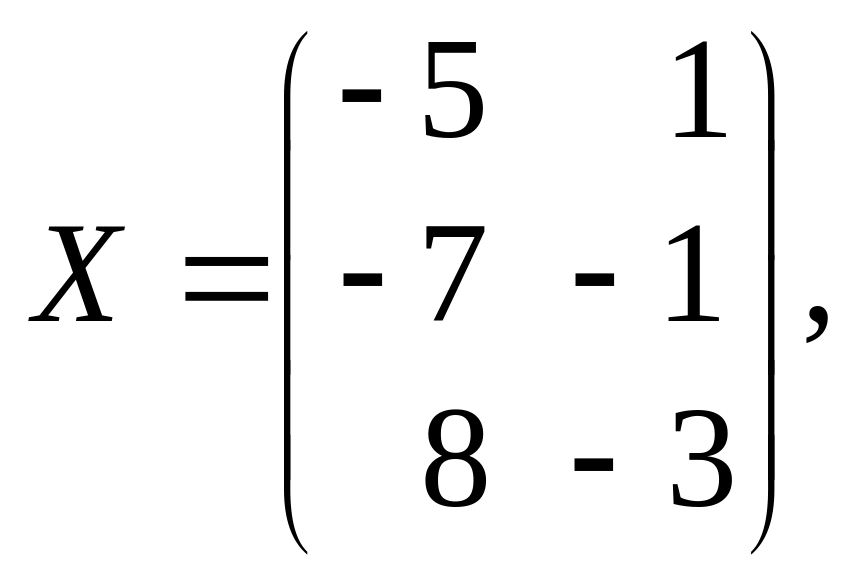
Ответ к задаче 4 б).

4222678.2.

Указание к задаче 5. Ввести исходные данные: матриц А,В, вектор строк . Определить годовую производительность каждого предприятия по каждому виду продукции:

, ,

(в матрице на позиции будет число, равное годовой производительности -го предприятия по -му виду продукции).

Определить годовую потребность каждого предприятия по каждому виду сырья: (в матрице элемент на позиции будет равен годовой потребности -го предприятия в -м виде сырья).

Определить годовую сумму кредитования каждого предприятия для закупки сырья, необходимого для выпуска всей продукции (в векторе-строке -й элемент равен сумме, которая необходима для закупки сырья всех видов -м предприятием).