2. Ядерные уровни энергии

Так же, как и в атоме, полная внутренняя энергия ядра E_вн имеет определенные дискретные уровни. Под E_вн понимается сумма кинетической энергии и потенциальной энергии взаимодействия нуклонов. Уровни энергии ядра лежат достаточно далеко друг от друга вблизи основного состояния и все теснее сближаются с ростом энергии. Схема расположения уровней энергии для ядер различной массы показана на рис. 2.2.1.

Уровни энергии ядер Средние и тяжелые ядра А=(100¸250) Легкие ядра

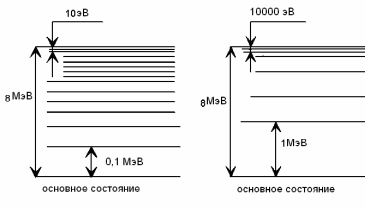
Рис. 2.2.1.

Особый интерес представляет расположение уровней энергии около энергии возбуждения E_в = 8 МэВ, так как таков порядок величины энергии возбуждения, полученный при поглощении нейтрона. Так как возбужденное промежуточное ядро является неустойчивым, то каждое его возбужденное состояние характеризуется средним временем жизни t и шириной уровня G. Ширина уровня G характеризует неопределенность в величине энергии данного состояния. Эти величины связаны соотношением Гейзенберга

Полная ширина Г для данного возбужденного состояния ядра определяется как сумма парциальных размеров ширины этого состояния для различных видов распадов, которые могут произойти с возбужденным ядром

G = SG_i

Ширина уровня G пропорциональна вероятности распада составного ядра в единицу времени.

3. 0Резонансное поглощение

Пусть на слой вещества падает стационарный поток нейтронов. Будем считать, что энергию падающих нейтронов мы можем плавно менять. Тогда можно заметить, что для определенных значений кинетической энергии нейтрона наблюдается резкое увеличение вероятности захвата частиц ядрами вещества с образованием составного ядра. Это явление получило название резонансного поглощения. Резонансное поглощение происходит в том случае, когда энергия падающей частицы такова, что образуемое промежуточное ядро близко к одному из его квантовых состояний. Схема расположения уровней энергии ядра мишени и составного ядра приведена на рис. 2.3.1.

Уровни энергии ядра - мишени и составного ядра

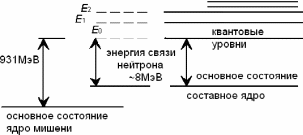
Рис. 2.3.1.

Энергия E₀ соответствует возбужденному состоянию составного ядра при захвате ядром - мишенью нейтронов с нулевой кинетической энергией (931 МэВ – энергия покоя нейтрона).

Нейтрон, попадая в поле ядерных сил, разгоняется и при непосредственном столкновении отдает не возбуждению E = 8 МэВ. Поэтому, зная энергию E₀, можем найти уровень основного состояния составного ядра, а затем уже можем начертить расположение квантовых уровней составного ядра.

В зависимости от кинетической энергии падающего нейтрона вновь образуемое составное ядро имеет различную энергию возбуждения. Согласно схеме на рис. 2.3.1. при нулевой кинетической энергии нейтрона составное ядро не будет находиться в своем квантовом состоянии. Если же нейтрон имеет кинетическую энергию, равную E_n = E₁ - E₀ = E^*_к, то в этом случае образуемое составное ядро будет иметь энергию, соответствующую квантовому уровню, поэтому вероятность захвата нейтрона с энергией E_к = E₁ - E₀ будет значительной. Существует также еще ряд энергий нейтрона, при которых будет наблюдаться резонансный захват (например, E_к = E₂ - E₀).

Согласно квантовой механике каждый из возбужденных уровней имеет определенную ширину, так как имеет конечное среднее время жизни. В соответствии с этим существует некоторый интервал энергий нейтрона, при которых будет происходить резонансное поглощение. Если ширина квантового уровня становится сравнимой с расстоянием между уровнями, то понятие резонансного поглощения становится неприемлемо. При энергии возбуждения E_в » 8 МэВ расстояние между уровнями на тяжелых ядрах составляет (1¸10) эВ. В этом случае нейтроны, обладающие кинетической энергией в пределах E » (1¸100) эВ, будут резонансными. Если же мы будем иметь дело с легкими ядрами, то расстояние между уровнями при E_возб » 8 МэВ имеет значение порядка 10⁴ эВ, т.е. резонансное поглощение будет наблюдаться при энергии нейтрона Е_n » 10⁴ эВ, но при этом само сечение поглощения резко уменьшается, и ярко выраженных резонансов не наблюдается.

При кинетической энергии нейтрона ~ 1 МэВ образующееся составное ядро будет иметь энергию возбуждения примерно Е_в » 9 МэВ. Но при таких энергиях расстояния между уровнями становятся одного порядка с шириной уровня, поэтому резонансное поглощение в этом случае отсутствует.

На изолированном резонансе зависимость сечения захвата нейтрона от энергии описывается формулой Брейта - Вигнера, полученной методами квантовой механики:

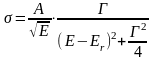
где А - некоторая постоянная, Е_r - резонансная энергия нейтрона, Е – энергия нейтрона, Г – ширина уровня. Примерный график зависимости s(Е) приведен на рис. 2.3.2.

Зависимость сечения взаимодействия нейтронов с ядрами от энергии в области резонанса

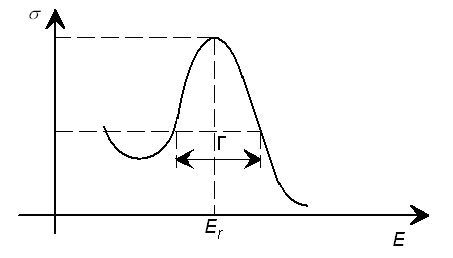
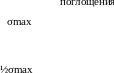
Рис. 2.3.2.

Рассмотрим несколько важных частных случаев:

1) при Е = Е_r сечение захвата максимально

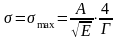
2) если же 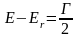, то:

Таким образом, чтобы по известному графику найти ширину уровня Г, надо взять ширину резонанса на половине высоты резонанса.

3) интересен случай при E << E_r (вдали от резонанса), при этом

где v_n - скорость нейтрона.

Для многих ядер в области тепловой энергии нейтронов зависимость сечения взаимодействия от энергии пропорциональна 1/v_n.