18. Управление реактором

    1. Нарушение нейтронного баланса

Чтобы реактор работал длительное время на заданной мощности, необходимо, чтобы в течение этого времени К_эфф=1. Однако в энергетическом реакторе существуют причины, приводящие к уменьшению К_эфф:

1. выгорание делящегося вещества;

2. образование ядер-осколков, хорошо поглощающих нейтроны деления;

3. температурные эффекты.

Если в начале работы К_эфф=1, то уже через малый промежуток времени стало бы К_эфф<1, и реакция прекратилась бы. Поэтому собирают активную зону с К_эфф>1(обычно 1.12) и помещают достаточное количество компенсирующих регулирующих стержней так, чтобы К_эфф=1. По мере выгорания топлива падение К_эфф компенсируется выдвижением стержней. При этом стремятся к тому, чтобы вес отдельного стержня был . Количество регулирующих стержней примерно равно

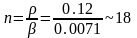
После изъятия последнего компенсирующего стержня по истечении периода работы реактор останавливается из-за недостатка реактивности.

2. Регулирующие стержни

Регулирующие стержни изготовляют из Cd¹¹³ или B¹⁰ - это изотопы, которые имеют очень большое сечение поглощения. Сечение поглощения при тепловой энергии нейтронов

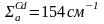
 =0.01см

Слой Cd в 1мм. практически полностью поглощает нейтронный поток. Для быстрых реакторов применяют стержни из В (бора).

Классификация регулирующих стержней:

1. компенсирующие, их вводят в активную зону вначале и постепенно вынимают, по мере снижения запаса реактивности;

2. стержни ручного регулирования (РР), ими пользуются операторы при работе для перехода с одного уровня сложности на другой;

3. стержни автоматического регулирования (АР) – поддерживают точно критическое состояние реактора, они работают непрерывно, реагируя на любое колебание параметров;

4. стержни аварийной защиты (АЗ) регулируют в случае аварийной ситуации, когда имеются отклонения от номинальных параметров.

Схема стержня

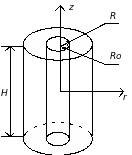
Рис. 18.2.1.

Оценим вес стержней. Рассмотрим цилиндрический реактор с полностью введенным поглощающим стержнем. Будем считать, что введение стержня связано с вытеснением горючего вещества из реактора. Это характерно для реактора бассейного типа.

Поглощающий стержень из Cd можно считать абсолютно черным. Найдем эффективность, т.е. коэффициент размножения со стержнем и без него. Т.к. мы уже находили параметры реактора без стержня, то найдем условия критичности для реактора со стержнем.

Граничные условия:

=0 на экстраполированной границе вблизи R

=0 на экстраполированной границе вблизи R₀;

здесь граница не плоская, и длина экстраполяции при r0 равна

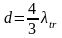
Т.о. эффективный радиус стержня

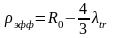
Итак, ГУ:

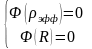
Для реактора любой формы в стационарном случае выполняется уравнение

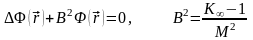
Будем считать, что все нейтроны рождаются, диффундируют и поглощаются при одной энергии. Однако будем пользоваться площадью миграции M², т.е. учтем замедление. Для цилиндрического реактора имеем

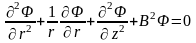
Будем искать решение в виде (r, z)=(r)Z(z)

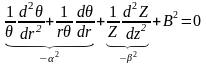
B²⁼²+²

Рассмотрим радиальное распределение потока (r)

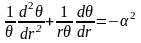
Или

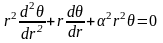
А это есть уравнение Бесселя. Его решение

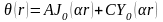
Распределение J(x)

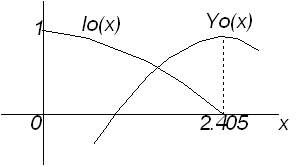
Рис. 18.2.2.

При х0 Y₀-∞, когда рассматривается активная зона без отражения, можно полагать С=0. Центр зоны также не рассматривается, т. к. точка r=0 не входит в область определения потока  из-за поглощающего стержня в центре.

ГУ:

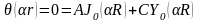
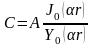
А – пропорционально мощности реактора и может быть найдено только из задания мощности. Значит решение

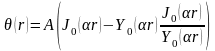
При r=_эфф имеем условие

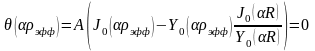
которое выполняется для любого A, если

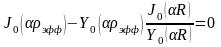
Это и есть условие критичности для цилиндрического реактора со стержнем. Стационарное решение существует только в том случае, если α (материальный параметр, характеристика ядерных свойств среды) – корень данного уравнения. α должно быть совершенно определёно

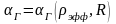
Чтобы определить вес стержня, необходимо получить геометрический параметр реактора со стержнем α_Г. Этот параметр не сильно отличается от геометрического параметра реактора без стержня α₀. Предположим, что стержень слабо возмущает реактор (имеет малый вес), тогда изменение геометрического параметра из-за введения стержня тоже можно считать малым.

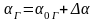
где 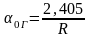- без стержня;

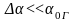
Из условия критичности найдем 

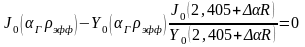
Функции Бесселя можно разложить вблизи корня 2,405 по малому параметру :

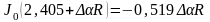
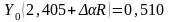
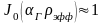, т. к.

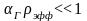
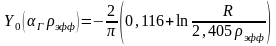
Подставим это в условие критичности

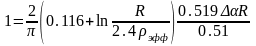
Отсюда

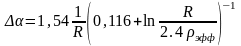
C учетом малого возмущения, т.е. пользуясь формулой для невозмущенного реактора, можно записать

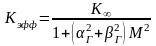
Учтем, что для критического реактора

,

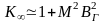и запишем изменение К_эфф из-за малого возмущения

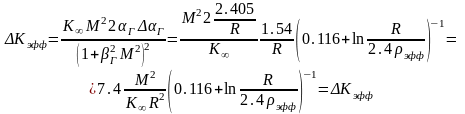
К_эфф и есть оценка веса стержня. Пусть задан водный реактор

М²≈30см; R≈100см; 2,4_эфф=1см.

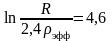
Период разгона будет не слишком мал. Нужно следить, чтобы вес одного стержня не был больше . Зависимость от радиуса стержня достаточно слаба.

Сечение стержня

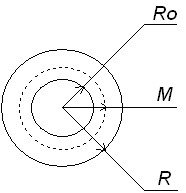
Рис. 18.2.3.

Вокруг стержня можно выделить область радиусом M (М – длина миграции). Нейтроны, рождающиеся в этой области, имеют большую вероятность поглотиться в стержне. Нейтроны, рожденные вне этой области, практически не могут быть поглощены стержнем. Поэтому эффективность должна определяться отношением объема зоны, в которой велико влияние стержня, к общему объему реактора.

Имеем распределение потока в радиальном направлении в виде:

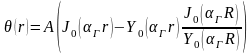
Регулирующий стержень деформирует распределение нейтронного потока в реакторе так, что увеличивается нейтронный поток на периферии. Значит, введение стержня увеличивает утечку нейтронов из реактора.

Зависимость (r)

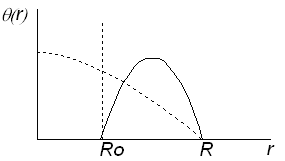
Рис. 18.2.4.