1. 0000Основные понятия теории реакторов

В 1938 году была открыта реакция деления урана с выделением энергии. Но практически применение этой энергии стало возможным лишь путем осуществления цепной ядерной реакции в широких масштабах.

Ядерным реактором называется установка, в которой в большом масштабе осуществляется реакция деления ядер под воздействием нейтронов. В результате этой реакции выделяется энергия.

Теория ядерных реакторов распадается на две части:

1. Теория ядерных процессов, которые происходят в реакторе. Эта теория связана с расчетом сечения ядерных реакций, иначе говоря, с расчетом вероятности взаимодействия нейтронов с ядрами среды реактора. Эта теория широко использует квантовую механику.

2. Теория распространения и размножения нейтронов в среде. Эта теория носит классический характер и может быть изложена без ссылок на существо ядерных реакций.

Необходимо знать только сечения взаимодействия, которые определяются экспериментально и содержатся в справочниках. Движение нейтрона от ядра к ядру можно представить классическим, а что происходит при взаимодействии нейтрона и ядра пока не важно, надо только знать вероятности различных временных реакций нейтрона с ядром и вероятности приобрести после столкновения некоторую скорость V.

1. 0000Простейший ядерный реактор

Содержание теории ядерных реакторов легче всего понять на примере простейшего реактора ­- сферы из делящегося изотопа ²³⁵U. Диаметр этой сферы, в которой может осуществляться незатухающая цепная реакция, составляет 10 см. Нейтроны имеют очень малое сечение взаимодействия с электронами и поэтому не чувствуют электронных оболочек атома. Решетка ²³⁵U имеет шаг, равный 10^-8 см, а диаметр ядра 10^-12 см. Ядра занимают ничтожную часть объема, занимаемого веществом. Для нейтрона твердое тело представляет собой некоторое решето, через которое он сравнительно легко проходит. Средняя длина свободного пробега имеет порядок 1 см. Таким образом, простейший реактор представляет собой совокупность распространенных в пространстве ядер ²³⁵U и хаотически двигающихся между ними нейтронов, изредка сталкивающихся с ядрами.

Какие реакции происходят при столкновении нейтрона и ядра? Наиболее важными являются следующие ядерные реакции изотопа ²³⁵U с нейтронами:

1. Реакция поглощения нейтрона с последующим делением:

U²³⁵+ n₀ ® (U²³⁶)^* ® 

® (2 осколка деления) + (n нейтронов) + (b -частица) + (g-квант),

n = 1 – 6 ,

Вероятность – 84%.

2. Реакция радиационного захвата:

U²³⁵ + n₀ ® (U²³⁶)^* ® U²³⁶ + (g -квант)

Вероятность – 16%.

Возбужденное ядро U²³⁵ может излучить энергию в виде g-кванта и упасть на основной уровень. Вероятность возбужденного ядра (U²³⁶)^* претерпеть распад = 0,84, а излучить g‑квант = 0,16

3. Реакция рассеяния:

U²³⁵ + n₀ ® U²³⁵ + n₀

Нейтрон и ядро как шарики сталкиваются и разлетаются. При этом меняется направление и модуль скорости полета нейтрона. Зная возможные реакции нейтрона с ядрами, рассмотрим поведение нейтрона, родившегося в результате деления одного из ядер ²³⁵U. Нейтроны при делении испускаются с энергией ~ 2 МэВ (0.32 кДж). Энергия нейтрона в 10⁷ раз превышает среднюю энергию колеблющихся ядер, до другого нейтрон перемещается по прямой линии, а в целом его траектория будет ломаной линией. Нейтрон будет двигаться по среде до тех пор, пока не будет захвачен каким-либо ядром или не выйдет за пределы сферы. В теории реакторов принято считать, что вне сферы находится вакуум, и вылетевший нейтрон считается потерянным, так как он не может возвратиться в рассматриваемую систему.

Таким образом, каждый рожденный нейтрон имеет две характерных траектории, две возможности:

1. поглотиться в U²³⁵

2. покинуть реактор

Утечка нейтронов

а)

b)

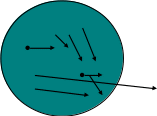
Рис. 1.1.1. 

При делении ядра урана образуется от одного до шести нейтронов, рис. 1.1.1. но нас интересует среднее число нейтронов на один акт деления, будем его обозначать через n. Она зависит от энергии поглощенного нейтрона и вида делящегося изотопа. Для U²³⁵ для тепловых нейтронов n = 2.47. Полезно ввести еще одну характеристику процесса деления: h - среднее число нейтронов, образующихся в результате поглощения одного нейтрона ядром U²³⁵.

Какая из введенных величин больше? Очевидно, что h < n вследствие радиационного захвата, вследствие того, что не каждый поглощаемый в U²³⁵ нейтрон вызывает деление ядра (для U²³⁵ h  = 2,07). Необходимо выяснить в каком случае возможно развитие стационарной, незатухающей реакции в простейшем реакторе. Для этого проследим за судьбой некоторого числа нейтронов.

Пусть в некоторое мгновение во всем реакторе поглотилось Q нейтронов. На каждый поглощенный нейтрон рождается в среднем h нейтронов. Следовательно, если Q поглотилось в одном поколении, то Qh нейтронов родилось. Родившиеся нейтроны имеют две возможности:

а) поглотиться в реакторе в следующем поколении, причем количество таких нейтронов будет равно QηP;

б) утечь из реактора: Qh(1 ‑ P) – количество покинувших реактор,

где P - вероятность избежать утечки, усредненная по всем нейтронам, т.е. по всем точкам рождения и направлениям скорости.

Для удобства вводят характеристику разложения нейтронов - коэффициент размножения. Коэффициентом размножения называют отношение числа нейтронов одного поколения к соответствующему числу нейтронов предыдущего поколения (нужно рассматривать нейтроны не одной и той же стадии существования).

В нашем случае

K_эф = Qh P/Q = h P; K_эф = h P.

Для экспериментаторов особый интерес представляет случай стационарной работы ядерного реактора, когда поток нейтронов и соответственно мощность остаются постоянными. Отношение числа нейтронов в двух последующих поколениях в этом случае равно 1, то есть K_эф = ηP = 1.

Реактор, работающий в стационарном режиме, называется критическим, а условием критичности является вышеуказанное равенство.

Реактор может находиться в режиме убывания нейтронного потока, когда k_эф < 1. Такой реактор называют подкритичным. Реактор может находиться в режиме нарастания нейтронного потока, когда k_эф > 1. Такой реактор называют надкритичным.

Каким образом можно достигать критичности? Из нашей формулы ясно, что необходимо варьировать либо h, либо вероятность P избежать утечки. Величина η связана с составом активной зоны реактора. Критичности можно достичь, меняя состав реактора, но в этом направлении наши возможности ограничены определенными свойствами имеющихся делящихся веществ. P - вероятность избежать утечки характеризует соотношение вероятностей поглотиться в реакторе и утечь из него. Поглощение - эффект объемный, вероятность поглощения ~ объёму V, а вероятность утечь ~ площади S, поэтому для шара радиусом R

.

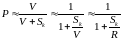Чем больше R, тем больше P. Т.е. очевидно, что при заданном составе активной зоны может существовать такой размер, при котором реактор становиться критическим. Такой размер также носит название критичного. P не может превысить 1 и поэтому ясно, что не любую активную зону можно сделать критической, а только ту, у которой h > 1.