Лабораторная работа №5

Аппроксимация

Цель работы: изучить основные возможности приложения Microsoft Excel 2010 для аппроксимации экспериментальных данных.

5.1. Краткие теоретические сведения

В инженерной практике часто приходиться иметь дело с таблицей численных значений экспериментальных данных, отражающих некоторую функциональную зависимость y_i = f(x_i). С численными значениями такой зависимости в большинстве случаев работать неудобно, поэтому с помощью различных методов пытаются подобрать такую формулу

y = φ(x), график которой наиболее точно отражает зависимость y_i = f(x_i). Такая замена табличных значений зависимости y_i = f(x_i) аналитической функцией y = φ(x) называется аппроксимацией, а функция φ(x) – аппроксимирующей функцией.

С одной стороны, для удобства работы с аппроксимирующей функцией она должна быть как можно более простой, с другой – увеличение точности аппроксимации требует применения более сложной аппроксимирующей функции. Поэтому задача аппроксимации в общем случае является творческой и во многих случаях ее успешное решение зависит как от характера зависимости y_i = f(x_i), так и от знаний и опыта инженера.

На практике чаще всего в качестве простейших аппроксимирующих функций используют:

• линейную y = φ(x) = ax + b; (1)

• степенную y = φ(x) = ax^b; (2)

• логарифмическую y = φ(x) = aln(x) + b; (3)

• экспоненциальную y = φ(x) = ae^bx. (4)

Как нетрудно видеть, функции (1) – (4) содержат всего по два коэффициента аппроксимации: a и b. Если эти функции не обеспечивают требуемой точности аппроксимации, количество коэффициентов необходимо увеличить и использовать более сложные функции. В большинстве случаев переходят к использованию полиномиальной аппроксимации

y = φ(x) = a₀ + a₁x + a₂x² + a₃x³ + … + a_nxⁿ. (5)

Применение полиномиальной аппроксимации (5) позволяет путем увеличения степени полинома и, соответственно, количества коэффициентов повысить точность аппроксимации.

Для оценки точности аппроксимации используется коэффициент корреляции Пирсона, который вычисляется по формуле

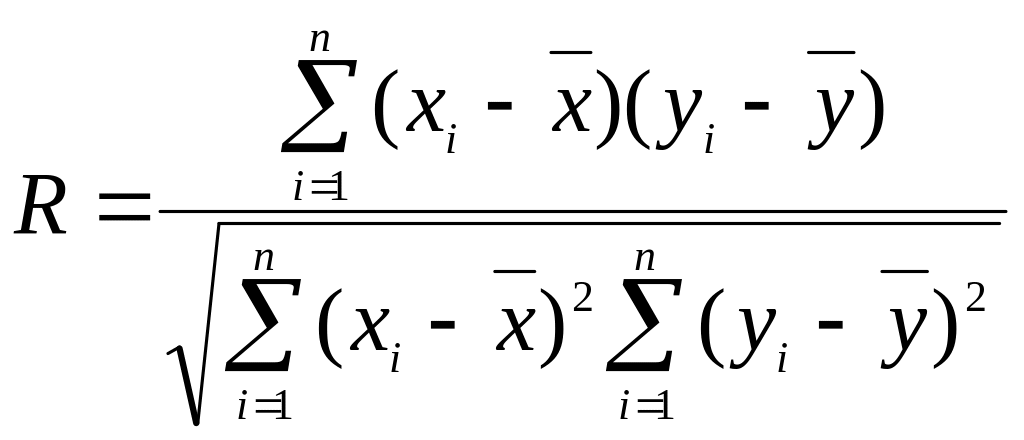. (6)

В приложении Microsoft Excel для оценки точности аппроксимации используется квадрат коэффициента корреляции (6) – достоверность аппроксимации R². Чем величина R² ближе к единице, тем аппроксимация точнее.

5.2. Пример

Используя все виды функций (1) – (5) аппроксимировать экспериментальную зависимость y_i = f(x_i), представленную таблицей

Таблица 5.1

Экспериментальные данные

Xi	1	3	4	5	6	8	10	11	12	13	14
Yi	11	21	30	45	55	68	78	83	86	89	92

Пользуясь величиной достоверности аппроксимации R² найти наилучшую среди аппроксимирующих функций (1) – (4), имеющих по два коэффициента, и сравнить ее с полиномиальной аппроксимацией (5). Сделать выводы.

Методические рекомендации

1. Запустите приложение Microsoft Excel 2010: Пуск → Все программы → Microsoft Office → Microsoft Excel 2010. В окне Excel откроется новая рабочая книга с тремя листами.

2. Сохраните рабочую книгу в своей рабочей папке на диске или на личном внешнем носителе: вкладка Файл – команда Сохранить как. Дайте имя файлу Л.р.№5-пример.

3. Замените имя текущего рабочего листа. Для этого дважды щелкните левой кнопкой мыши по ярлычку рабочего листа с надписью Лист1 и наберите имя листа Данные.

4. Занесите в строку 1 значения X_i из таблицы 5.1. а в строку 2 – значения Y_i, как показано на рисунке 5.1.

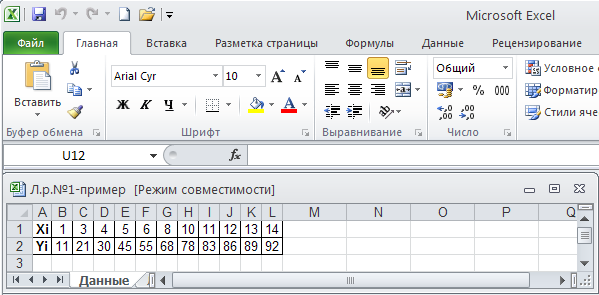
Рис. 5.1. Таблица с данными

5. Сохраните рабочую книгу. Для сохранения книги под своим текущим именем используется кнопка с пиктограммой в левом верхнем углу (Панель быстрого доступа), или команда Сохранить вкладки Файл.

Рекомендация! Чтобы избежать потери данных в аварийных ситуациях, связанных, например, с выключением питания, зависанием компьютера и т. д., сохраняйте файл после каждого успешного действия.

6. Пользуясь этими данными, постройте диаграмму. Для построения диаграммы выделите диапазон ячеек с данными A1:L2, перейдите на вкладку Вставка, в группе Диаграммы укажите тип Точечная и выберите вид диаграммы Точечная с маркерами. Диаграмма появится на текущем листе Данные.

7. Переместите построенную диаграмму на другой лист. Для этого перейдите на вкладку Расположение и укажите Переместить диаграмму. В диалоговом окне Перемещение диаграммы установите переключатель в положение на имеющимся листе:, откройте выпадающий список и выберите Лист2.

8. Отредактируйте построенную диаграмму. Для этого наведите курсор мыши на любую линию сетки и дождитесь всплывающей подсказки Вертикальная ось (значений) – основные линии сетки. Нажмите правую кнопку мыши и в меню укажите пункт Удалить. С правой стороны диаграммы располагается элемент диаграммы Легенда, который при наличии одного графика на диаграмме, не имеет смысла. Для удаления легенды наведите курсор на изображение легенды, дождитесь появления всплывающей подсказки «Легенда», или «Ряд Y_i Элемент легенды», выделите легенду и нажмите клавишу Delete на клавиатуре.

9. Наведите курсор мыши на любую точку построенного графика, дождитесь появления всплывающей подсказки с параметрами этой точки и нажмите правую клавишу мыши. В появившемся меню укажите пункт Добавить линию тренда… и нажмите левую клавишу мыши.

10. В появившемся диалоговом окне Формат линии тренда в панели Параметры линии тренда установите переключатель в положение Линейная, а также установите переключатели показывать уравнение на диаграмме и поместить на диаграмму величину достоверности аппроксимации(R^2) в положение включено и нажмите на кнопку Закрыть.

11. Назовите лист с диаграммой Линейная.

12. Переместите уравнение на свободное место диаграммы, подберите размер шрифта, тип линии тренда и параметры маркера таким образом, чтобы изображение имело вид, как показано на рисунке 5.2.

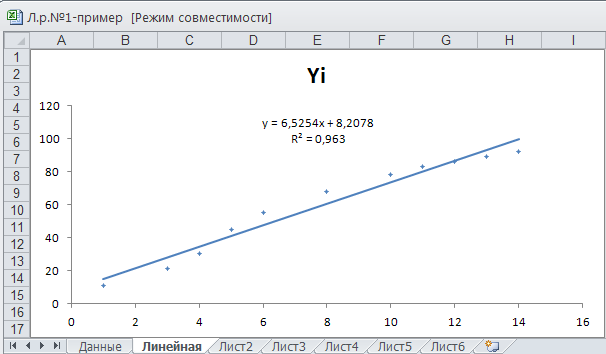
Рис. 5.2. Диаграмма с линейной аппроксимацией

13. Выполните еще раз пункты 6 – 9 и постройте на отдельном листе диаграмму со степенной аппроксимацией (2). Назовите лист с диаграммой Степенная и отредактируйте диаграмму как показано на рисунке 5.3.

Рис. 5.3. Диаграмма со степенной аппроксимацией

14. Выполните еще раз пункты 6 – 9 и постройте на отдельном листе диаграмму с логарифмической аппроксимацией (3). Назовите лист с диаграммой Логарифмическая и отредактируйте диаграмму как показано на рисунке 5.4.

15. Выполните еще раз пункты 6 – 9 и постройте на отдельном листе диаграмму с экспоненциальной аппроксимацией (4). Назовите лист с диаграммой Экспоненциальная и отредактируйте диаграмму как показано на рисунке 5.5.

Рис. 5.4. Диаграмма с логарифмической аппроксимацией

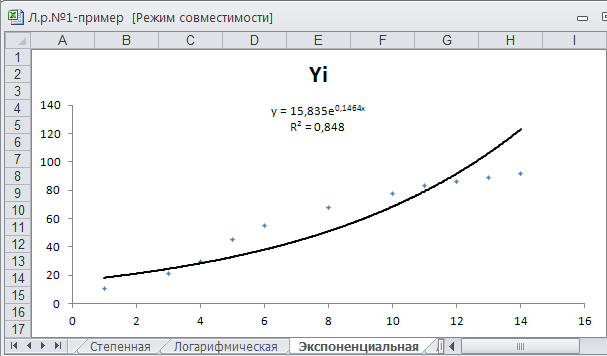
Рис. 5.5. Диаграмма с экспоненциальной аппроксимацией

16. Выполните еще раз пункты 6 – 9 и постройте на отдельном листе диаграмму с полиномиальной аппроксимацией (5). При выполнении полиномиальной аппроксимации постройте несколько графиков линиями различного цвета, увеличивая степень полинома от 2 до 4. Сделайте так, чтобы уравнение и соответствующий ему график были одинакового цвета.

17. Назовите лист с диаграммой Полиномиальная и отредактируйте диаграмму как показано на рисунке 5.6.

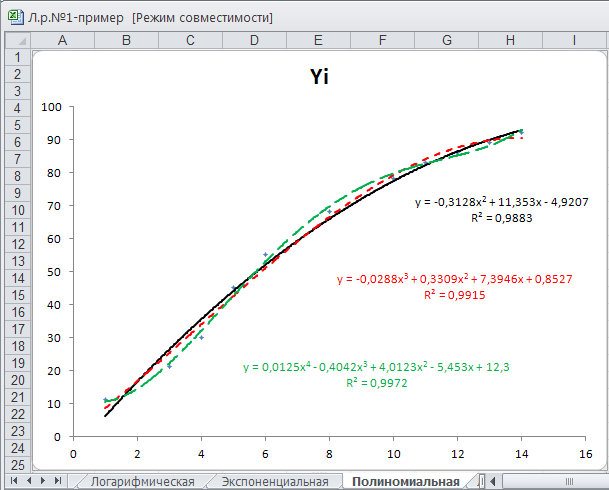
Рис.5.6 Диаграмма с полиномиальной аппроксимацией

Выводы

1. Анализ результатов, представленных на рисунках 5.2 – 5.5 показывает, что наибольшая точность в случае использования аппроксимирующих функций с двумя коэффициентами (1) – (4) обеспечивается степенной аппроксимацией (2), где R²=0,9752.

2. Как следует из рисунка 5.6, применение полиномиальной аппроксимации (5) обеспечивает более высокое значение R². Так, при использовании полинома второй степени с тремя коэффициентами R²=0,9883. Использование полиномов с еще большим количеством коэффициентов приводит к дальнейшему увеличению точности аппроксимации.