Задание №4. Выявление основной тенденции развития рядов динамики методом укрупнения интервалов и скользящих средних.

Условие задачи: Имеются следующие данные о реализации молочной продукции в магазинах города по месяцам с 2004 — 2007 г.г. (тыс.т.), представленные на рис.4.

Для изучения общей тенденции реализации данной продукции необходимо:

1. Произвести преобразование исходных данных путём укрупнения периодов времени: а) в квартальные уровни, б) в годовые уровни;

2. Построить линейный график квартальных уровней;

3. Произвести сглаживание квартальных уровней с применением пятизвенной скользящей средней;

4. Построить график пятизвенной скользящей средней.

5. Сделать выводы о характере основной тенденции изучаемого явления.

Ход выполнения:

1. В книгу Ряды динамики.xls добавьте новый лист и переименуйте его в лист Задание 4.

2. Создайте таблицу согласно рис.4.

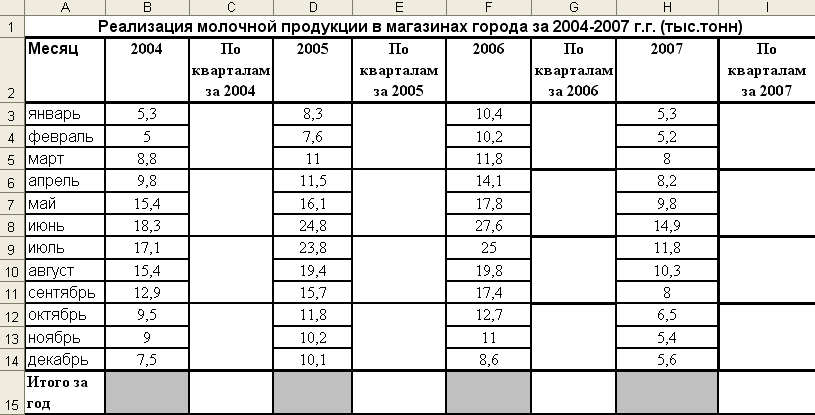
Рис.4. Данные для задания №4.

3. Произведите преобразование исходных данных путём укрупнения периодов времени в годовые уровни, рассчитав объемы продаж за 2004-2007 г.г. в соответствующих ячейках.

4. Произведите преобразование исходных данных путём укрупнения периодов времени в квартальные уровни, рассчитав объемы продаж по кварталам за 2004-2007 г.г. в соответствующих ячейках.

5. Постройте ряд динамики квартальных уровней в диапазоне ячеек А18: С34 согласно рис. 5, добавив в столбец С рассчитанные квартальные объемы продаж.

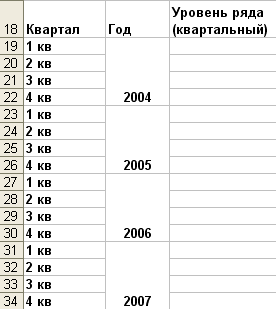
Рис.5. Ряд динамики (по кварталам)

6. На основании квартальных уровней постройте диаграмму (тип – график), отражающую ряд динамики.

7. Произведите сглаживание квартальных уровней с применением пятизвенной скользящей средней, используя функцию СРЗНАЧ в диапазоне ячеек D19:D34.

8. Произведите сглаживание квартальных уровней с применением пятизвенной скользящей средней, используя инструмент анализа Скользящее среднее. Для этого:

   • Выполните команду Сервис/Анализ данных.

   • Выберите инструмент Скользящее среднее.

   • В диалоговом окне установите параметры согласно рис. 6.

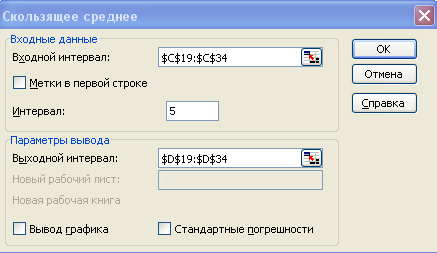
Рис. 6. Диалоговое окно «Скользящее среднее».

9. Постройте график пятизвенной скользящей средней, добавив новый ряд на уже существующий график (см. рис.7).

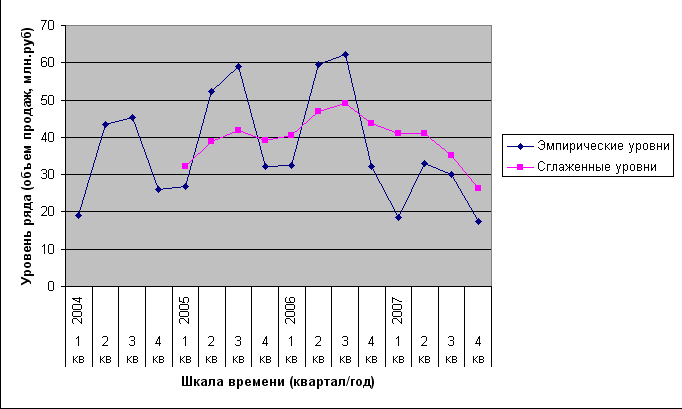
Рис.7. Графики ряда динамики и скользящей средней.

10. Сделайте вывод о характере основной тенденции развития изучаемого явления.

11. Сохраните изменения в книге Ряды динамики.xls.

4.3. Метод аналитического выравнивания.

Применение в анализе рядов динамики методов укрупнения интервалов и скользящей средней позволяет выявить тренд (тенденцию) для его описания, но получить обобщенную статистическую оценку тренда посредством этих методов невозможно. Решение этой более высокого порядка задачи – измерения тренда – достигается методом аналитического выравнивания.

Основным содержанием метода аналитического выравнивания в рядах динамики является то, что основная тенденция развития рассчитывается как функция времени

ŷ_{t =} ƒ (t_i) (4.4)

Определение теоретических (расчетных) уровней ŷ_{t производится на основе так называемой адекватной математической} функции, которая наилучшим образом отображает основную тенденцию ряда динамики. Подбор адекватной функции осуществляется методом наименьших квадратов, сущность которого заключается в минимизации суммы квадратов отклонений между эмпирическими y_i и теоретическими ŷ_{t уровнями:}

= (y_i - ŷ_t )² = min (4.5)

Важнейшей проблемой, требующей своего решения при применении метода аналитического выравнивания, является подбор математической функции, по которой рассчитываются теоретические уровни тренда. От правильности решения этой проблемы зависят выводы о закономерностях тренда изучаемых явлений. Если выбранный тип математической функции адекватен основной тенденции развития изучаемого явления во времени, то синтезированная на его основе трендовая модель может иметь полезное применение при изучении сезонных колебаний, прогнозировании и других практических целях.

Одним из условий обоснованного применения метода аналитического выравнивания в анализе рядов динамики является знание типов развития социально-экономических явления во времени, их основных отличительных признаков. В практике статистического изучения тренда различают следующие эталонные типы развития социально-экономических явлений во времени.

1. Равномерное развитие. Для этого типа развития присущи постоянные цепные абсолютные приросты:

(4.6)

Основная тенденция развития в рядах динамики со стабильными абсолютными приростами отображается уравнением прямолинейной функции.

(4.7)

где a₀ и a₁ – параметры уравнения; t – время.

Параметр a₀ является коэффициентом регрессии, определяющим направление развития. Если a₁ > 0, то уровни ряда динамики равномерно возрастают, а при a₁ < 0 происходит их равномерное снижение.

Если в формуле (4.5) вместо ŷ_t подставить , то получим:

(4.8)

Это функция двух переменных (все и известны), которая при определенных достигает минимума. Из этого выражения на основе знаний, полученных в курсе высшей математики об экстремуме функций n переменных, получают значения коэффициентов .

(4.9)

(4.10)

где n — число моментов времени, для которых были получены исходные уровни ряда .

Если вместо абсолютного времени выбрать условное время таким образом, чтобы , то записанные выражения для определения упрощаются:

(4.11) и (4.12)

2. Равноускоренное (равнозамедленное) развитие. Этому типу динамики свойственно постоянное во времени увеличение (замедление) развития. Уровни таких рядов динамики изменяются с постоянными цепными темпами прироста:

(4.13)

Основная тенденция развития в рядах динамики со стабильными темпами прироста отображается функцией параболы второго порядка:

(4.14)

В формуле (4.9) параметры a₀ и a₁ идентичны параметрам, используемым в формуле (4.7). Параметр a₂ характеризует постоянное изменение интенсивности развития (в единицу времени).

Если a₂ > 0, то происходит ускоренное развитие, а при a₂ < 0 идет процесс замедления роста.

3. Развитие с переменным ускорением (замедлением). Для этого типа динамики основная тенденция развития отображается функцией параболы третьего порядка:

(4.15)

В формуле (4.10) параметр a₃ отображает изменение ускорения. Если a₃ > 0, то ускорение возрастает, при a₃ < 0 ускорение замедляется.

4. Развитие по экспоненте. Этот тип динамики характеризует стабильные цепные темпы роста:

(4.16)

Основная тенденция развития в рядах динамики с постоянными темпами роста отображается показательной функцией:

(4.17)

где a₁ - темп роста (снижения) изучаемого явления в единицу времени, т.е. интенсивность развития.

5. Развитие с замедлением роста в конце периода. У этого типа динамики показание цепного абсолютного прироста сокращается в конечных уровнях ряда динамики:

(4.18)

Основная тенденция развития в таких рядах динамики отображается полулогарифмической функцией:

(4.19)

При аналитическом выравнивании в рядах динамики можно применять и другие математические функции. Так, при изучении основной тенденции развития неудовлетворенного и реализованного спроса населения применяются

Степенная функция: (4.20)

Функция гиперболы: (4.21)