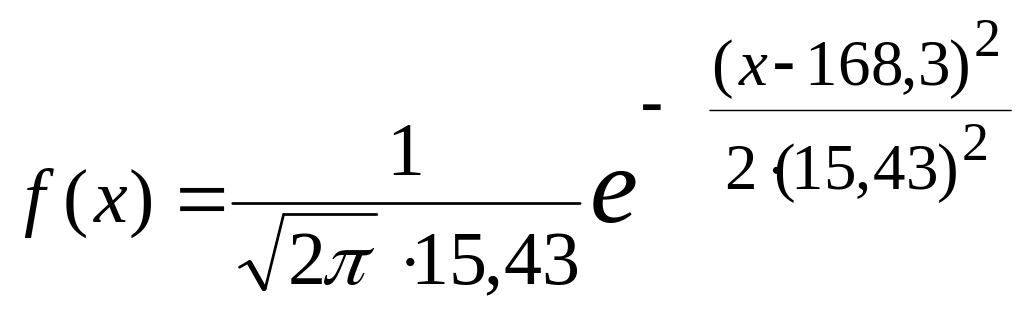2. Задание к расчёТно – графической работе

Задача 1. Расчет основных статистических показателей и их оценка в большой выборке. Проверка статистических гипотез о законе распределения генеральной совокупности.

1. Записать данные наблюдения согласно полученному заданию.

2. Выполнить сводку данных наблюдения и построить статистическое распределение выборки.

3. Построить полигон и гистограмму. По виду гистограммы (или полигона) выдвинуть гипотезу о законе распределения исследуе­мой случайной величины.

4. Вычислить основные статистические показатели: выборочную среднюю, выборочную дисперсию, среднее квадратическое отклоне­ние и коэффициент вариации. Для нормального распределения найти показатели мер косости и крутости.

5. Вычислить ошибки полученных статистических показателей и оце­нить их достоверность на 5 %-ном уровне значимости.

6. Проверить по критерию согласия Пирсона (критерию χ²) выдви­нутую гипотезу о законе распределения. Построить график теоре­тической плотности распределения.

7. Для нормального распределения найти доверительные интервалы среднего значения, среднего квадратического отклонения и коэффициента вариации в генеральной совокупности на 5 %-ном уровне значимости.

8. Провести анализ результатов и сделать выводы.

Задача 2. Расчет основных статистических показателей большой выборки с помощью пакета Mathсad на ЭВМ.

1. Ознакомиться с программой на языке Mathсad для расчета основных статистических показателей, приведенной в приложении 5.

2. Ввести исходные данные согласно варианту.

3. Провести расчет основных статистических показателей.

4. Построить графики эмпирической и теоретической кривой нормального распределения.

5. Провести анализ полученных результатов и сравнить их с данными, полученными при «ручном расчете».

3. Образец выполнения задания

Задача 1

1. Данные наблюдения

В качестве примера рассмотрим результаты измерения роста случайно отобранных 100 студентов НГМА, см:

164	150	171	186	185	192	137	165	183	153
158	144	142	154	157	138	160	162	170	163
163	163	187	167	165	161	196	180	201	159
191	145	176	181	195	167	161	177	163	179
148	156	147	163	168	168	163	199	144	158
132	188	150	159	179	175	180	176	149	152
178	173	155	165	170	176	170	155	194	175
169	180	180	159	155	184	151	146	178	177
199	188	186	170	168	174	168	153	143	180
174	177	171	154	185	164	156	157	162	162

Выборочная совокупность содержит результаты 100 наблюдений и поэтому она является большой выборкой. Кроме того, среди значений встречаются повторяющиеся варианты. Обработка таких совокупностей достаточно трудоёмкая, имеющиеся закономерности распределения трудно или даже не возможно уловить. Поэтому полученные экспериментальные данные подвергают обработке: группируют отдельные наблюдения в интервалах и располагают их в порядке возрастания. Это действие называют сводкой данных наблюдения, в результате чего получают интервальный вариационный ряд.

1. Для выполнения сводки данных измерения роста случайно отобранных 100 студентов необходимо все данные разбить на k интервалов одинаковой длины. Число интервалов определяют по приближенной формуле Стерджесса:

(21)

где - объем выборки. Число интервалов округляем до целого числа. В нашем примере

Длину интервала определяют так: (22)

Где - наибольший элемент выборки; - наименьший элемент выборки.

Длину интервала вычисляют с точностью выборки. В нашем примере:

(см). Тогда (см)

Границы интервалов вычисляем по формуле:

(23)

После определения границ интервалов производят сводку данных наблюдений с помощью рабочей таблицы 1, состоящей из трех столбцов. В первый столбец заносят полученные выше интервалы. Во втором столбце отмечается каждое значение из выборки путем постановки черточки против соответствующего интервала, причем значение, совпадающее с границей интервала, относят к тому интервалу, для которого оно является левой границей. В третий столбец записывается сумма черточек каждой строки таблицы, которая является частотой того или иного варианта.

Таблица 1 – Сводка данных наблюдения

Интервалы	Сводка	Частота
132 - 141	|||	3
141 - 150		9
150 - 159		17
159 - 168		22
168 - 177		19
177 - 186		17
186 - 195		8
195 - 204		5
		åni=100

Интервальный ряд распределения, полученный по сводке данных наблюдения, запишем в виде таблицы 2.

Таблица 2 – Интервальный ряд распределения частот

Интервалы (рост студентов, см)	132 - 141	141 - 150	150 - 159	159 - 168	168 - 177	177 - 186	186 - 195	195 - 204
Частота	3	9	17	22	19	17	8	5

Ряд распределения (статистический ряд) характеризуется значением вариант, представляющих собой величины середин каждого интервала и соответствующих им частот. Тогда ряд распределения можно записать в виде таблицы 3 и таблицы 4.

Таблица 3 – Статистический ряд распределения частот

Значение (см)	136,5	145,5	154,5	163,5	172,5	181,5	190,5	199,5
Частота	3	9	17	22	19	17	8	5

Таблица 4 – Ряд распределения относительных частот

Значение (см)	136,5	145,5	154,5	163,5	172,5	181,5	190,5	199,5
Относительная частота	0,03	0,09	0,17	0,22	0,19	0,17	0,08	0,05

Результат обработки выборочной совокупности, представленный таблицей 3, называется статистическим рядом распределения частот признака (рост студентов, см), а в виде таблицы 4 – рядом распределения относительных частот этого же признака.

2. Для построения гистограммы относительных частот необходимо знать длины интервалов 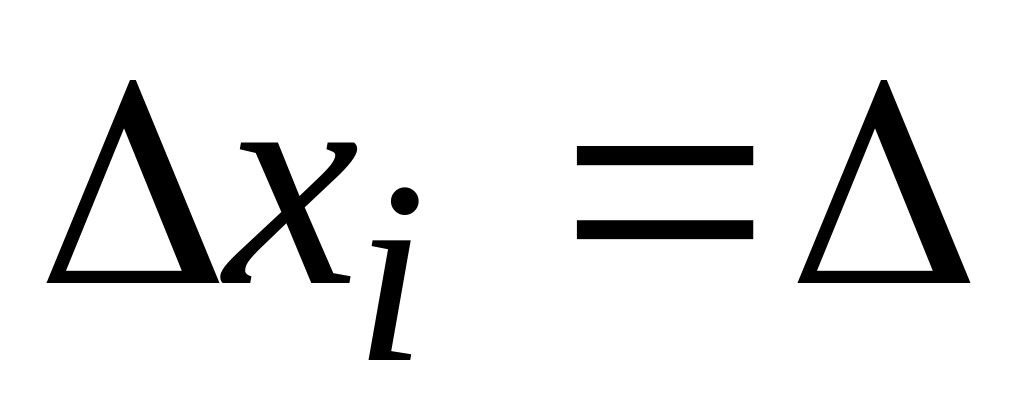(основания прямоугольников) и высоты (плотность относительной частоты). Все необходимые данные занесем в таблицу 5.

Таблица 5 – Ряд распределения плотности относительной частоты

Значение (см)	136,5	145,5	154,5	163,5	172,5	181,5	190,5	199,5
Плотность	0,003	0,010	0,019	0,024	0,021	0,019	0,008	0,005

По таблице 5 строим гистограмму относительных частот (рисунок 1). Соединяя середины верхних сторон прямоугольников отрезками прямых линий, получаем полигон относительных частот (штриховая линия).

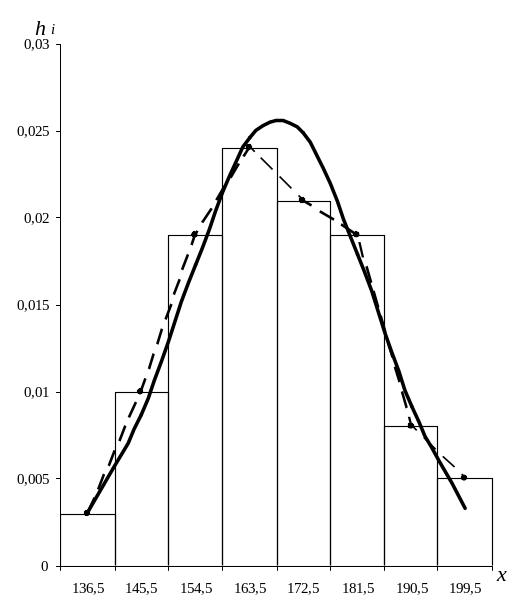
Рисунок 1 – Полигон и гистограмма относительных частот. Теоретическая кривая нормального распределения.

По виду гистограммы (полигона) выдвигаем гипотезу о нормальном распределении роста студентов.

3. Вычислим основные статистические показатели с помощью рабочей таблицы 6:

Таблица 6 – Расчет основных статистических показателей

	ni
1	2	3		4	5	6	7	8
136,5	3	409,5		–31,77	–95,31	3028	–96200	3056000
145,5	9	1310		–22,77	–204,93	4666	–106300	2419000
154,5	17	2627		–13,77	–234,09	3223	–44390	611200
163,5	22	3597		–4,77	–104,94	500,564	–2388	11390
172,5	19	3277		4,23	80,37	339,965	1438	6083
181,5	17	3086		13,23	224,91	2976	39370	520800
190,5	8	1524		22,23	177,84	3953	87880	1954000
199,5	5	997,5		31,23	156,15	4877	152300	4756000
Σ	100	1,683∙104			0	2,356∙104	3,176∙104	1,333∙107

Заполнив третью колонку таблицы, вычисляем среднее выборочное по формуле (1):

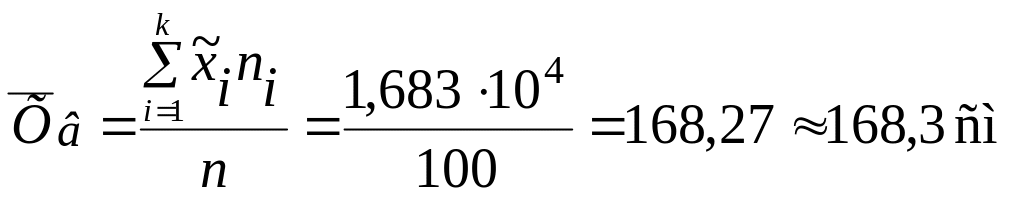
среднее выборочное округляем до размерности выборки. Остальные числовые характеристики будем округлять на порядок точнее.

Найдя , заполняем остальные столбцы таблицы построчно. Для этого значение из 4-го столбца умножаем на значение 2-го столбца, стоящее в той же строке, и записываем его в столбец 5.Затем это значение, умножая его всякий раз на число из столбца 4, заносим в столбцы 6, 7 и 8. Эти операции проделываем для всех строк таблицы. После того, как все строки таблицы будут заполнены, вычисляем остальные числовые характеристики данного вариационного ряда.

Для определения дисперсии и среднего квадратического отклонения ипользуем формулы (2) и (3):

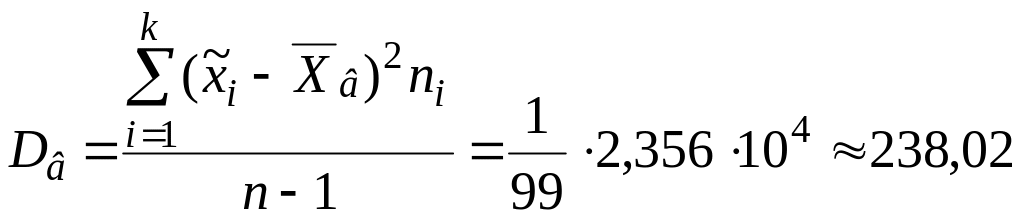
Определим коэффициент вариации:

следовательно, изменчивость роста студентов является незначительной.

Найдем показатели мер косости и крутости, вычислив коэффициенты асимметрии и эксцесса по формулам (5) и (6):

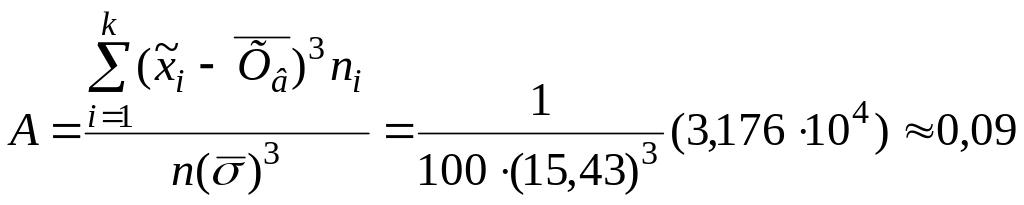
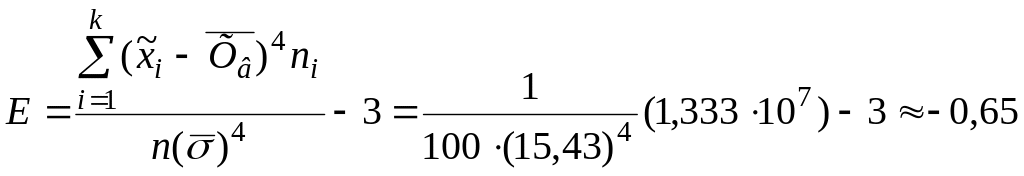
Так как А>0, то асимметрия – левосторонняя. Эксцесс Е<0, следовательно, линия распределения вариант данного ряда проходит ниже кривой нормального распределения.

5. Вычисление ошибок среднего выборочного значения, среднего квадратичного отклонения, коэффициентов вариации, асимметрии, и эксцесса производится с использованием формул (7) – (11).

см

см

Кроме абсолютной ошибки выборочной средней определим и ее относительную ошибку (12):

Следовательно, если утверждать, что генеральная средняя равна полученной выборочной средней, то ошибка при этом составит примерно 0,92%.

Оценка достоверности показателей производится путем вычисления отношения величины рассматриваемого показателя к его ошибке:

Сравниваем полученные показатели достоверности со стандартной величиной t(k, ), при числе степеней свободы k=n–1=100 –1=99 и уровне значимости (Приложение 1). Так как значения показателей достоверности для выборочной средней, среднего квадратичного отклонения и коэффициента вариации больше, чем , то перечисленные статистические показатели достоверны на 5%-ном уровне значимости. Значения показателей достоверности для асимметрии и эксцесса оказываются меньше, чем критическое значение критерия Стьюдента, следовательно, асимметрия и эксцесс недостоверны на 5%–ном уровне значимости, и можно считать, что косость и крутость у эмпирической кривой распределения практически отсутствуют, то есть и .

6. При заданном уровне значимости проверим по критерию Пирсона гипотезу о нормальном распределении генеральной совокупности. Для этого необходимо найти теоретические частоты :

(24)

где n - объем выборки; - длина интервала; - выборочной среднее квадратическое отклонение;

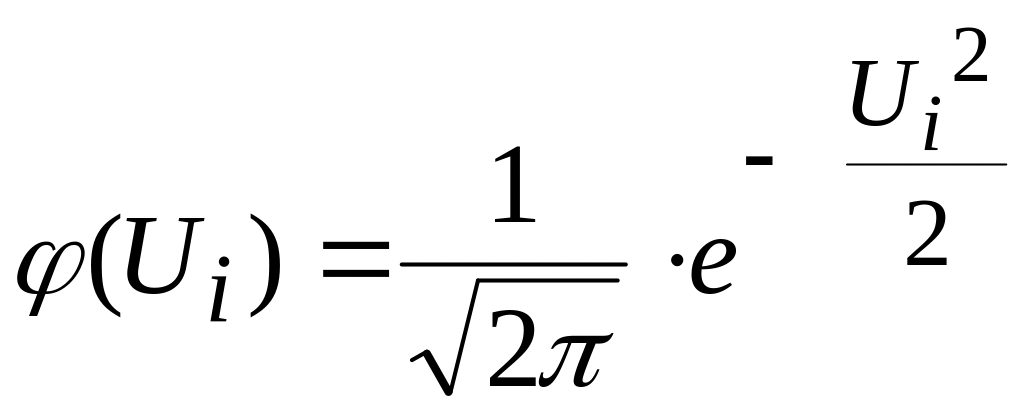(25)

(26)

- середины интервалов (i=1,2, … 8); - выборочное среднее.

Значения функции можно найти по таблице приложения 4.

В данной задаче n=100, =9, =168,3 см, =15,43 см. Тогда, используя формулу (24) имеем:

Определим , а по таблице приложения 4 соответствующее значение . Все необходимые вычисления сведем в таблицу 7.

Таблица 7 – Расчет теоретических частот

i
1	136,5	–31,77	-2,06	0,0478	2,79
2	145,5	–22,77	-1,48	0,1334	7,83
3	154,5	–13,77	-0,89	0,2685	15,63
4	163,5	–4,77	-0,31	0,3802	22,19
5	172,5	4,23	0,27	0,3847	22,41
6	181,5	13,23	0,86	0,2756	16,11
7	190,5	22,23	1,44	0,1415	8,24
8	199,5	31,23	2,02	0,0519	3

Сравним эмпирические ( ) и теоретические ( ) частоты с помощью критерия Пирсона:

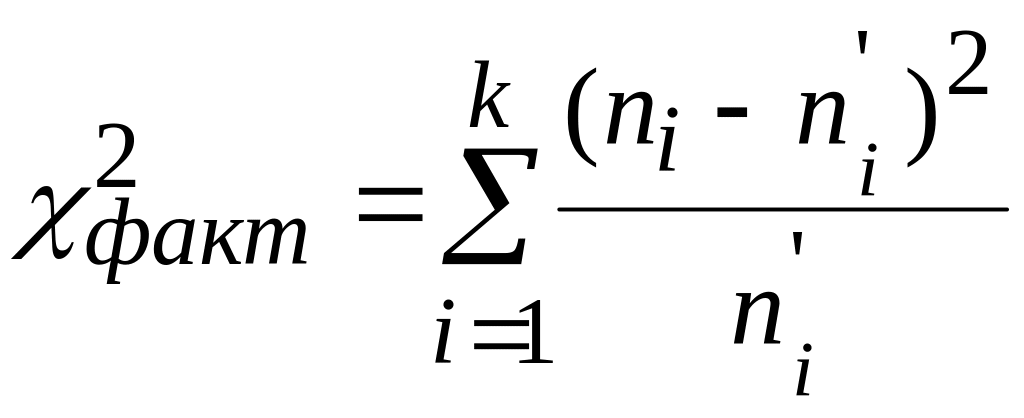(27)

Необходимые вычисления сведем в таблицу 8.

Таблица 8 – Расчет критерия Пирсона

i
1	3	2,79	0,21	0,0441	0,0158
2	9	7,83	1,17	1,3689	0,1748
3	17	15,63	1,37	1,8769	0,1201
4	22	22,19	-0,19	0,0361	0,0016
5	19	22,41	-3,41	11,63	0,5189
6	17	16,11	0,89	0,7921	0,0492
7	8	8,24	-0,24	0,0576	0,0070
8	5	3	2	4	1,3333
	100	98,2

По таблице критических точек распределения (Приложение 3) с заданным уровнем значимости и числу степеней свободы находим критическую точку правосторонней критической области

Так как , то нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности. Таким образом, рост студентов распределен по нормальному закону, и мы можем записать теоретическую плотность распределения этого закона (14) , для которой

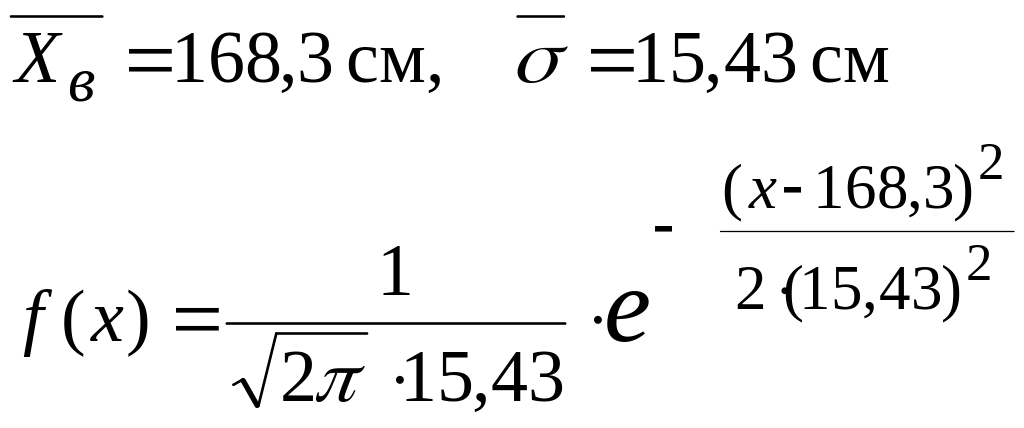
Построим график этой функции – кривую распределения – для точек, абсциссами которых служат - середины выбранных интервалов (i=1,2,...,8), а ординатами – . Вычисление значений можно упростить:

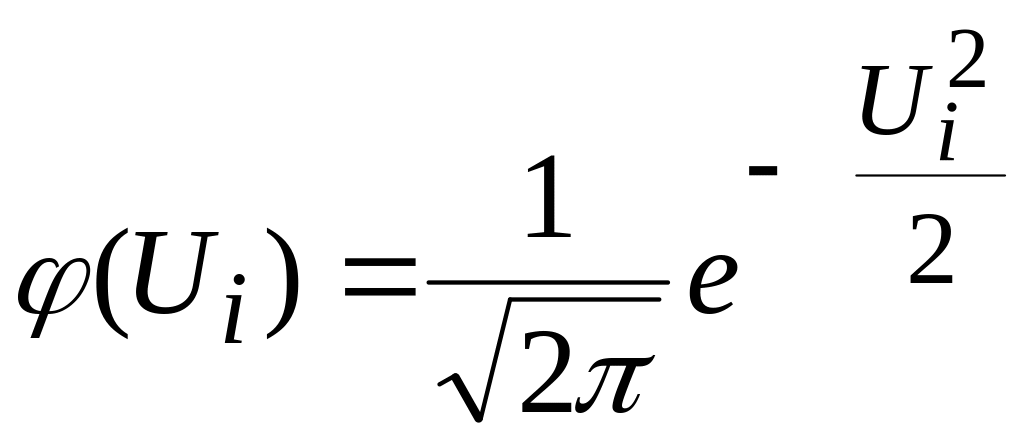где а определяется по таблице приложения 4. При этом можно воспользоваться аналогичными данными из таблицы 7. Все необходимые вычисления сведем в таблицу 9.

Таблица 9 – Расчет значений плотности нормального закона распределения

i
1	136,5	-2,06	0,0478	0,0031
2	145,5	-1,48	0,1334	0,0086
3	154,5	-0,89	0,2685	0,017
4	163,5	-0,31	0,3802	0,025
5	172,5	0,27	0,3847	0,026
6	181,5	0,86	0,2756	0,019
7	190,5	1,44	0,1415	0,011
8	199,5	2,02	0,0519	0,0043

Кроме точек, полученных в таблице 9, построим точку, соответствующую максимуму плотности распределения ) и точки, соответствующие точками перегиба: ). В нашей задаче имеем соответственно: (168,27; 0,03) и (183,52; 0,016), (153,02; 0,016).

Строим теоретическую кривую распределения на рисунке 1 (сплошная линия).

7. Вычислим доверительный интервал для средней в генеральной совокупности по формуле (18), причем

По таблице приложения 1 находим , тогда получаем:

или

Аналогично определяем доверительный интервал для коэффициента вариации в генеральной совокупности, используя формулу (19):

или .

Определим доверительный интервал для среднего квадратического отклонения в генеральной совокупности по формуле (20). По таблице приложения 2 находим значение Тогда имеем:

или

8. Для проведения анализа запишем кратко полученные результаты в следующей последовательности:

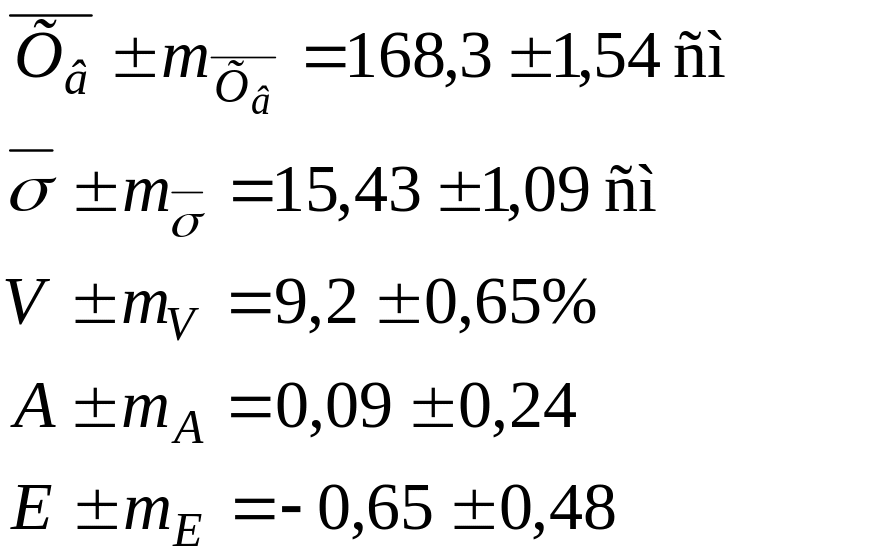
На основании этих результатов можно сделать следующие выводы:

– выборочная средняя роста студентов составляет 168,3 см, а генеральная средняя роста находится в интервале от 165,2 см до 171,3 см.

– изменчивость роста студентов характеризуется средним квадратическим отклонением, которое для выборочной совокупности составляет см, коэффициент вариации равен , что говорит о незначительной изменчивости роста и подтверждается опытными данными. В генеральной совокупности среднее квадратическое отклонение находится в интервале от 13,2 до 17,6 см, а коэффициент вариации – находится в интервале от 7,9% до 10,5 %;

– оценка достоверности основных статистических показателей приводит к выводу о надежности выборочной средней, среднего квадратического отклонения и коэффициента вариации на 5%-ном уровне значимости. В то же время такие показатели как асимметрия и эксцесс, характеризующие меры косости и крутости эмпирической кривой, недостоверны, что позволяет считать их практически отсутствующими;

– на основании проверки критерия согласия Пирсона мы приходим к выводу о том, что рост выбранных студентов можно считать распределенным по нормальному закону с плотностью распределения