1.4 Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона (критерию χ2)

Если по виду гистограммы, а также на основании теоретических предпосылок и анализа опытных данных мы придем к выводу, что изучаемый признак распределен по нормальному закону с плотностью:

f(x)=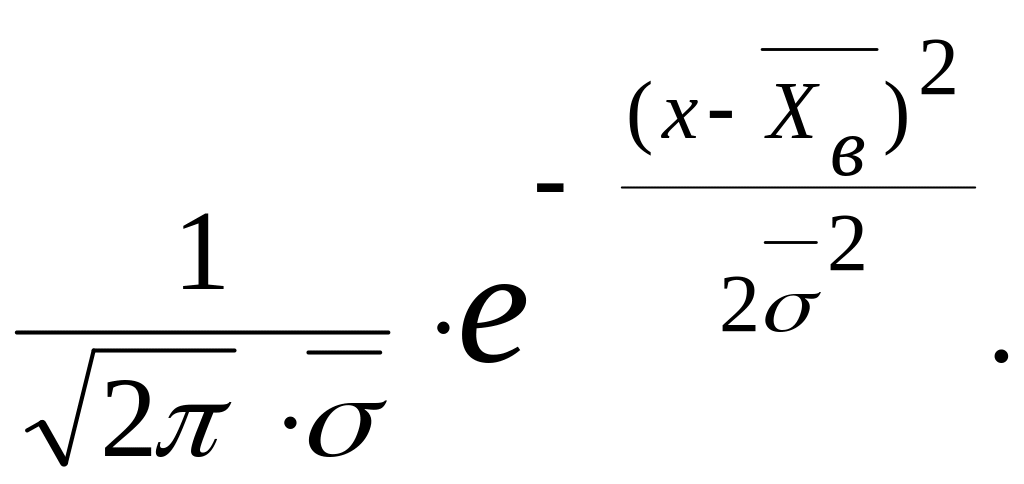 (14)

где – оценка среднего квадратического отклонения, – оценка математического ожидания, то выдвинутую гипотезу о нормальном распределении генеральной совокупности необходимо проверить, применив один из так называемых критериев согласия.

Критерии согласия являются объективными оценками близости фактических распределений к теоретическим. Они позволяют ответить на вопрос, вызвано ли расхождение фактического и теоретического распределения случайными величинами, связанными с недостаточным числом наблюдений, или существенными причинами, то есть тем, что теоретическое распределение плохо воспроизводит фактическое.

Рассмотрим один из критериев согласия – критерий , выведенный Пирсоном (английский математик 1857-1936). В нем за меру отличия эмпирической функции распределения от теоретической принимают величину

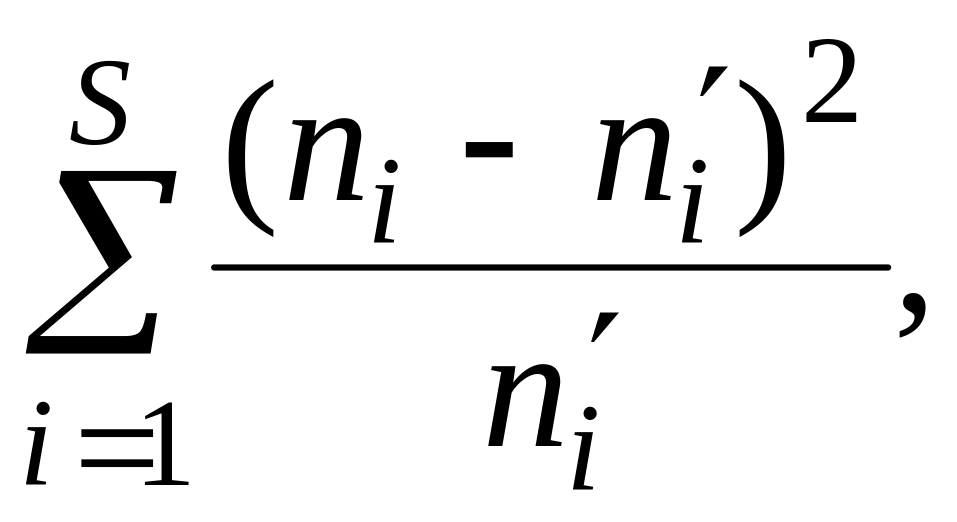= (15)

где - эмпирические частоты, - теоретические частоты, s - число интервалов выборки.

Величина является случайной и имеет, как можно показать, –распределение. В выражении плотности вероятности этого закона распределения параметр назван числом степеней свободы, при этом

(16)

где s – число интервалов выборки, - число параметров теоретического закона.

Так как нормальное распределение определяется двумя параметрами: математическим ожиданием и средним квадратическим отклонением, которые оценивались по выборке, то m = 2 и, следовательно,

(17)

При статистической проверке гипотезы задают уровень значимости , который представляет собой вероятность допустить ошибку первого рода, то есть отвергнуть правильную гипотезу. Чем меньше уровень значимости, тем меньше указанная вероятность. Обычно уровень значимости принимают равным 0,05 или 0,01. Затем, по соответствующим математико-статистическим таблицам (приложение 3) при заданном числе степеней свободы и уровне значимости находим критическую точку Гипотеза не отвергается, если , и отвергается, если > .

1.5 Определение доверительных интервалов среднего значения, среднего квадратического отклонения и коэффициента вариации в генеральной совокупности

Статистические показатели выборочной совокупности являются приближенными оценками неизвестных параметров генеральной совокупности. Оценка может быть представлена одним числом, точкой (точечная оценка) или некоторым интервалом (интервальная оценка), в котором с определенной вероятностью может находиться искомый параметр. Так, выборочная средняя является несмещенной и наиболее эффективной точечной оценкой генеральной средней , а выборочная дисперсия – несмещенной точечной оценкой генеральной дисперсии . Зная ошибку выборочной средней , точечную оценку генеральной средней можно записать в виде . Это означает, что – оценка генеральной средней с ошибкой, равной .

Интервальной называют оценку, которая характеризуется двумя числами – концами интервала, покрывающего оцениваемый параметр. Доверительным называют такой интервал, который с заданной вероятностью покрывает оцениваемый параметр. Центр такого интервала – выборочная точечная оценка, а пределы интервала или доверительные границы определяются средней ошибкой оценки и уровнем доверительной вероятности. Таким образом, интервальная оценка является дальнейшим развитием точечной оценки, которая при малом объеме выборки неэффективна. В общем виде, доверительный интервал для генеральной средней записывают так:

(18)

где – генеральная средняя, – выборочная средняя, – ошибка выборочной средней, – значение критерия Стьюдента, где – число степеней свободы, – уровень значимости, , – доверительная вероятность или надежность.

Аналогично строится доверительный интервал для коэффициента вариации в генеральной совокупности:

(19)

где – коэффициент вариации генеральной совокупности, – коэффициент вариации выборочной совокупности, – ошибка коэффициента вариации, – значение критерия Стьюдента.

Для нахождения доверительного интервала для среднего квадратического отклонения в генеральной совокупности по найденному выборочному значению используем формулу:

(20)

Для определения необходимо воспользоваться таблицей (Приложение 2).