Методи обчислення середніх у рядах динаміки
В окремих випадках виникає потреба у визначенні середньої величини з рівнів ряду динаміки.
При визначені середнього рівня або інтервального ряду враховуються відмінності між ними.
Середній рівень інтервального (періодичного) ряду динаміки з рівними інтервалами часу визначають за формулою середньою арифметичною простою.
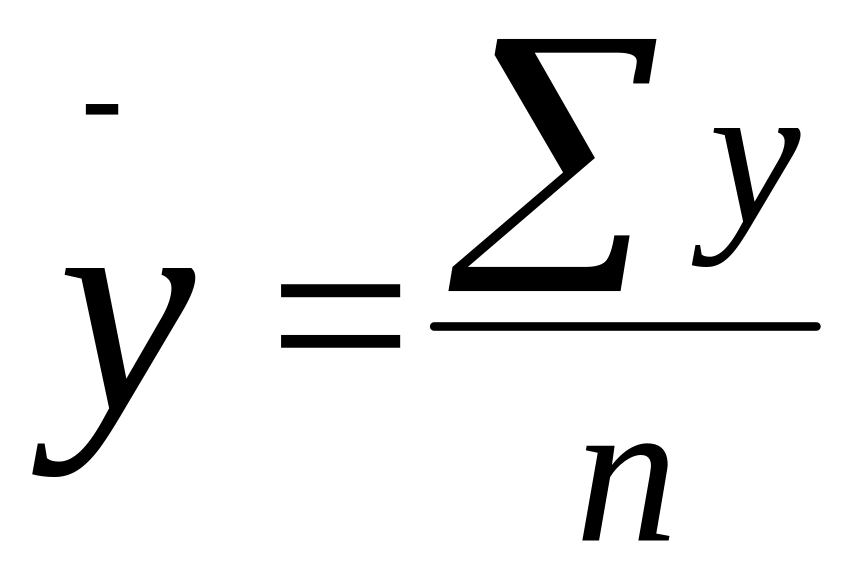де
y - середній рівень ряду; n – число рівнів
ряду динаміки.
Приклад
Випуск студентів денного відділення ХФЭК (людина)
1997 |
1998 |
1999 |
2000 |
2001 |
2002 |
102 |
100 |
110 |
130 |
140 |
150 |
Середній рівень моментного ряду динаміки з рівними проміжками часу між датами визначають за формулою середньої хронологічної:
,
Приклад
На 1 січня |
На 1 лютого |
На1 березня |
На 1 квітня |
На 1 травня |
На 1 червня |
На 1 липня |
200 |
150 |
130 |
190 |
210 |
230 |
210 |
У моментно му ряді динаміки з нерівними проміжками між датами середній рівень визначають за формулою середньої арифметичної зваженої
,
де у - середній рівень ряду;
t – тривалість періоду між окремими датами.
Приклад
Залишки продукції на складі підприємства характеризується наступними даними, (тис.грн). Знайти середньорічні залишки продукції на складі/
01.01.2002 |
01.03.2002 |
01.07.2002 |
01.08.2002 |
254 |
260 |
268 |
268 |
З 1 січня до 1 березня – два місяці, з 1 березня до 1 липня чотири місяці,
з 1 липня до 1 серпня – один місяць, з 1 серпня до 1 січня наступного року – 5 місяців.
Визначаємо середньорічні залишки продукції на складі:
\
Відомі наступні дані про розмір торговельних площ магазинів фірми (на кінець року):
Роки |
2006 |
2007 |
2008 |
2009 |
Торговельна площа, м2 |
4 191 |
4 316 |
4 431 |
4 541 |
Визначте основні аналітичні показники ряду динаміки.
Розв’язок:
Визначимо середній рівень динамічного ряду. Ряд моментний, тому середній рівень знаходимо за середньою хронологічною:
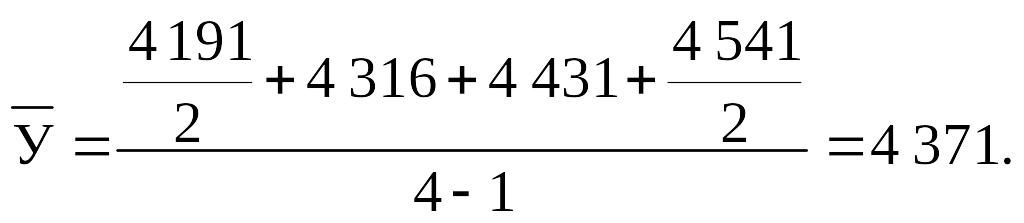
Визначимо абсолютні відхилення:
а) ланцюгові б) базисні
4 316 – 4 191 = +125 4 316 – 4 191 = +125
4 431 – 4 316 = +115 4 431 – 4 191 = +240
4 541 – 4 431 = +110 4 541 – 4 191 = +350
Впевнимося, що сума ланцюгових відхилень дає останнє базисне:
+ 125 + 115 + 110 = 350.
Визначимо темпи зростання (у процентах):
а) ланцюгові б) базисні
Впевнимося, що добуток ланцюгових темпів зростання, взятих в разах, дає останній базисний темп
Визначимо темпи приросту (у процентах):
а) ланцюгові б) базисні
103,0 – 100 = + 3,0 103,0 – 100 = + 3,0
102,7 – 100 = + 2,7 105,7 – 100 = + 5,7
102,5 – 100 = + 2,5 108,4 – 100 = + 8,4
Зв’язку між темпами приросту немає.
Визначимо абсолютне значення одного процента щорічного приросту:
Приведені розрахунки оформлюють в таблиці:
Роки |
Вихідний рівень ряду динаміки (торгова площа, м2) |
Абсолютні відхилення (±) |
Темпи зростання, % |
Темпи приросту, (зменшення) (±), % |
Абсолютне значення 1 % приросту |
|||
ланцюгові
|
базисні
|
ланцюгові Тл |
базисні Тб |
ланцюгові
|
базисні
|
|||
2006 |
4 191 |
– |
– |
– |
100,0 |
– |
– |
– |
2007 |
4 316 |
+125 |
+125 |
103,0 |
103,0 |
+3,0 |
+3,0 |
41,7 |
2008 |
4 431 |
+115 |
+240 |
102,7 |
105,7 |
+2,7 |
+5,7 |
42,6 |
2009 |
4 541 |
+110 |
+350 |
102,5 |
108,4 |
+2,5 |
+8,4 |
44,0 |
Визначаємо середнє ланцюгове (щорічне) абсолютне відхилення:
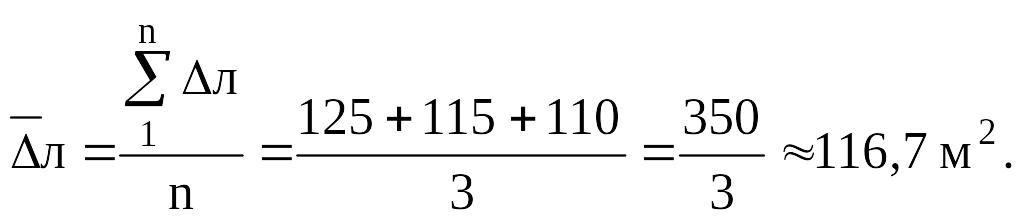
Визначаємо середній ланцюговий (щорічний) темп зростання:
або 
Визначаємо середній ланцюговий темп приросту (за загальним правилом):
Таким чином, щорічно торговельні площі зростали у даної фірми в середньому на 2,7%.
Темпи зростання із року в рік уповільнювалися, про це свідчать значення коефіцієнтів прискорення (уповільнення), які менші від 1.