Теорема (про структуру загального розв’язку лодр)

Якщо функції та є розв’язками рівняння (*), то функція також буде розв’язком ЛОДР при умові, що та - лінійно незалежні, тобто .

- загальний розв’язок ЛОДР.

Ейлер запропонував шукати частинні розв’язки цього рівняння у вигляді , де k – стала (дійсна чи комплексна), яку треба знайти.

,

,

, тоді - характеристичне рівняння

лінійного однорідного диференціального рівняння другого порядку.

Позначимо корені характеристичного рівняння через k₁ і k₂ .

Формули для загального розв’язку лодр

1) Якщо k₁ k₂ (дійсні, різні числа) (дискримінант D>0), то

2) Якщо k₁=k₂ (дійсні, рівні числа)

(

D=0), то

3) Якщо k_{1, 2} = (комплексно - спряжені числа) (D<0), то

Приклади: Знайти загальний розв’язок:

1)

складаємо характеристичне рівняння

2)

Розглянемо розв’язки лінійного неоднорідного диференціального рівняння другого порядку із сталими коефіцієнтами

.

Теорема (про структуру загального розв’язку лндр)

Загальний розв’язок ЛНДР являє собою суму загального розв’язку відповідного однорідного рівняння і довільного частинного розв’язку даного рівняння.

, де у₀ – загальний розв’язок відповідного ЛОДР,

у_* - частинний розв’язок ЛНДР.

Є рівняння із спеціальною правою частиною, для яких знайдені частинні розв’язки.

1) , де - многочлен (поліном) степеня n.

, де

- многочлен (поліном) степеня n з невідомими коефіцієнтами;

r знаходимо з умови:

1. r=0, якщо (k₁ і k₂ – корені характеристичного рівняння).

2. r=1, якщо k₁ =0 (або k₂ =0).

Приклад: Знайти загальний розв’язок рівняння: .

у₀ - ?

у_* - ?

=

так як k₁ = 0, то r = 1

Потрібно знайти А, В, С:

Підставимо в дане рівняння:

Застосуємо метод невизначених коефіцієнтів:

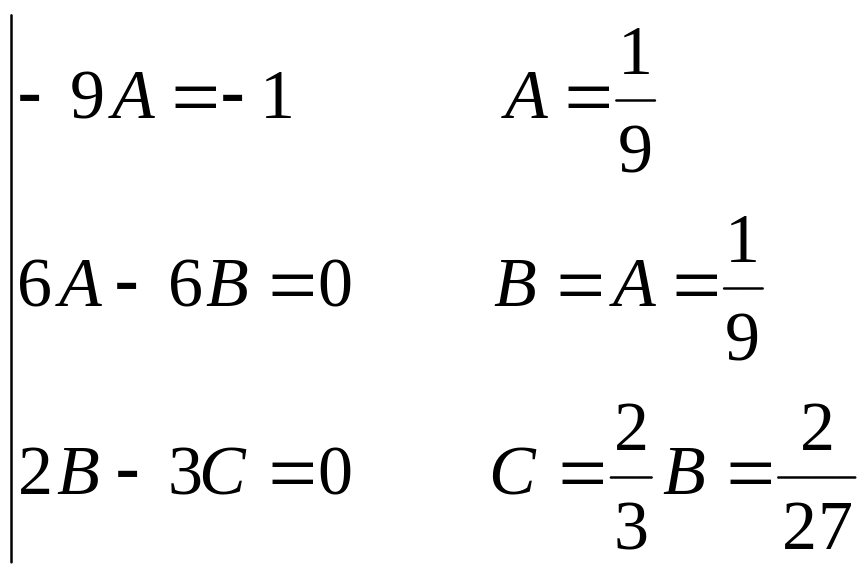
- загальний розв’язок рівняння.

2) , де М і - сталі числа.

, де А – невідоме число;

r знаходимо з умови:

1. r = 0, якщо

2. r = 1, якщо (або )

3. r = 2, якщо

Приклад:

у₀ - ?

у_* - ?

так як , то r = 1

Підставимо в дане рівняння:

,

,

,

- загальний розв’язок

3) , де M і N – сталі числа.

, де А і В – невідомі числа;

r знаходимо з умови:

1. r = 0, якщо

2. r = 1, якщо

Приклад:

у₀ - ?

Підставимо в дане рівняння:

;

;

- загальний розв’язок

Завдання додому

1) Конспект; [1] с. 470 – 493;

[2] с. 340 – 350.

Питання для самоконтролю

1. Лінійні диференціальні рівняння другого порядку.

2. Однорідні та неоднорідні рівняння.

Л Е К Ц І Я 30

Тема: Лінійні різницеві рівняння із сталими коефіцієнтами.

Мета: сформувати поняття різницевого рівняння порядку k; ознайомити з методами розв’язування різницевих рівнянь, застосуванням різницевих рівнянь в економіці.

Література: 1, с. 478-483; 6, с. 441-444].

П Л А Н

1. Однорідні лінійні різницеві рівняння.

2. Неоднорідні лінійні різницеві рівняння.

1. Означення. Нехай у₀, у₁, у₂, у₃, ... – послідовність дійсних чисел. Різницевим рівнянням порядку k називають рівняння, що зв’язує у₀, у₁, у₂, у₃, ..., у_n+k для кожного значення n = 0, 1, 2, 3 ...

Приклад: Визначити порядок різницевих рівнянь:

а) - 3-го порядку

б) - 2-го порядку

в) + - 1-го порядку

Розв’язком різницевого рівняння називають таку множину значень , яка задовольняє різницеве рівняння для усіх можливих значень n.

Однорідним різницевим рівнянням 1-го порядку називають рівняння виду або .

Теорема: Загальним розв’язком різницевого рівняння вигляду , де - задана стала, буде , де С – довільна стала

Доведення. В дане рівняння підставимо значення n = 1, 2, 3, ... Одержимо:

n = 1

n = 2

n = 3

n = 4

...

Порівнюючи з формулою бачимо, що , що й потрібно було довести.

Щоб знайти частинний розв’язок різницевого рівняння, потрібно задати початкові умови.

Зауваження: Якщо , то розв’язок зростає за показниковим законом; якщо - спадає.

Приклад: Знайти частинний розв’язок рівняння при початкових умовах

Запишемо формулу ,

.

Використовуючи початкові умови знайдемо С: при n = 5

Неоднорідним різницевим рівнянням 1-го порядку називається рівняння виду

.