Контрольная работа № 1 (Менеджмент, финансы, экономика)

Задание 1 (для всех вариантов).

Известны координаты четырех вершин пирамиды ABCD: A, B, C, D.

Нужно найти: 1) длину АВ; 2) угол между АВ и ВС; 3) площадь треугольника АВС; 4) объем пирамиды; 5) длину высоты DH пирамиды (проведенной к плоскости АВС).

Нужно составить уравнения: 6) прямой АВ; 7) плоскости АВС;

8) высоты DH, проведенной из D перпендикулярно к плоскости АВС;

8. 9) медианы АМ треугольника АВС; 10) высоты АК треугольника АВС;

11) биссектрисы AL треугольника АВС.

Вариант 11.

1. А (1, -2, 3), В (1, 10, 8), С (1, 4, 0), D (2, -2, 2).

2. Составить уравнение прямой линии, которая проходит через точку М (-1; 7; 2) параллельно к линии пересечения плоскостей x + y + 4z = 0 и YOZ.

3. Найти f (A), если f (x) = -x² + x - 5, A=

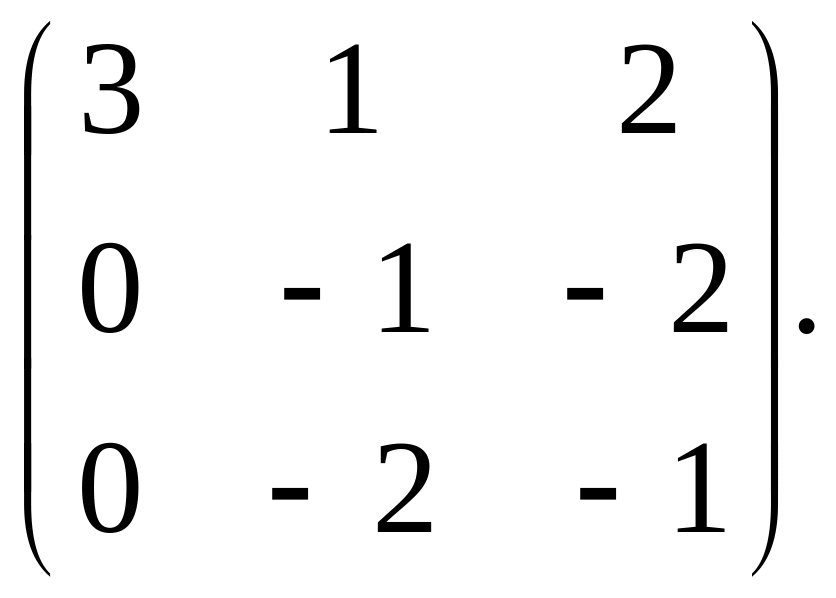
4. Решить систему уравнений матричным методом:

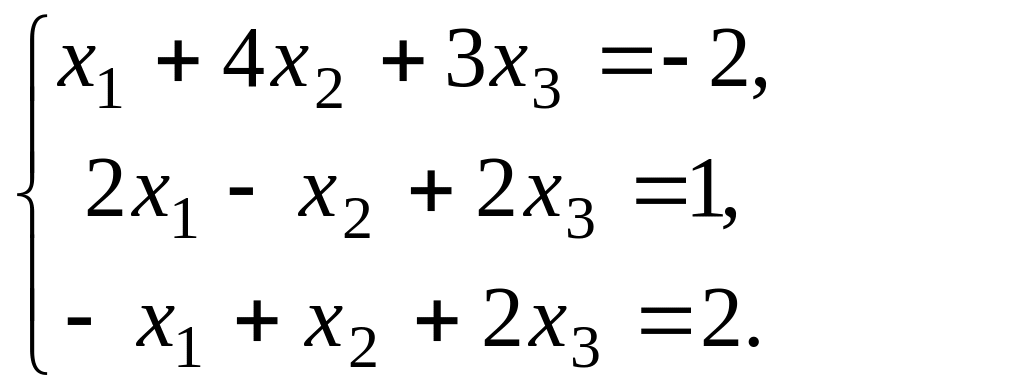
5. Привести уравнение кривой к каноническому виду, изобразить кривую и все системы координат: 11x² - 56xy - 22y² + 40x + 25 = 0.

6. Найти пределы:

1) ; 2) ; 3) .

7. Найти производную данной функции и значение производной в заданной точке: , x =/2.

8.Найти уравнение касательной к кривой в точке М, получаемой при t = t₀:

, , t₀ = /3.

9.

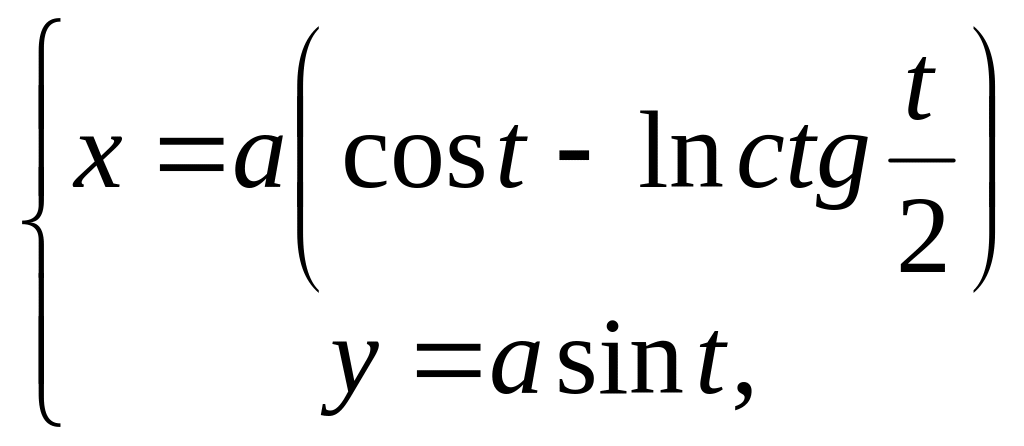
10. Найти пределы по правилу Лопиталя: ;

11. Выполнить полное исследование функций и построить их графики:

1) y = (2- x²)/ ; 2) y = ;

Перейдя к полярной системе координат, построить график:

(x² + y² )³ = 27x²y².

Контрольная работа № 1 (Менеджмент, финансы, экономика)

Задание 1 (для всех вариантов).

Известны координаты четырех вершин пирамиды ABCD: A, B, C, D.

Нужно найти: 1) длину АВ; 2) угол между АВ и ВС; 3) площадь треугольника АВС; 4) объем пирамиды; 5) длину высоты DH пирамиды (проведенной к плоскости АВС).

Нужно составить уравнения: 6) прямой АВ; 7) плоскости АВС;

8) высоты DH, проведенной из D перпендикулярно к плоскости АВС;

8. 9) медианы АМ треугольника АВС; 10) высоты АК треугольника АВС;

11) биссектрисы AL треугольника АВС.

Вариант 12.

1. А (1, -3, 2), В (1, 2, 14), С (1, 3, 0), D (-1, 3, -2).

2. Проверить, что точки А (-1; 3; 4), В (0; 1; 5), С (-2; 3; 5) и D (6; 0; 0) принадлежат одной плоскости, и составить уравнение этой плоскости.

3. Найти f (A), если f (x) = -2x² - 3x + 5, A=

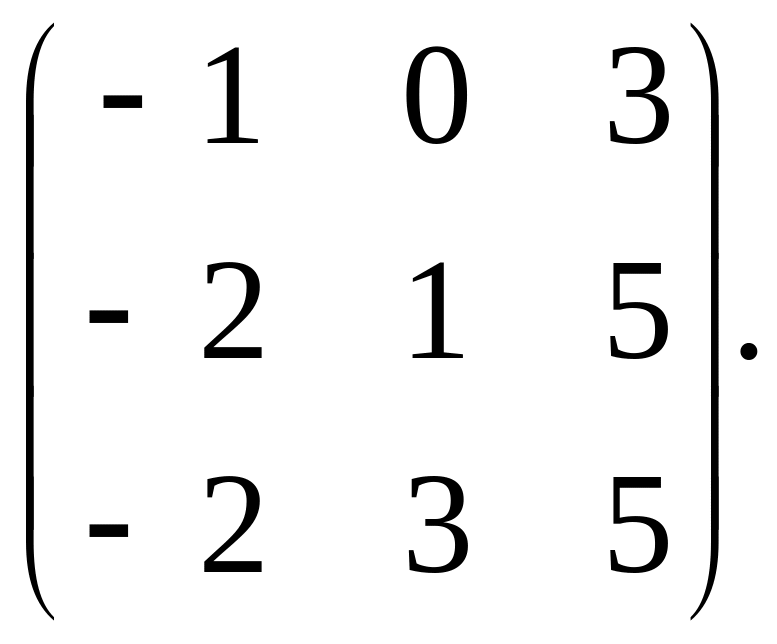
4. Решить систему уравнений матричным методом:

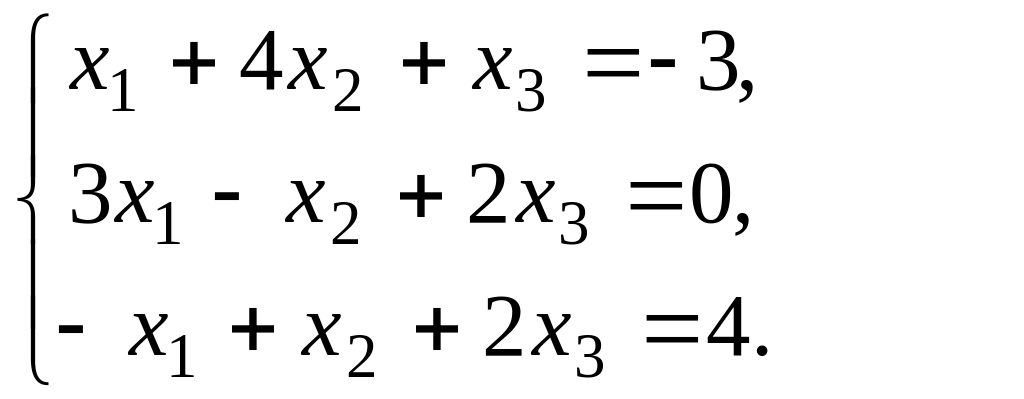
5. Привести уравнение кривой к каноническому виду, изобразить кривую и все системы координат: 60x² + 28xy + 15y² + 225y + 32 = 0.

6. Найти пределы:

1) ; 2) ; 3) .

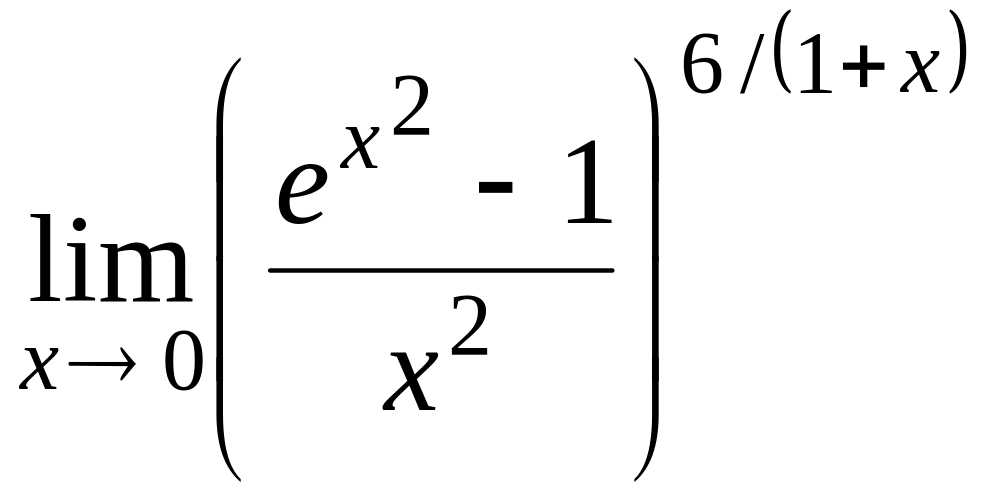7. Найти производную данной функции и значение производной в заданной точке: , x = 1.

8.Найти уравнение касательной к кривой в точке М, получаемой при t = t₀:

, , t₀ = 1.

9. Доказать, что функция y = y(x), заданная параметрически: ; , является решением уравнения .

10. Найти пределы по правилу Лопиталя: ;

11. Выполнить полное исследование функций и построить их графики:

1. y = (4x³ – 3x)/(4x² - 1); 2) y = ;

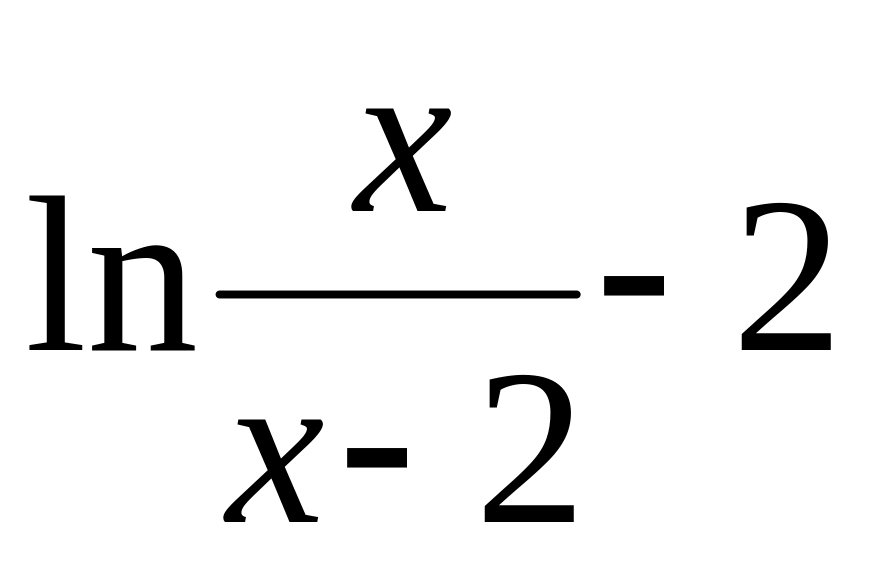Перейдя к полярной системе координат, построить график:

(x² + y²)² = 4x² + y².