Тема1: Однофакторные регрессионные модели и метод их построения

Задание 1. По данным таблицы 1. построить линейное уравнение регрессии, отражающее зависимость стоимости квартиры от ее жилой площади

Таблица 1

№ п.п	Стоимость, тыс.руб.	Площадь, м2	№ п.п	Стоимость, тыс.руб.	Площадь, м2
1	780	42	17	900	32
2	1000	44	18	2900	80
3	1100	30	19	3000	80
4	1200	34	20	2500	76
5	1600	40	21	4000	120
6	1500	43	22	1200	35
7	1800	50	23	1600	36
8	2000	60	24	1800	40
9	1850	56	25	1900	56
10	2100	64	26	1700	56
11	1300	36	27	1800	62
12	1600	56	28	1800	60
13	1700	56	29	1850	64
14	1800	60	30	1550	45
15	1750	58	31	1600	56
16	1850	65	32	1800	64

Для построенного уравнения вычислить

1) коэффициент корреляции;

2) коэффициент детерминации;

3) дисперсионное отношение Фишера;

4) стандартные ошибки коэффициентов регрессии;

5) t-статистики Стьюдента;

6) доверительные границы коэффициентов регрессии

Дать содержательную интерпретацию коэффициента регрессии построенной модели. Все расчеты провести в Excel с использованием выше приведенных формул.

Задание 2. По данным табл. 1 построить нелинейное уравнение регрессии в виде показательной функции, отражающее зависимость стоимости квартиры от ее полезной площади. Для построенного уравнения вычислить:

1) индекс корреляции;

2) Коэффициент детерминации;

3) Дисперсионное отношение Фишера.

Дать содержательную интерпретацию коэффициента регрессии построенной модели. Все расчеты провести в Excel с использованием выше приведенных формул.

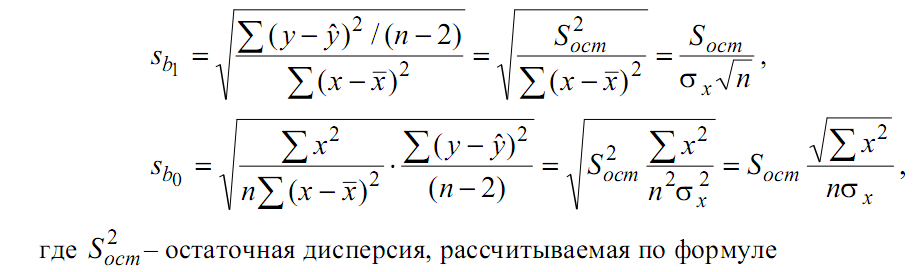
Пример решения

Решение с помощью табличного процессора Excel

1. Ввод исходных данных.

2. Подготовка данных и оформление их в виде табл. 2 для расчета оценок коэффициентов регрессии.

Таблица 2

№ п.п.	у	x	x2	ху	y2
1.	5000	30.2	912.04	151000	25000000
2.	5200	32	1024	166400	27040000
3.	5350	32	1024	171200	28622500
4.	5880	37	1369	217560	34574400
5.	5430	30	900	162900	29484900
6.	5430	30	900	162900	29484900
7.	5430	30	900	162900	29484900
8.	5350	29	841	155150	28622500
9.	5740	33	1089	189420	32947600
10.	5570	31	961	172670	31024900
11.	5530	30	900	165900	30580900
12.	6020	34	1156	204680	36240400
13.	7010	38	1444	266380	49140100
14.	6420	31	961	199020	41216400
15.	7150	39	1521	278850	51122500
16.	7190	39.5	1560.3	284005	51696100
Среднее значение	5856.25	32.86	1091.39	194433.44	34767688.50

данными таблицы 3

8. Построение линейного уравнения регрессии и расчет всех его характеристик с помощью «Пакета анализа» табличного процессора Excel. Сравнение результатов, полученных с помощью расчетных формул, с результатами применения инструментальных средств Excel показывает их полную идентичность, что свидетельствует о правильном понимании метода построения линейных регрессионных уравнении и методики оценки его качества.

Таблица 3

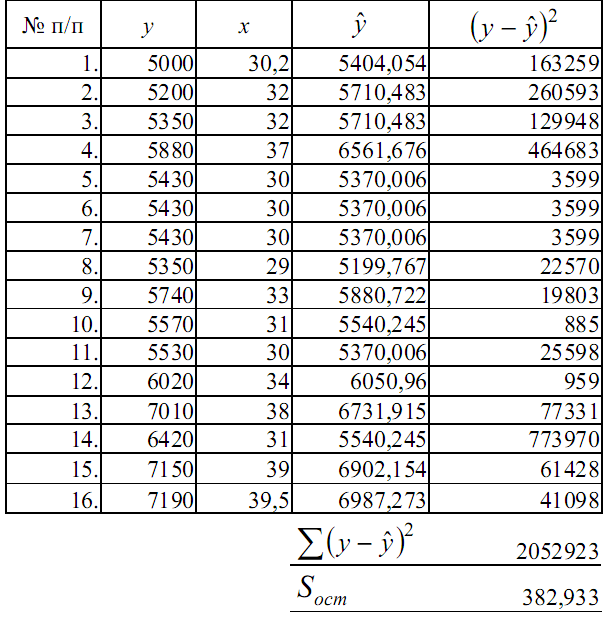
Пример решения

1. Ввод исходных данных.

2. Подготовка данных и оформление их в виде табл. 4 для расчета коэффициентов регрессии.

Таблица 4

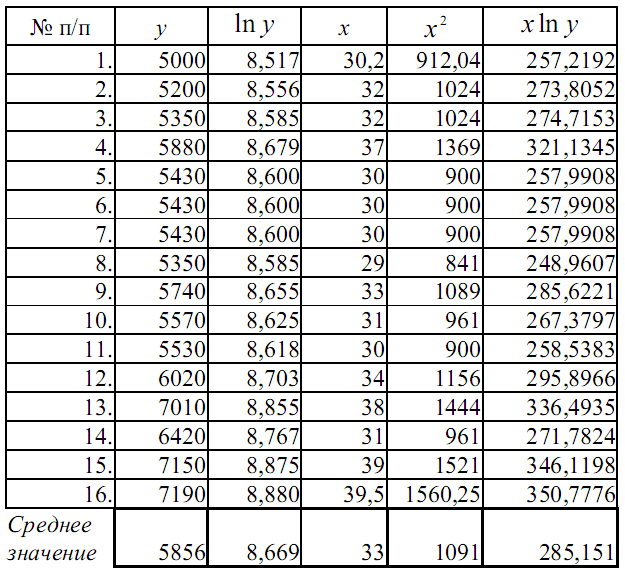
3. Расчет индекса корреляции и коэффициента детерминации с оформлением промежуточных вычислений в виде табл. 5.

Таблица 5

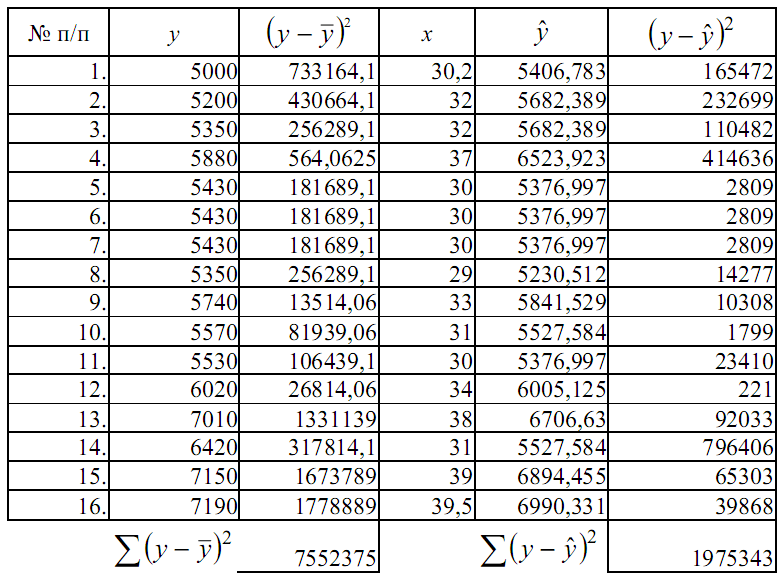
При использовании показательной зависимости изменения стоимости квартиры объясняются соответствующими изменениями полезной площади на 73,84%.

4. Расчет дисперсионного отношения Фишера

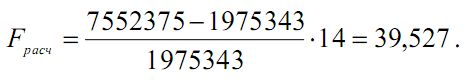
Сравнение расчетного значения t-критерия с табличным F_{1, 14} = 4,60 для 95%-ного уровня значимости позволяет сделать вывод об адекватности по- строенной модели.

5. Построенная регрессионная модель в виде показательной функции

у = 2347,862*1,028^x

позволяет утверждать, что в среднем увеличение полезной площади на 1 кв.м. повышает стоимость квартиры в 1,028 раза.