Способы преобразования чертежа

137. Задание {{ 137 }} ТЗ № 137

На котором чертеже ошибочно определена натуральная величина плоской фигуры способом вращения. Натуральная величина обведена более толстыми (широкими) линиями.

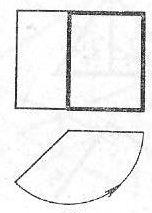
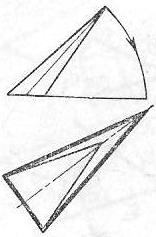
1 2 3 4

 1

 2

 3

 4

138. Задание {{ 138 }} ТЗ № 138

На котором чертеже ошибочно определена натуральная величина треугольника ABC вращением вокруг фронтали или горизонтали.

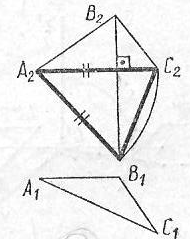
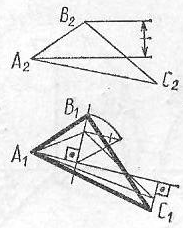
1 2 3 4

 1

 2

 3

 4

139. Задание {{ 139 }} ТЗ № 139

Которую прямую следует переместить в проецирующее положение с тем, чтобы плоскость ABC преобразилась в горизонтально проецирующую.

 CD

 AB

 BC

 AC

140. Задание {{ 140 }} ТЗ № 140

В которой задаче допущена ошибка при определении натуральной величины прямой способом прямоугольного треугольника.

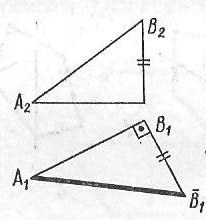
1 2 3 4

 1

 2

 3

 4

141. Задание {{ 141 }} ТЗ № 141

Перпендикулярно к которой прямой следует разместить новую плоскость проекций с тем, чтобы заданная плоскость стала в новой системе проецирующей.

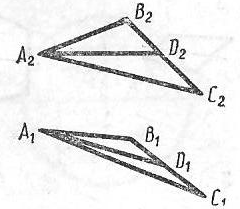
 AB

 AC

 BC

 AD

142. Задание {{ 142 }} ТЗ № 142

Чтобы найти проекцию А₄ точки А в новой плоскости проекций π₄ нужно от А_х отложить отрезок А_хА₄ равный

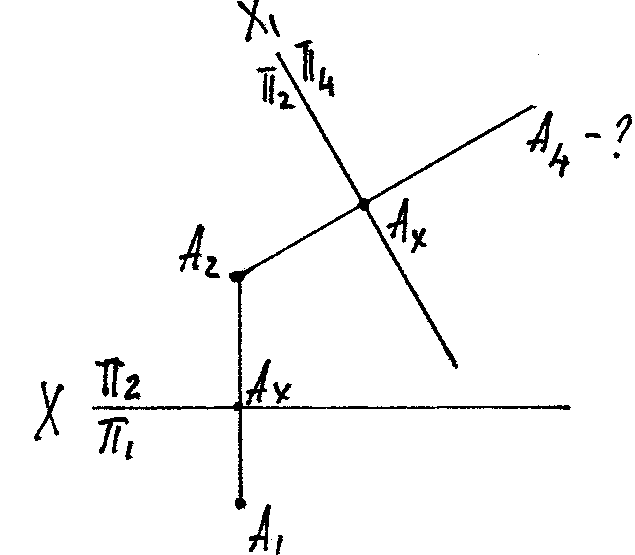
 А₂А_х

 А₁А_х

 А₁А₂

 А₂А_х1

143. Задание {{ 143 }} ТЗ № 143

Будет ли плоскость треугольника АВС проецирующей по отношению к новой плоскости проекции π₄

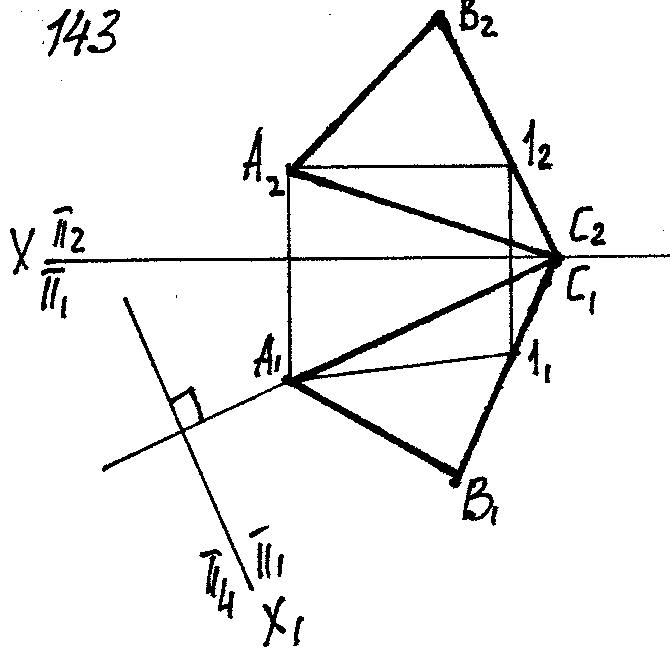
 Да, так как А₁С₁ перпендикулярно Х₁

 Нет. Горизонталь А₁ не перпендикулярна оси Х₁

 Нет, так как ось Х₁ не перпендикулярна оси Х₁

 Нет, так как требуется два преобразования

144. Задание {{ 144 }} ТЗ № 144

Как перемещаются проекции точки при вращении ее вокруг оси, перпендикулярной плоскости π₂

 Горизонтальная – по окружности, фронтальная по прямой, параллельной оси Х

 Горизонтальная - по прямой, параллельной оси Х, фронтальная – по окружности

 Горизонтальная - по прямой, перпендикулярной оси вращения, фронтальная – по дуге эллипса

 Горизонтальная и фронтальная проекции – по прямой, параллельной оси Х

145. Задание {{ 145 }} ТЗ № 145

Как располагаются фронтали плоскости совмещенной с фронтальной плоскостью проекций

 Параллельно совмещенному горизонтальному следу плоскости

 Перпендикулярно совмещенному горизонтальному следу плоскости

 Параллельно первоначальному положению фронтального следа плоскости

 Перпендикулярно первоначальному положению фронтального следа плоскости

146. Задание {{ 146 }} ТЗ № 146

Вокруг какой прямой нужно повернуть плоскость, чтобы она совместилась с горизонтальной плоскостью проекций

 Вокруг оси перпендикулярной плоскости π₁

 Вокруг фронтали плоскости

 Вокруг горизонтального следа плоскости

 Вокруг горизонтали плоскости

147. Задание {{ 147 }} ТЗ № 147

Горизонтали плоскости, совмещенной с плоскостью π₁ располагаются

 Параллельно горизонтальному следу плоскости, т.е. оси вращения

 Параллельно фронтальному следу плоскости

 Параллельно совмещенному фронтальному следу плоскости

 Параллельно оси проекции Х

148. Задание {{ 148 }} ТЗ № 148

Чтобы найти проекцию А₄ точки А в новой плоскости проекции π₄ нужно от А_х1 отложить отрезок равный ….

 А₂А_х

 А_хА₁

 А₂А₁

 А₁А_х1

149. Задание {{ 149 }} ТЗ № 149

Для определения истинного вида плоской фигуры общего положения требуется произвести….

 Две замены плоскости проекции

 Одну замену плоскости проекции

 Три замены плоскости проекции

 Четыре замены плоскости проекции

150. Задание {{ 150 }} ТЗ № 150

Будет ли плоскость треугольника АВС перпендикулярна плоскости π₄

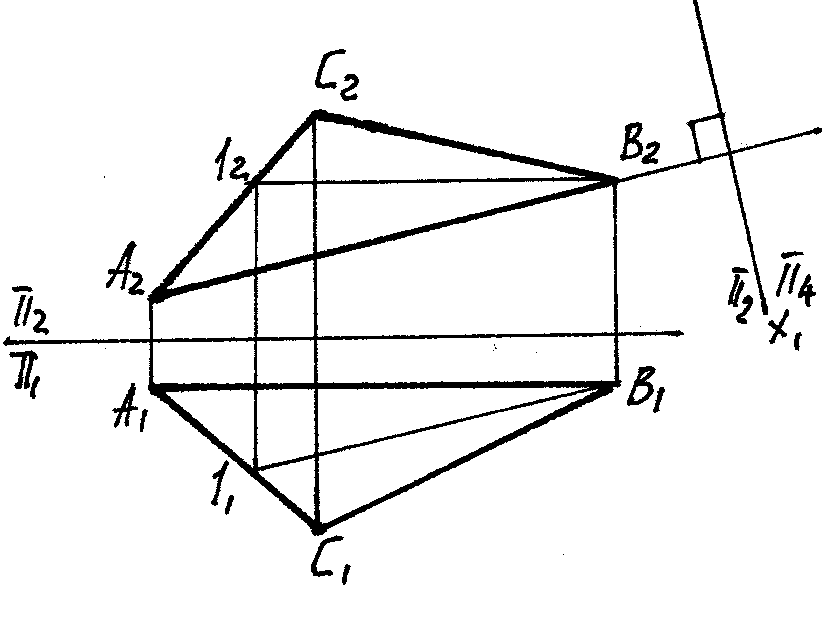
 Нет, так как оси х₄х₁ не перпендикулярны друг другу

 Да, так как ось х₁ перпендикулярна горизонтали АВ

 Нет, так как новая плоскость проекций не перпендикулярна

фронтали 1 В

 Да, так как в плоскости треугольника АВС есть прямая СВ

параллельная π₄

151. Задание {{ 151 }} ТЗ № 151

Как перемещаются проекции точки при вращении ее вокруг оси, перпендикулярной плоскости π₁

 Горизонтальная по дуге окружности, фронтальная – по прямой параллельной оси Х

 Горизонтальная по прямой, параллельной оси Х, фронтальная – по дуге окружности

 Горизонтальная по прямой перпендикулярной оси вращения, фронтальная по произвольной прямой

 Горизонтальная и фронтальная проекции – по прямой, параллельной

оси Х