10

Глава 2 Нумерация формул и рис.!

АТМОСФЕРНОЕ ДАВЛЕНИЕ

2.1. Статика атмосферы

Силы, действующие в атмосфере. Раздел метеорологии, изучающий закономерности строения атмосферы при отсутствии движения ее относительно поверхности Земли называется статикой атмосферы.

Силы, действующие на атмосферу и в атмосфере делятся на массовые и поверхностные.

Массовые силы – сила тяжести и отклоняющая сила вращения Земли (Кориолисова сила). Эти силы действуют на каждую частицу атмосферы.

Поверхностные силы – силы трения и давления.

Сила трения и отклоняющая сила вращения Земли действуют только при движении атмосферы относительно ее поверхности или при движении одних слоев атмосферы относительно других.

Силы тяжести и давления действуют в атмосфере и в состоянии ее по­коя. Рассмотрим эти силы.

Сила тяжести. Любое тело притягивается к Земле с силой , равной произведению его массы т на ускорение свободного давления :

. (2.1)

Эта сила называется силой тяжести. Для объема воздуха с единичной массой сила тяжести равна ускорению свободного падения.

Ускорение свободного падения для каждой частицы атмосферы являет­ся результирующей ускорения гравитационного притяжения и центро­бежного ускорения :

. (2.2)

Центробежная сила возникает в результате суточного вращения Зем­ли и атмосферы. Она направлена перпендикулярно оси вращения Земли.

2.2. Основное уравнение статики

Основное уравнение статики определяет изменение давления с высотой. Для вывода основного уравнения статики рассмотрим неподвижную атмосферу. Выделим объем воздуха с единичными горизонтальными основаниями и рассмотрим силы, действующие на этот объём (см. рис. 2.1).

Рис.2.1. Силы, действующие на единичный объем воздуха

Спроецируем силы, действующие на выделенный объем, на ось z. В результате получим:

p – (р + dp) – Р = 0, (2.4)

где: р – давление воздуха на уровне z,

Р – вес выделенного объема воздуха. Определяется по формуле:

Р = (2.5)

Раскроем скобки и после сокращения одинаковых членов получим:

– dp = Р (2.6)

Подставив выражение (2.5) в (2.6) и произведя преобразования, получим основное уравнение статики:

. (2.8)

Это уравнение физически выражает собой равновесие двух сил –

градиента давления и силы тяжести. Данное выражение является одним из важнейших уравнений метеорологии.

Следствия из основного уравнения статики:

• давление с высотой всегда убывает;

• давление воздуха на любом уровне равно массе столба воздуха единичного сечения высотой от данного уровня до границы атмосферы;

• в закрытых помещениях (но не герметизированных) давление на всех уровнях не отличается от давления в окружающем пространстве;

• при подъеме на одну и ту же высоту падение давления тем больше, чем больше плотность, которая зависит от температуры.

В холодной воздушной массе давление с высотой понижается быстрее. В холодной воздушной массе на высоте преобладает низкое давление.

2.3. Модели атмосферы

Под моделями атмосферы подразумеваются предполагаемые изменения давления с высотой.

Однородная атмосфера – такая атмосфера, в которой плотность воздуха с высотой не изменяется.

Для получения выражения изменения давления с высотой проинтегри­руем основное уравнение статики:

р = р₀ – . (2.14)

В однородной атмосфере давление с высотой изменяется по линейному закону (см. рис. 2.2).

Рис.2.2. Распределение давления с высотой в однородной атмосфере

Подставим в (2.14) значение р равное нулю и получим выражение для определения высоты однородной атмосферы:

. (2.15)

Заменим в (2.15) р₀ правой частью уравнения состояния сухого воздуха (1.2^*) и после сокращения получим:

. (2.16)

Подставим в выражение (2.16) числовые значения: R_с = 287 м²/с²К,

T = 273^°К (0°C), g = 9.81 м/с². Для этих значений высота однородной атмосферы будет равна 7990 м.

Поскольку плотность однородной атмосферы постоянная, а давление с высотой убывает, то и температура ее, равная по уравнению состояния:

(2.17)

понижается.

Возьмем производную этого выражения и заменим правой частью основного уравнения статики. В результате получим:

°/100м, (2.20)

где – градиент вертикального изменения температуры.

• Таким образом, в однородной атмосфере температура воздуха с высотой убывает по линейному закону:

. (2.21)

Политропная атмосфера – атмосфера, в которой температура воздуха убывает с высотой по линейному закону.

Для политропной атмосферы справедливо выражение:

. (2.22)

Подставим это выражение в (2.13) и для сухого воздуха получим:

, (2.23)

проинтегрировав выражение (2.23) запишем:

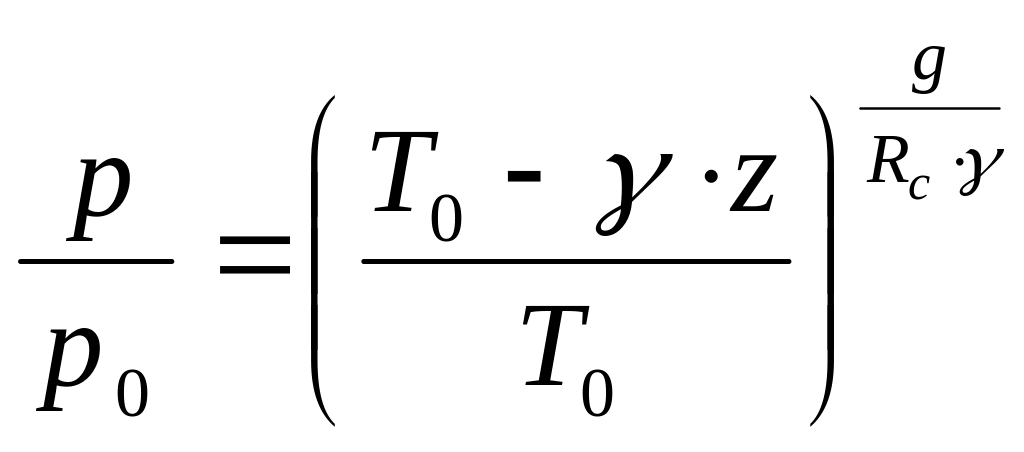. (2.24)

Это выражение является барометрической формулой для политропной атмосферы.

Высота политропной атмосферы определяется из выражения:

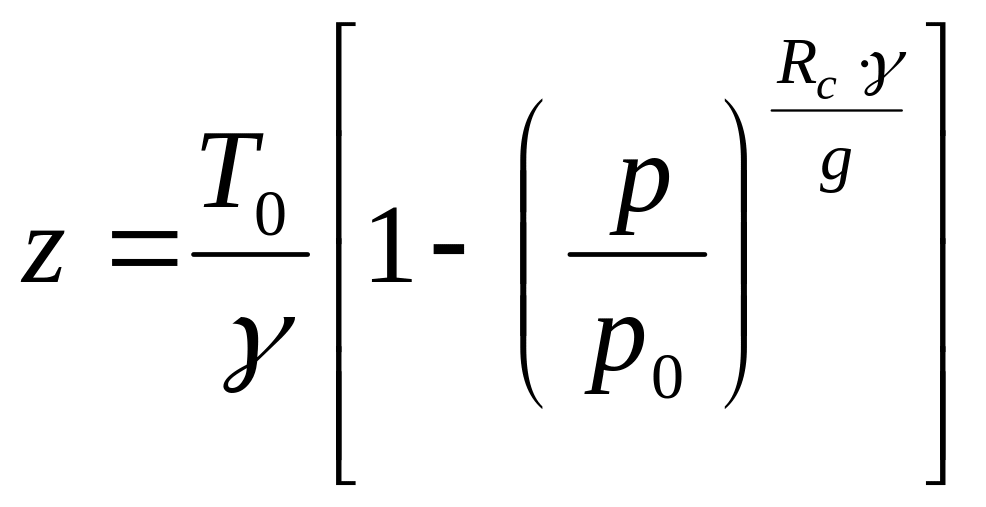. (2.25)

Высота политропной атмосферы при температуре Т₀=288°К (15°С) и градиенте вертикального изменения температуры С/100м равна:

44,3 км.

Реальная атмосфера

Выражение для изменения давления с высотой в реальной атмосфере определяется по формуле:

, (2.26)

где T_v среднее барометрическое значение температуры воздуха в слое. Выражение (2.26) известно в метеорологии как формула Лапласа.