§ 32 Примеры решения задач.
Задача 1
Мотоциклист через 5 с после начала движения приобрел скорость 54 км/ч. С каким ускорением двигался автомобиль? Какое расстояние он прошел при этом?
а-? s -? |
СИ |
Решение |
v0=0 м/с t1 =5 с v1=54км/ч |
15м/с |
Изобразим ситуацию, описанную в задаче, на рис.3.20: |
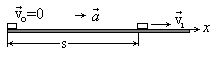
Рис.3.20
Скорость при равноускоренном движении находится по формуле:
v1= v0 + а t1
В нашем случае начальная скорость равна нулю, следовательно:
v1 = а t1
Отсюда а =
Проверим размерность:
Произведем вычисления: а =
Расстояние, которое при этом пройдет мотоциклист, найдем по формуле:
s =v0t+
С учетом того, что начальная скорость мотоциклиста равна нулю, получим, что:
s =
Так как а =
,
то s =
Проверим размерность:
Произведем вычисления: s
=
Ответ: а =
;
s =
Задача 2
Скорость автомобиля уменьшилась с 54 км/ч до 36 км/ч за 10 с. Запишите закон изменения скорости и уравнение перемещения.
v(t)-? s(t)-? |
СИ |
Решение |
v0=54 км/ч t1 =10 с v1= 36 км/ч |
15 м/с
10 м/с |
Сначала переведем единицы измерения скорости в СИ. |
Затем найдем величину ускорения машины:
a=
.
Теперь запишем закон изменения скорости:
v= v0 + а t =15 – 0,5t
Перейдем к записи уравнения перемещения:
s =v0t+ = 15t – 0,25t2
Ответ: v= 15 – 0,5t; s = 15t – 0,25t2.
Задача 3
Движение машины и велосипедиста описываются уравнениями х1=-100+10t и х2=40–5t+2t2. Запишите уравнения скоростей для обоих тел. На оси ОХ указать положение тел, направление их скоростей и ускорений в начальный момент. В какой момент времени скорости тел станут одинаковыми?
Решение
Сравнив уравнения движения обоих тел с законом изменения координаты, который выглядит так х =х0+ v0t+ , мы можем сказать следующее: начальные координаты тел равны х01= -100м и х02= 40м, начальные скорости v01= 10м/с и v01= -5м/с (тело движется в направлении, которое противоположно направлению, принятому за положительное), ускорение первого тела а1=0м/с2 (движение равномерное), ускорение второго тела а2=4м/с2. Так как уравнение для скорости выглядит следующим образом:
v=v0+at
то для первого тела имеем: v1 =10, а для второго v2 =-5+4t.
Теперь изобразим на оси ОХ положение тел, направление их скоростей и ускорений в начальный момент:
Рис.3.21
Для того, чтобы найти момент, когда скорости тел станут одинаковыми, приравняем v1 и v2.
10=-5+4t
Отсюда получим, что t=15 с. Значит через 15 с скорости тел станут одинаковыми.
Ответ: v1 =10, v2 =-5+4t, t=15 с
Задача 4
Написать уравнение движения материальной точки, если х0=10 м, v0=-2 м/с, а=0,8 м/с2. определите координату точки в момент времени 2 с и 5 с.
Решение
Воспользуемся уравнением движения материальной точки: х=х0+v0t+ . Подставив в это уравнение данные задачи получим:
х =10 – 2t+0,4t2
Определим координату точки через 2 с:
х1= 10 - 2·2+0,4·4=7,6 м
Определим координату точки через 5 с:
х2= 10 - 2·5+0,4·25=10 м
Следовательно, через 5 с после начала движения тело вернулось в исходное положение.
Ответ: х =10 – 2t+0,4t2; х1= 7,6 м; х2= 10 м.
Задача 5
Автобус, двигавшийся по проселочной дороге со скоростью 18 км/ч в течение 5 мин, выехал на асфальтированную дорогу и за 80 с увеличил свою скорость до 90 км/ч. Затем, двигаясь равномерно, автобус проехал по асфальту еще 3 км. Заметив остановку, водитель стал постепенно уменьшать скорость и через 50 с остановился. Определите ускорение автобуса при разгоне и торможении. Постройте график зависимости скорости от времени.
а1-? а2-? |
СИ |
Решение |
v1=18км/ч t1=5 мин v2=90км/ч t2=80c s3=3км t3=80c |
5 м/с 300с 25 м/с
3000м |
Данную задачу удобно разбить на несколько этапов. Сначала найдем ускорение автобуса при разгоне. Это мы сделаем, используя формулу |
Подставив значения скоростей и времени, получим:
Аналогично найдем ускорение при торможении:
Произведем вычисления:
Знак «-» означает что ускорение автобуса во втором случае направлено в сторону противоположную направлению принятому за положительное.
Прежде чем построить график зависимости скорости движения автобуса от времени его движения, определим время равномерного движения автобуса по асфальту.
По оси абсцисс будем откладывать время (масштаб 1 см -80 с), а по оси ординат – скорость (масштаб 1 см – 5 м/с). В результате получим график (см.рис.4.22).
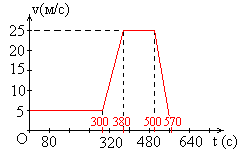
Рис.4.22
Попробуйте самостоятельно построить график зависимости скорости движения автобуса от времени, выбрав другой масштаб: оси абсцисс будем откладывать время (масштаб 1 см -40 с), а по оси ординат – скорость (масштаб 1 см – 2,5 м/с). Сравните два графика. Каким из них удобнее пользоваться?
Задача 6
опред ср.скорость при равноускоренном движении
Прежде, чем произвести вычисления переведем в СИ единицы измерения скорости и запишем в дано задачи.
v=2-3t, v=2+3t, найти ускорение, начальную скорость, построить график, по известным а и нач. скорости найти скорость конечн