§ 30. Средняя скорость

Движения тел, происходящие в реальной жизни, не являются равномерными. Чаще всего скорости тел в разные моменты времени разные. Такие движения называются неравномерными. Так, например, автобус, трогаясь с остановки, постепенно увеличивает свою скорость, а, подъезжая к остановке, наоборот уменьшает ее. Получается, что в разные моменты времени его скорость различна.

Еще раз напоминаем, что в курсе физики 7 класса мы рассматриваем только прямолинейное движение, при котором величина пройденного пути и величина перемещения одинаковы.

Если шарик будет скатываться по наклонному желобу вниз, то его скорость будет возрастать, а при движении этого же шарика вверх по желобу, его скорость будет уменьшаться (рис.3.16).

рис.3.16

Т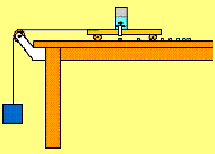 ележка, движущаяся по горизонтальной поверхности под действием груза, прикрепленного к ней через блок (рис.3.17), тоже будет двигаться неравномерно.

Для описания неравномерного движения вводят понятие средней скорости движения. рис.3.17

Под средней скоростью неравномерного прямолинейного движения понимают скорость такого равномерного прямолинейного движения, при котором за тот же промежуток времени будет совершено такое же перемещение (пройден такой же путь).

Поэтому, найти величину средней скорости можно, разделив величину всего перемещения (пути) на время, за которое оно было совершено, т.е.

Обращаем ваше внимание на то, что не следует путать среднюю скорость со средней арифметической скоростью, которую находят, как и любую среднюю арифметическую величину:

Пример: Автомобиль, двигаясь прямолинейно, прошел половину пути со скоростью 80 км/ч, а вторую половину со скоростью 20 км/ч. определите среднюю скорость на всем пути.

-?	рис.3.18
s1=s2=s/2

Изобразим ситуацию, описанную в задаче, на рисунке 3.18. По определению средняя скорость (1), где t – это все время движения. Оно складывается из времени движения на первой половине пути и времени движения на второй половине пути . Подставив эти значения времени в формулу (1), получим:

(2).

Подставив в формулу (2) численные значения, получим:

.

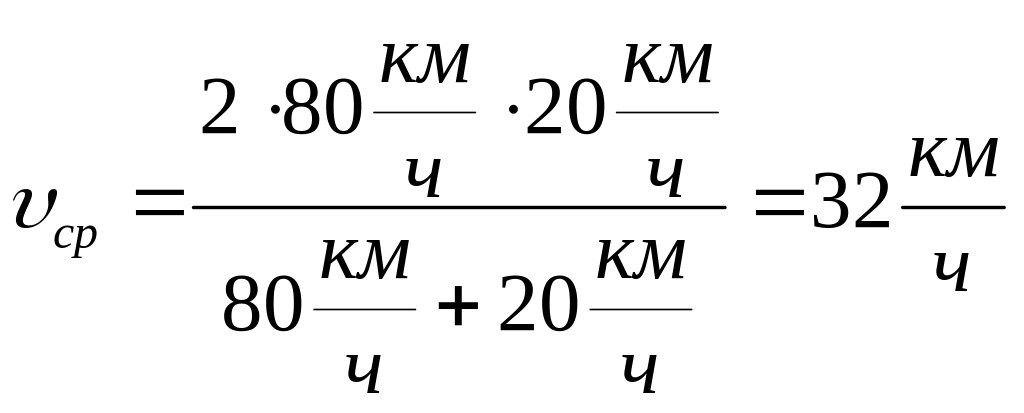Ответ:

Примечание: если рассчитать среднюю арифметическую скорость этого движения, то мы получим:

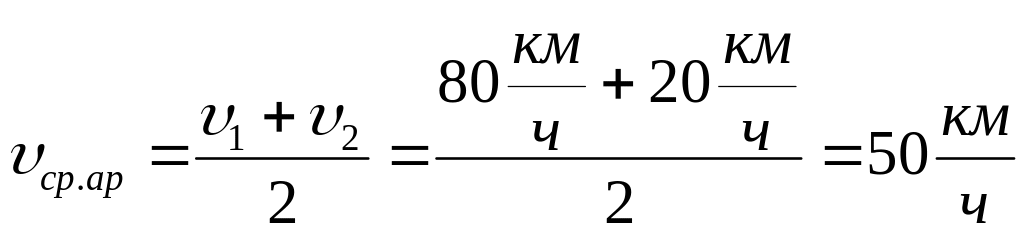
Это убеждает нас, что средняя скорость не равна средней арифметической скорости

Вопросы для самоконтроля:

1. Какое движение называют переменным? Приведите примеры такого движения.

2. Что вы понимаете под средней скоростью переменного движения? Для чего она была введена?

3. Как вы думаете, можно ли определить положение тела в любой момент времени, зная его среднюю скорость? Почему?

4. По какой формуле рассчитывают среднюю скорость неравномерного движения?

§ 31. Равнопеременное движение. Ускорение.

В этом параграфе мы рассмотрим частный случай неравномерного движения – равнопеременное движение.

Равнопеременным движением называют такое движение тела, при котором его скорость за любые равные промежутки времени изменяется на одну и ту же величину.

Для характеристики такого движения вводят особую физическую величину – ускорение.

Пуля вылетает из ствола охотничьего ружья за доли секунды и успевает за это короткое время увеличить свою скорость до 500 м/с. Значит ускорение пули очень велико. Поезд, трогающийся с места, за это же время изменяет свою скорость незначительно (примерно 1 мм/с). Видно, что ускорение поезда намного меньше ускорения пули.

Ускорение – это физическая величина, характеризующая быстроту изменения скорости, происшедшую за единицу времени.

Обозначается ускорение буквой . Ускорение – это векторная величина.

Из определения ускорения следует, что ускорение можно рассчитать по формуле:

(1)

Единицей измерения ускорения является (читается метр в секунду за секунду).

В случае прямолинейного движения направление скорости не изменяется. Поэтому величину изменения скорости находят как разность конечной и начальной скоростей тела, т.е.

Тогда величина ускорения будет равна:

(2)

В случае прямолинейного равнопеременного движения величина и направление ускорения не изменяется, т.е. .

В том случае, когда величина скорости будет постоянно возрастать, то величина ускорения будет положительной. Такое равнопеременное движение называется равноускоренным.

Если же величина скорости будет уменьшаться, то величина ускорения будет отрицательной. Такое равнопеременное движение называется равнозамедленным.

При равнопеременном движении скорость тела все время изменяется. А для того, чтобы найти скорость тела в любой момент времени можно воспользоваться формулой (2), из которой следует, что и, тогда скорость тела при равноускоренном движении в любой момент времени равна:

(3)

Из формулы (3) видно, что в случае равноускоренного движения скорость тела линейно возрастает со временем, а, следовательно, график этой зависимости будет выглядеть так, как изображено на рис.3.19а. Этот график называется графиком скорости.

рис.3.19а рис.3.19б

При равнозамедленном движении величина ускорения будет отрицательной и тогда формула (2) запишется так:

Отсюда получим что , скорость тела в любой момент времени будет равна:

(4)

Из формулы (4) видно, что в случае равнозамедленного движения скорость тела линейно уменьшается со временем. График этой зависимости выглядит так (см.рис.3.19б):

Следовательно, можно сказать, что как при равноускоренном (рис.3.19а), так и равнозамедленном движении (рис.3.19б) скорость тела изменяется со временем линейно.

Мы уже знаем, что величину перемещения (пути) при прямолинейном движении можно найти как площадь фигуры, ограниченной графиком v(t) и осями координат. Поэтому легко найти путь, пройденный телом при равноускоренном движении, используя график, изображенный на рис. 3.19а. Из графика видно, что площадь данной фигуры равна сумме площади нижнего прямоугольника s₁=v₀t и площади треугольника, равной половине площади верхнего прямоугольника s₂=(v-v₀)t/2. А т.к. v=v₀+at, то s₂=аt²/2. Тогда s=s₁+s₂. Т.е. s = v₀t + аt²/2.

Вопросы для самоконтроля:

1. Какое движение называется равнопеременным?

2. Что вы понимаете под ускорением?

3. В каких единицах измеряется ускорение?

4. Ученик, характеризуя движение поезда, сказал: поезд двигался с отрицательным ускорением. Что это означает?

5. Как рассчитывают скорость тела при равноускоренном движении?

6. Как рассчитывают скорость тела при равнозамедленном движении?

7. Постройте график скорости шарика начавшего скатываться с наклонной плоскости с ускорением 2 м/с².

8. Постройте график скорости поезда, который остановился через 40 с, имея начальную скорость 36 км/ч.

9. Как по графику скорости определить ускорение тела?