§ 29. Примеры решения задач

В этом параграфе мы рассмотрим примеры решения задач на механическое движение. Напоминаем вам, что прежде чем начать решать задачу, необходимо внимательно прочитать ее условие и представить явление, описанное в задаче.

Затем необходимо найти законы, описывающие это явление и записать эти законы на языке математики. После этого записываем условие задачи в краткой форме, принятой в физике. Желательно решение задач сопровождать рисунками, схемами или графиками. Желательно выразить единицы измерения физических величин в системе интернациональной СИ.

Задача 1

Самолет летит со скоростью 864 км/ч. Какое расстояние пролетит самолет за 12 мин?

s-?	СИ	Решение
v= 864км/ч t = 12 мин	240м/с 720 с	Сначала переведем единицы измерения физических величин

в систему СИ. Напоминаем, как выразить скорость и время в СИ:

v= 864 = .

t =12 мин = 12·60 с =720 с

После того, как оформлена краткая запись задачи, а единицы измерения переведены в СИ, приступаем к непосредственному разбору явления, описанного в задаче. А в задаче сказано, что самолет летит с постоянной скоростью, т.е. движение равномерное. Путь при равномерном движении можно рассчитать по формуле:

s=vt.

Теперь проверим размерность данной величины:

.

Произведем вычисления:

s = 240·720=172800 м = 172,8 км

Ответ: s = 172,8 км

Задача 2

Скорость автомобиля 72 км/ч, а скорость ветра 5 м/с. Какова скорость ветра в системе отсчета, связанной с автомобилем? Рассмотреть два случая: ветер а) встречный; б) попутный.

vотн-?	СИ	Решение
v1=72 км/ч v2=5 м/с		Сначала выразим скорость автомобиля в СИ:

v₁=72/3,6 м/с=20м/с

Перейдем в систему отсчета, связанную с автомобилем. В этой системе автомобиль покоится, земля будет двигаться со скоростью 72км/ч навстречу автомобилю, а значит и воздух вместе с землей движется с такой же скоростью в том же направлении. Тогда, воспользовавшись законом сложения скоростей, будем иметь

а)Ветер дует навстречу автомобилю, значит скорости складываются:

v_отн=(20+5)м/с=25 м/с

б)В случае попутного ветра, скорости вычитаются, т.к. в системе отсчета, связанной с автомобилем, ветер дует в сторону противоположную движению воздуха:

v_отн=(20 – 5)м/с=15 м/с

Ответ: v_отн1 =25 м/с; v_отн2 =15 м/с

Задача 3

Автобус и автомобиль движутся прямолинейно и равномерно в одном направлении со скоростями 50км/ч и 80км/ч. В начальный момент времени расстояние между ними 24 км. Через какое время автомобиль догонит автобус?

t-?	СИ	Решение
v1=50 км/ч v2=80 км/ч s= 24 км		Свяжем систему отсчета с автобусом. В этой системе отсчета скорость автомобиля

будет равна:

v_отн= v₂ – v₁

Фактически v_отн – это скорость сближения машин. Тогда до встречи автомобиль пройдет расстояние s= v_отн t. Отсюда:

t=

В данной задаче вычисления удобно производить не системе СИ.

Проверим размерность:

Произведем вычисления:

t =

Ответ: t =48 мин

Задача 4

Пассажир, прогуливаясь по перрону, замечает, что мимо трех вагонов, он проходит за 2 мин. Длина одного вагона 25 м. Определите скорость пассажира и время, в течение которого он пройдет мимо всего поезда, состоящего из 24 вагонов.

v-? t-?	СИ	Решение
t1 =2мин s0= 25м n1=3 n=24	120с	Считая, что пассажир идет по перрону равномерно, найдем его скорость

v = (1)

где s₁ – длина трех вагонов, s₀ – длина одного вагона

Произведем вычисления:

v =

Скорость пассажира можно рассчитать и по- другому:

v =

где n – число всех вагонов.

Отсюда найдем время t, за которое пассажир пройдет мимо всего состава:

t = (2)

Подставив в (2) значение скорости из (1), получим:

t =

Произведем вычисления:

t =

Ответ: t =16 мин

Задача 5

Катер отплывает от пристани, находящейся на берегу озера, и через 15 м его скорость становится равной 10 м/с. Определите координату катера через 20 с после этого, считая его дальнейшее движение равномерным.

х1-?	СИ	Решение
v= 10 м/с t1 = 20 с х0= 15 м		Движение катера равномерное, поэтому уравнение движения катера выглядит так:

х = х₀+vt

В нашем случае имеем:

х = 15+20t

Тогда координата катера к моменту времени t₁ будет равна:

х₁= 15м + 10м/с·20с= 215м

Ответ: х₁=215м

Задача 6

Из города А в город В со скоростью 72 км/ч выехал рейсовый автобус. Одновременно с ним из города В в город А со скоростью 48 км/ч выехал мотоциклист. Определите время и место встречи автобуса и мотоциклиста, если между городами 120 км.

х1-? t1-?	СИ	Решение
v1=72 км/ч v2=54 км/ч s= 120 км		Изобразим ситуацию, описанную в задаче, на рис.3.16:

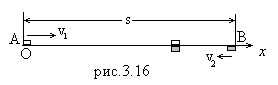
Свяжем систему отсчета с землей, а ее начало поместим в город А. Запишем уравнения движения обоих тел в выбранной системе отсчета:

х₁=v₁t (1) и x₂=s –v₂t (2)

В месте встречи координаты тел одинаковы, поэтому

v₁t₁=s –v₂t₁

Отсюда выразим время встречи

t₁= (3)

Проверим размерность

Произведем вычисления:

t₁=

Подставим формулу (3) в формулу (1) и найдем координату места встречи:

х₁=

Произведем вычисления:

х₁=

Ответ: t₁=1 ч; х₁=72 км.

Задача 7

Скорость катера относительно воды в n раз больше скорости течения реки. Во сколько раз больше по времени займет поездка на катере между двумя пристанями против течения, чем по течению?

t1/ t2-?	СИ	Решение
v к=n vт		Обозначим расстояние

между пристанями s, t₁ и t₂ – время движения катера против и по течению реки соответственно. Тогда относительно берега скорости катера против течения и по течению будут находиться как разность и как сумма скоростей катера и течения реки соответственно:

v₁= v _к – v_т и v₂= v _к + v_т

Расстояние между пристанями можно найти s= v₁ t₁(плывем против течения) и s= v₂ t₂(плывем по течению). Тогда

s=( v _к – v_т) t₁ =( n v_т – v_т) t₁= v_т (n – 1) t₁

s=( v _к + v_т) t₂=( n v_т + v_т) t₂= v_т (n + 1) t₂

Отсюда:

t₁= и t₂=

Следовательно,

Ответ:

Задача 8

По неподвижному эскалатору пассажир поднимается за 4 мин, а эскалатор неподвижно стоящего на нем пассажира поднимает за 2 мин. Сколько времени будет подниматься идущий вверх пассажир по движущемуся эскалатору?

t 3-?	СИ	Решение
t1= 4 мин t2= 2 мин		Обозначим длину эскалатора s. Тогда

Скорость пассажира равна: v₁= ;

Скорость эскалатора равна: v₂= ;

Скорость пассажира, идущего по движущемуся эскалатору равна: v₃= ;

Так как v₃= v₂+ v₁, то получим, что:

+ =

Отсюда следует, что t ₃=

Проверим размерность

Произведем вычисления:

t ₃=

Ответ: t ₃=80 с