
- •Глава 4. Движение
- •§ 20. Механическое движение
- •§ 21. Относительность механического движения
- •§ 22. Система отсчета
- •§ 23. Материальная точка
- •§ 24. Траектория
- •§ 25. Путь и перемещение
- •§ 26. Скорость
- •§ 27. Прямолинейное равномерное движение
- •§ 28. Графическое представление движения
- •§ 29. Примеры решения задач
- •§ 30. Средняя скорость
- •§ 31. Равнопеременное движение. Ускорение.
- •§ 32 Примеры решения задач.
- •Вопросы и задачи к теме
- •Лабораторная работа № 1 «Измерение пути и модуля перемещения»
- •Лабораторная работа № 2 «Наблюдение относительности движения сложение перемещений»
- •Лабораторная работа № 3 «Наблюдение прямолинейного равноускоренного движения и расчет средней скорости тела при этом движении»
§ 27. Прямолинейное равномерное движение
Тела могут перемещаться в пространстве по-разному: как с постоянно изменяющейся скоростью, так и с неизменной скоростью, как по криволинейной траектории, так и по прямолинейной.
Прямолинейным равномерным движением называется такое движение, при котором тело за любые равные промежутки времени совершает равные перемещения, не изменяя направление движения.
При таком движении скорость тела
остается неизменной как по величине,
так и по направлению, т.е.
![]() .
.
Последняя запись означает, что скорость
остается неизменной как по величине,
так и по направлению. Слово «const»
означает «постоянный». Если над символом
скорости
![]() не будет стоять стрелочка, т.е.
не будет стоять стрелочка, т.е.
![]() ,
то эта запись будет означать, что
постоянной остается только численное
значение скорости, а направление ее
может меняться.
,
то эта запись будет означать, что
постоянной остается только численное
значение скорости, а направление ее
может меняться.
Прямолинейное равномерное движение встречается в природе не часто, но в течение небольшого времени многие тела могут двигаться с неизменной скоростью по прямолинейной траектории.
Присмотритесь к окружающему вас миру, и вы сможете привести примеры прямолинейного равномерного движения.
М Проанализируйте движение тележки, изображенной на рисунке и опишите характер этого движения. Обоснуйте ход ваших рассуждений. |
Рассмотрим процесс перемещения электровоза по прямолинейному железнодорожному полотну. Пусть он движется равномерно. Тогда величина перемещения и пройденного пути будут одинаковыми. Найти их мы сможем по формуле:
![]() (1)
(1)
На рис.3.11 отмечено начальное положение электровоза хо и его конечное положение х.

Из рис.3.11 видно, что перемещение и путь (движение то прямолинейное) можно найти так:
![]() .
.
Следовательно, чтобы найти координату электровоза х в любой момент времени, необходимо к его начальной координате хо прибавить величину перемещения:
![]() (2)
(2)
Подставив, в формулу (2) перемещение из формулы (1), получим:
![]() (3)
(3)
Это выражение называется законом равномерного прямолинейного движения материальной точки.
По формуле (3) можно найти координату любого тела, движущегося прямолинейно и равномерно в любой момент времени.
Вопросы для самоконтроля:
Какое движение называется равномерным прямолинейным?
Каким образом рассчитывают путь при равномерном прямолинейном движении?
Что называется законом движения?
Как выглядит закон движения тела, движущегося равномерно и прямолинейно?
Опишите характер движения тела, закон движения которого выглядит так: х=-5+2t.
§ 28. Графическое представление движения
Любое движение можно изобразить графически. Это дает возможность представить движение более наглядно. Для этого по оси абсцисс откладываем время движения, а по оси ординат – значения координат тела в выбранном масштабе. Далее, используем закон движения тела, движущегося равномерно и прямолинейно:
,
и строим график зависимости координаты тела х от времени его движения t. Полученная линия покажет нам, как меняется координата тела со временем.
Для простоты рассмотрим случай, когда тело, находившееся в момент времени t=0 в точке с координатой хо=4 м, стало двигаться в положительном направлении координатной оси со скоростью =2 м/с. Закон движения этого тела будет выглядеть так:
![]() (1)
(1)
Из курса математики известно, что такая зависимость представляет собой прямую линию. А для того, чтобы построить прямую линию достаточно иметь только две точки, так как через две точки можно провести только одну прямую. Подставляя в формулу (1) два произвольных значения времени, например 0 с и 2 с, получим два значения координаты 4 м и 8 м (см. таблицу):
t (c) |
0 |
2 |
x (м) |
4 |
8 |
Таким образом, можно утверждать, что координата точки, движущейся равномерно и прямолинейно, является линейной функцией времени, что хорошо видно на рис.3.12
П о
графику, изображенному на рис.3.12 можно
«прочитать», что в момент начала
наблюдений тело находилось в точке с
координатой хо=4м и
двигалось в направлении, выбранном
положительным.
о
графику, изображенному на рис.3.12 можно
«прочитать», что в момент начала
наблюдений тело находилось в точке с
координатой хо=4м и
двигалось в направлении, выбранном
положительным.
Если по оси ординат откладывать значения скорости, а по оси абсцисс – время, то получим график скорости. В нашем случае он будет выглядеть так (см.рис.3.13)
По графику скорости легко определить путь, пройденный телом.
Д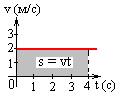 ля
этого нужно вычислить площадь фигуры,
ограниченной графиком скорости и линией
перпендикулярной оси времен и проходящей
через данное значение времени
(см.рис.3.14).
ля
этого нужно вычислить площадь фигуры,
ограниченной графиком скорости и линией
перпендикулярной оси времен и проходящей
через данное значение времени
(см.рис.3.14).
рис.3.14
В нашем случае :
![]()
П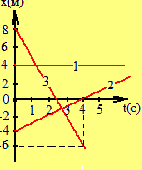 о
графику координаты тела легко описать
характер его движения. Попробуйте
описать, как двигались тела 1, 2 и 3,
графики движения которых даны на
рис.3.15.
о
графику координаты тела легко описать
характер его движения. Попробуйте
описать, как двигались тела 1, 2 и 3,
графики движения которых даны на
рис.3.15.
Рис.3.15
Вопросы для самоконтроля:
Что означает выражение «изобразите движение тела графически?
Объясните выражение «прочитайте график движения тела».
Как построить график координаты тела?
тело движется в отрицательном направлении со скоростью 5 м/с. Постройте график его скорости.
Как, используя график скорости, рассчитать путь, пройденный телом за определенное время?
На рис.3.15 приведены графики координат трех тел. Что означают точки пересечения этих графиков а) друг с другом; б) с осями координат?

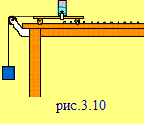 ы
же предлагаем вам рассмотреть следующий
случай, изображенный на рис.3.10.
ы
же предлагаем вам рассмотреть следующий
случай, изображенный на рис.3.10.