2.6. Агрегирование нормативных показателей

При моделировании межотраслевых связей важным является вопрос агрегирования нормативных показателей. Рассмотрим пример. Пусть задана таблица межотраслевых потоков для четырех отраслей (табл. 2.1).

Таблица 2.1

Производ. отрасль	Потребляющие отрасли				Конечный продукт	Валовой выпуск
	1	2	3	4
1	x11	x12	x13	x14	y1	x1
2	x21	x22	x23	x24	y2	x2
3	x31	x32	x33	x34	y3	x3
4	x41	x42	x43	x44	y4	x4

Определим параметры агрегирования при объединении второй и третьей отраслей. Выделим в табл. 2.1 отрасли, подлежащие агрегированию. Присвоим новой отрасли индекс k и составим другую таблицу, введя в нее отрасль k (табл. 2.2). Агрегированными окажутся те межотраслевые потоки, которые содержат индекс k.

Таблица 2.2

Производ. отрасль	Потребляющие отрасли			Конечный продукт	Валовой выпуск
	1	k
1	x11	x1k	x13	y1	x1
k	xk1	xkk	xk3	yk	xk
4	x41	x4k	x43	y4	x4

Определим поток из i-й отрасли в отрасль k. Поток x_ik объединит все потоки из i-й отрасли в отрасли, которые образовали k-ю отрасль. Для нашего случая

x_ik= i = 1,4.

Сформируем поток из k-й отрасли в j-ю. Поток x_ik объединяет потоки всех отраслей, направленных в j-ю отрасль, т. е. входящих в k-ю отрасль. Для нашего случая

j=1,4

Поток k-й отрасли на собственное воспроизводство включит все межотраслевые потоки, оставшиеся внутри этой отрасли, т.е.

Зная агрегированные потоки, найдем коэффициенты прямых затрат агрегированных отраслей. Тогда коэффициент прямых затрат i-й отрасли на воспроизводство единицы продукции j-й отрасли равен отношению потока из i-й отрасли к валовой продукции j-й отрасли:

i=1,k,4, j=1,k,,4.

Зная агрегированные потоки, найдем коэффициенты прямых затрат агрегированных отраслей. Тогда коэффициент прямых затрат i-й отрасли на воспроизводство единицы продукции j-й отрасли равен отношению потока из i-й отрасли к валовой продукции j-й отрасли:

i=1,2,3,4, j=1,2,3,4.

Далее сформируем оператор агрегирования Т. Для этого произведем деформацию единичной матрицы четвертого порядка (размерность единичной матрицы равна размерности исходной таблицы межотраслевого баланса) по следующему правилу: выделим в единичной матрице E те строки, номера которых совпадают с номерами агрегируемых отраслей, и просуммируем их. Результат внесем в k-ю строку матрицы Т. Все остальные строки переписываем в матрицу без изменения. Для нашего примера

Матрица Т есть результат «горизонтальной деформации» матрицы E.

По3строим деформированную весовую матрицу W. Для этого введем веса Wi, означающие вклад валовой продукции исходной i-й отрасли в валовую продукции отраслей, представленных в новой агрегированной таблице. Так, 1-я и 4-я отрасли в нашем примере (см. табл. 2.2) не подлежат агрегированию. Следовательно, . Составим весовую матрицу W:

Деформируем матрицу W по столбцам, объединив второй и третий столбцы. Тогда

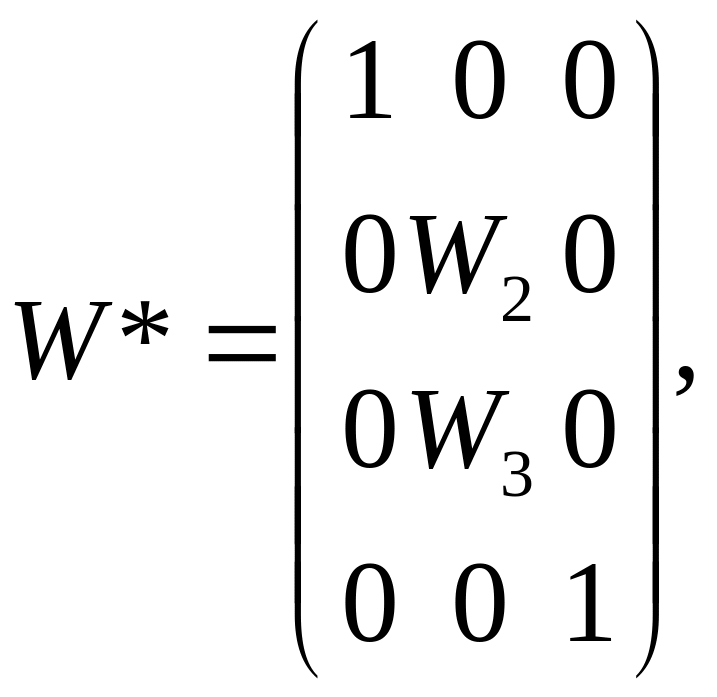
где W* – весовой оператор агрегирования.

Для получения матрицы коэффициентов прямых затрат с учетом агрегирования достаточно перемножить следующие матрицы:

A_агрег = TAW*.

Выводы

1. Анализ межотраслевого баланса дает комплексную характеристику процесса формирования и использования совокупного общественного продукта в отраслевом разрезе.

2. В основу схемы межотраслевого баланса положено разделение совокупного продукта на две части, играющие различную роль в процессе общественного воспроизводства, – промежуточный и конечный продукт.

3. Основной вопрос, возникающий в планировании производства на заданный период формулируется, как правило, следующим образом: при заданном векторе Y конечного потребления требуется определить необходимый объем валового выпуска, т.е. решить систему:

X – AX = Y, X ≥ 0. Условие неотрицательности X создает определенные трудности при исследовании вопроса о существовании решения системы.

4. Продуктивность модели Леонтьева полностью определяется величиной фробениусова собственного числа λ_A матрицы А коэффициентов прямых затрат.

5. Статическая модель Леонтьева может быть использована для рассмотрения вопрос использования и распределения трудовых ресурсов.

6. При моделировании межотраслевых связей важным является вопрос агрегирования нормативных показателей.

22