3.5. Пояснения к решению задач на трехфазный ток

В задачах на трехфазный ток подразумевается, что симметричная нагрузка, соединяемая «звездой» или «треугольником», при ее включении в питающую сеть подключается к одному и тому же линейному напряжению (рис. 21). Ток, протекающий по фазной нагрузке, называется фазным током. Падения напряжения на сопротивлениях нагрузки называют фазным напряжением. Между величинами фазных напряжений, токов и сопротивлений нагрузки при любом их соединении выполняется соотношение U_Ф=I_ф R.

Рис. 21

4. Примеры решения задач

Задача 1

Электрическая цепь, составленная из источников ЭДС E₁ с последовательно подключенным сопротивлением R₁ = 160 Ом и E₂ подключена к сопротивлению потребителя R_потр (рис. 22). Источники ЭДС обладают внутренним сопротивлением. Определить ток, протекающий по сопротивлению Rпотр., если падение напряжения на сопротивлении R_потр, равно 11В. Направления токов указаны на рис. 22.

Дано: Е₁=15 В; Е₂=165 В; R₀₁ = 9 Ом; R₀₂=11 Ом; U_нагр =11 В.

Определить ток I.

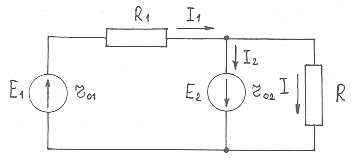
Рис. 22

Решение

Ход решения. Применяя второй закон Кирхгофа для контура E₁R₁E₂R₀₁R₀₂, найдем I₁. Применяя первый закон Кирхгофа для верхнего узла, рассчитаем I.

По второму закону Кирхгофа для замкнутого контура E₁R₁E₂r₂r₁ имеем

E₁ + E₂ = I₁ R₀₁ + I₁R₁ + U_нагр;

где I₁ – ток, протекающий по сопротивлениям R₀₁ и R_lt тогда

I₁ = (E₁ + E₂ – U_нагр) / (R₀₁ + R₁).

По закону Ома ток, протекающий по сопротивлению r₂ равен

I₂ = U_нагр / R₂

По первому закону Кирхгофа: I₁ = I₂ + I, откуда I = I₁ – I₂.

Подставим найденные выражения для I₁ и I₂:

;

Проверяем размерность I = B / Ом = А.

Подставим исходные данные

I = (165 + 15 – 11) / (9 + 160) – 11/11 = 1 – 1 = 0 А

Ответ: по сопротивлению R_нагр ток не течет (равен нулю).

Задача 2

Активное сопротивление R индуктивность L соединены последовательно (рис. 23). При изменении входного напряжения в два раза ток изменился на 1 А. Построить треугольник напряжений (частота источника тока равна 50 Гц).

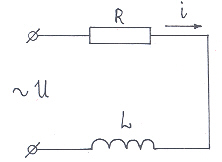
Рис. 23

Дано: R = 10 Ом; L = 42,5мГ = 4,25 10^-2 Г; U / U₁ = 2; I – I₁= 1A; f =50Гц.

Определить: U_R, U_L,и U_общ построить треугольник напряжений.

Решение

Ход решения: определим ток в цепи, затем рассчитаем напряжения на элементах схемы U_R, U_L и входное U общ.

При изменении напряжения в 2 раза ток изменится в два раза (по закону Ома), следовательно, ток в цепи равен 2 А, то есть I = 2 А.

Индуктивное сопротивление определяется по зависимости

X_L= L=2  f L,

где =2 f; f - частота переменного тока; L - индуктивность.

Полное сопротивление определяется выражением:

;

Напряжение на элементах схемы:

U_R=I х R, U_L=I х X_L=I х 2fL

Проверяем размерность

Входное напряжение можно определить двумя способами

Или

Подставим исходные данные:

U_R=2 · 10=20 B;

U_L=2 2  50 4,25 10^-2=26,6 B;

Треугольник напряжений строится с указанием масштаба (см. рис. 24).

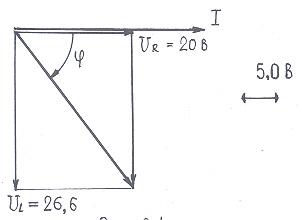
Рис. 24

Напряжение на активном сопротивлении совпадает по фазе с током, а напряжение на индуктивности опережает ток на 90º.

Задача 3

Активное сопротивление R и емкость С соединены параллельно (рис. 25). По активному сопротивлению протекает переменный ток с амплитудой I_R=3,2 и частотой f=50 Гц. Построить треугольник токов.

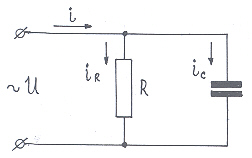
Рис. 25

Дано: R = 7,5 Ом; С=318,5 мкФ = 3,185-10 ^-4 Ф; I_R =3,2 А; f = 50 Гц.

Определить: I_C, I.

Построить треугольник токов.

Решение

Ход решения: определяем напряжение U, общее для R и С; по нему рассчитываем ток I_C, вычисляем I.

Так как элементы схемы соединены параллельно, то напряжение на емкости и активном сопротивлении одинаковое.

По закону Ома это напряжение будет

U = I_R R.

Емкостное сопротивление

X_C=1/C=1/2  fC,

тогда ток в емкости будет

I_C=U/X_C=U 2  fC= I_R R 2  fC.

Проверка размерности

I_C=A Ом Гц Ф= В 1/С К_л/В=А.

Полный ток определяется выражением

или

,

где

.

Подставляем исходные данные:

I_C=3,2 7,5 2 3,14 50 3,185 10^-4=2,4 A,

Треугольник токов (строится с указанием масштаба) (рис 26).

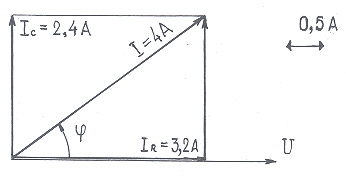
Рис. 26

Вектор тока, протекающего по активному сопротивлению, совпадает с вектором напряжения по фазе, а вектор тока на емкости опережает вектор напряжение на 90º.

Задача 4

Определить внутреннее сопротивление вольтметра R_пр с током полного отклонения I =10 мА, если добавочное сопротивление R_доб = 9980 Ом и при измерении напряжения U₁=50 В стрелка прибора отклонилась до половины шкалы (рис. 27).

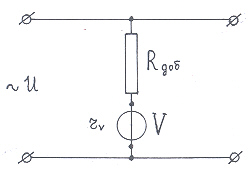
Рис. 27

Дано: I = 10 мА = 10^-2 А; R_доб = 9980 Ом; U₁= 50 В; I₁ = I/2.

Определить : R_nр.

Решение

Ход решения: определить напряжение, измеряемое вольтметром U и по закону Ома с учетом, что R_ï и R_д соединены последовательно, определить R . Напряжение, при котором произойдет полное отклонение стрелки прибора

U = 2U_1,

так как при напряжении U₁ стрелка отклонилась до половины шкалы прибора. Это напряжение складывается из напряжения на приборе Uï и напряжения на добавочном сопротивлении U_д.

U = U_п + U_д.

Так как добавочное сопротивление включено с прибором последовательно, то по ним течет ток полного отклонения

2U₁ = I (R_пр+ R_доб),

где R_пр и R_доб – сопротивления прибора и добавочное, тогда R_пр= (1U₁-I·R_др )/I .

Проверка размерности: R_п = В/А =Ом.

Подставим исходные данные:

R_пр = (2 · 50 - 10^-2 · 9980) / 10^-2 = 20 Ом.

Ответ: сопротивление прибора равно R_пр = 20 Ом.

Задача 5

Нагрузка трехфазной цепи соединена по схеме «звезда», при этом величина фазного тока равна одному амперу. Определить величину линейного тока при соединении данной нагрузки по схеме «треугольник», учитывая условие уменьшения величины в два раза.

Дано: I_ф1зв= 1А; R₂= R₁/2.

Определить: ток I_л2тр.

Нарисовав схемы соединения нагрузок «звездой» и «треугольником» (рис. 15), проставим индексы условных обозначений.

Ход решения: определяем фазное напряжение при соединении «звездой», а затем и линейное. По линейному напряжению определяем линейные токи при соединении «треугольником» нагрузок R₂.

Фазные напряжения при соединении симметричной нагрузки «звездой» определяются выражением

U_ф1зв = I_{ф 1зв} ·R₁.

Тогда линейные напряжения определяются:

При соединении нагрузок «треугольником» , тогда фазные токи будут .

Линейные токи при соединении нагрузок «треугольником»:

Подставив исходные данные, получим ответ.

Ответ. Линейные токи при соединении нагрузок «треугольником» будут равны 6 А.

Задача 6

Определить количество витков в первичной обмотке трансформатора, если к ней подведено напряжение U₁, напряжение холостого хода во вторичной обмотке U_2xx, число витков во вторичной обмотке W₁. Определить коэффициент полезного действия ή, если в рабочем режиме потребляемая трансформатором мощность P₁, при напряжении во вторичной обмотке U₂ и токе I₂.

Дано: U₁=127 В; U_2xx=8В; P₁=12 Вт; U₂=7,9 В; I₂= 1,43 A; n₂= 168.

Определить: W₁ и .

Решение

Нарисовать схему трансформатора (рис. 28).

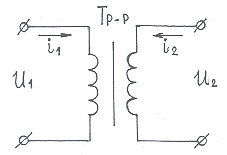
Рис. 28

Ход решения. Определяем коэффициент трансформации через напряжение холостого хода и вычисляем число витков в первичной обмотке. КПД трансформатора определим из соотношения мощностей отдаваемой и потребляемой трансформатором. Количество витков в первичной обмотке может быть определено по формуле

,

где К – коэффициент трансформации определяется через напряжения холостого хода .

Следовательно, .

Подставим исходные данные:

Коэффициент полезного действия равен отношению мощностей при включении трансформатора на нагрузку

где Вт.

Тогда

Ответ: количество витков в первичной обмотке равно 2 667; коэффициент полезного действия трансформатора  = 94 %.