3. Пояснения к решению задач
3.1. Цепи постоянного тока
При решении задач с источником постоянного тока необходимо на первом этапе упростить предложенную схему до одного сопротивления RЭ (рис. 19).
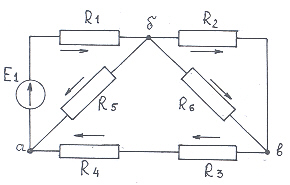
Рис. 19
При
последовательном соединении:
Ом.
При
параллельном соединении:
Ом;
Далее
определим величину тока, протекающего
по отдельным участкам цепи:
;
Падение напряжений на участке а-б:
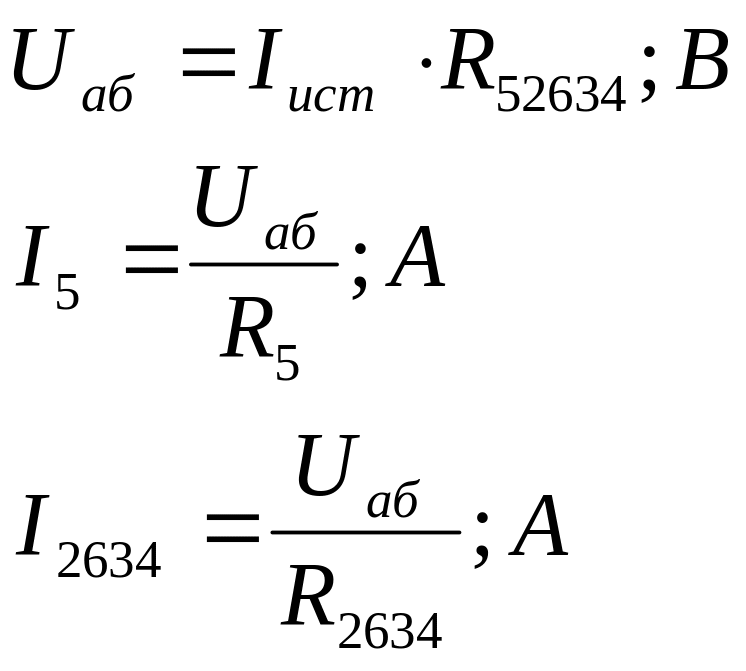
Проверка:
;
Падение напряжений на участке б-в:
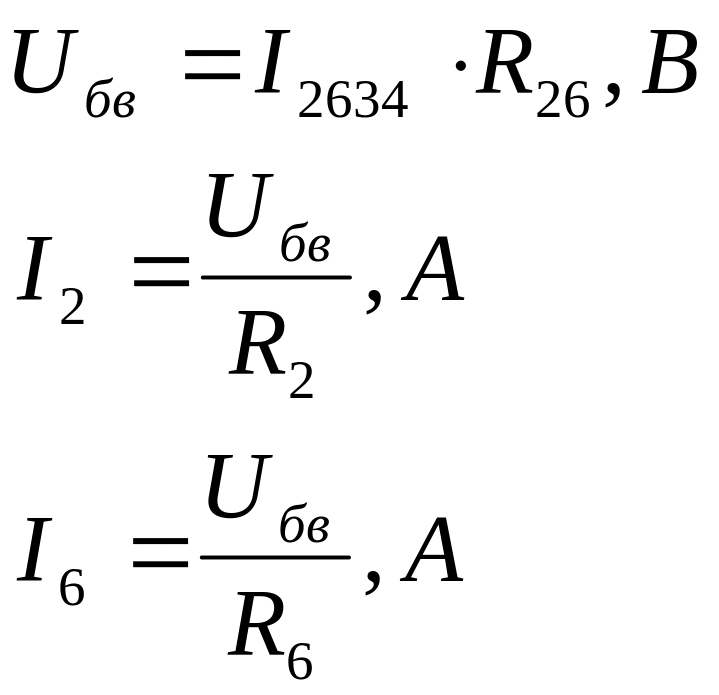
Проверка:
.
Определяем баланс мощностей:
Мощность потребителя можно рассчитать по формулам:
;
.
3.2. Цепи переменного тока
При решении задач с цепями переменного тока необходимо помнить, что законы электрических цепей постоянного тока продолжают действовать, но только в геометрической редакции. Это объясняется появлением двух видов нагрузки в цепях переменного тока (активной и реактивной) и появлением угла сдвига.
Первый
закон Кирхгофа в векторной форме:
Второй закон Кирхгофа в векторной форме:
3.3. Резонанс напряжений (последовательное соединение потребителей) и токов (параллельное соединение потребителей) напряжений
Решая задачи на резонанс напряжений нужно помнить, что при резонансе реактивное сопротивление контура равно нулю, так как XL=XC. В результате все напряжение, приложенное к контуру, падает на активном сопротивлении. Ток в схеме при резонансе равен:
,
так как
,
где U – напряжение, подводимое к схеме; r – активное сопротивление.
При
резонансе напряжений падения напряжения
на индуктивности и емкости будут
равны между собой (
;
Upc=UpL;
IpXc=IpXL;
UXc/R=UXL/R;
UXC
/R=UXC
/R)
и определяются
только параметрами Хс
и XL.
При этом
значения ∆UL
и ∆UC
могут
быть существенно больше Uобщ
(подобное явление
в цепях переменного тока часто называют
резонансом напряжений).
Решая задачи на резонанс токов, нужно помнить, что при данном резонансе токи в реактивных сопротивлениях могут быть бесконечно большими, но суммарный ток в схеме зависит только от r и определяется по закону Ома:
;
,
где U – напряжение, подводимое к схеме, r – активное сопротивление контура.
3.4. Пояснения к решениям задач по электрическим измерениям и расширению пределов измерений приборов
При включении в схему амперметра (рис. 20) ток, протекающий по сопротивлению R, уменьшится вследствие того, что амперметр обладает собственным внутренним сопротивлением rА. Напряжение на зажимах батарей будет отличаться от истинного значения Е, так как ЭДС имеет собственное внутреннее сопротивление r0.
Относительная ошибка самого прибора или приборная ошибка определяется выражением
=к Ан/А,
где к – класс точности прибора в процентах, Ан – верхний предел измерения прибора, А – значение электрической величины, измеренное прибором.
При расчете шунта амперметра необходимо учитывать, что ток через прибор должен остаться прежним предельным, а остальной – ответвляется по сопротивлению шунта (рис. 13). При расчете добавочного сопротивления к прибору для измерения напряжения необходимо учитывать, что напряжение на приборе Uп должно остаться прежним предельным, а остальное должно «гаситься» на добавочном сопротивлении Rд (рис. 20).
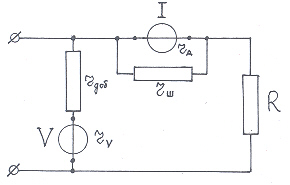
Рис. 20