Порядок розрахунку

1. Накреслити схему, яка відповідає заданому варіанту.

2. Визначити: а) повні опори віток;

б) активні та реактивні провідності віток;

в) активні та реактивні складові струмів віток;

г) активну та реактивну складові струму у нерозгалуженій

частині кола;

д) струми віток;

ж) активну, реактивну та повну потужності кола.

3. Побудувати векторну діаграму струмів.

ПРИКЛАД 7. Для електричного кола (див. рис. 14) за умови, що , необхідно накреслити схему електричного кола для заданого варіанта; визначити струми у вітках; визначити активну, реактивну та повну потужності; побудувати векторну діаграму струмів.

ДАНО: B ; ; Ом ;

Ом ; Ом ; ; Ом ; Ом ;

.

РОЗВ’ЯЗУВАННЯ. Накреслимо схему електричного кола для заданого варіанта (рис. 16).

Визначимо повні опори віток:

Ом ;

Ом ;

Ом .

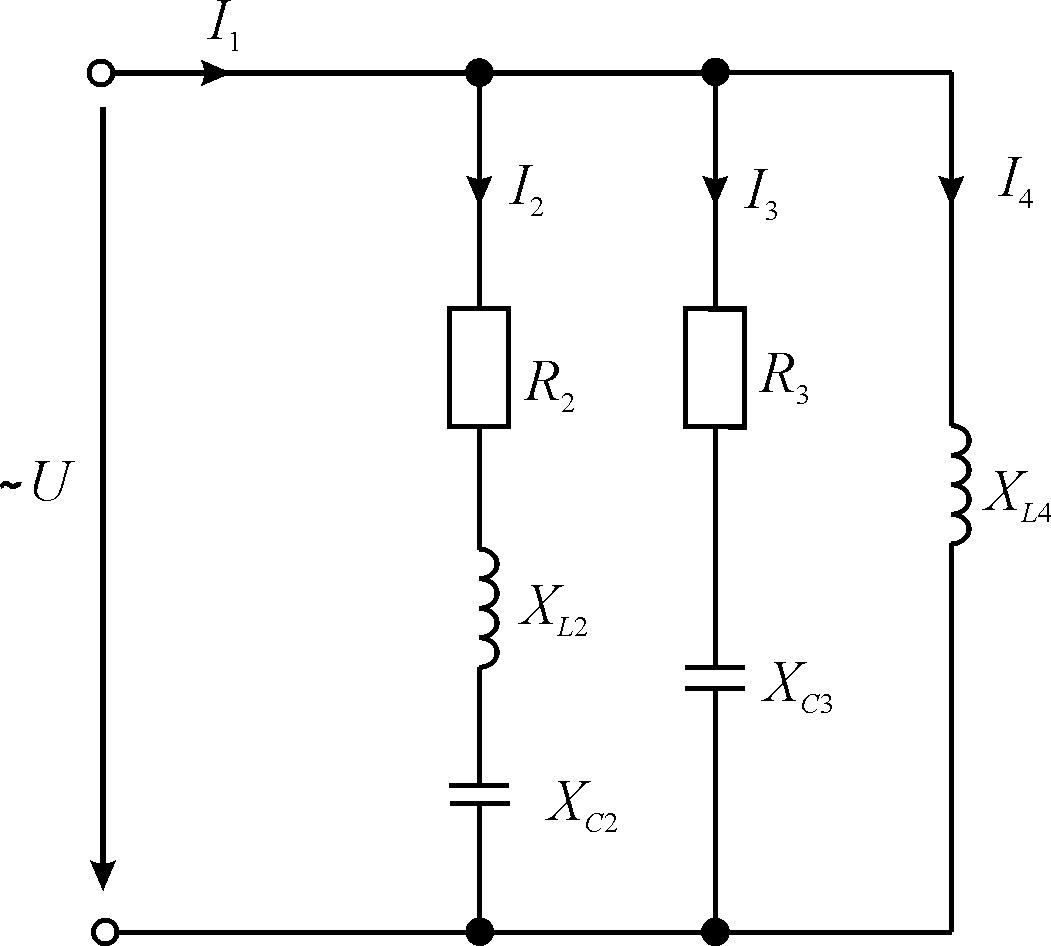
Рис. 16

Визначимо активні та реактивні провідності віток:

См ; См ;

См ; См ;

; См ;

Тоді активні та реактивні складові струмів віток дорівнюють:

A ; A ;

A ; A ;

; A .

Визначаємо активну та реактивну складові струму у нерозгалуженій частині кола: A ;

A .

Визначаємо струми віток:

Визначаємо активну , реактивну та повну потужності кола:

Вт ;

Вт ;

Вт;

вар ;

вар;

вар;

вар;

Побудуємо векторну діаграму. Масштаб напруги В/см; масштаб струмів А/см. Векторна діаграма зображена на рис. 17.

Рис. 17

Задача 6 розрахунок лінійного електричного кола однофазного синусїдного струму комплексним методом

В електричному колі (див. рис. 14) :

1. Накреслити схему для заданого варіанта.

2. Визначити діючі значення напруг та струмів на всіх ділянках кола при

частоті Гц i напрузі на затискачах кола В.

3. Побудувати векторну діаграму струмів та напруг.

4. Визначити активні, реактивні та повні потужності кожної ділянки і

усього кола.

5. Скласти баланс потужностей.

Числові значення наведені у табл. 5.

ПРИМІТКА: вибір варіанта у табл. 5, як i в задачі 2.

МЕТОДИЧНІ ВКАЗІВКИ

У комплексному методі розрахунку електричних кіл синусоїдного струму ЕРС, напруги, струми та опори подають у вигляді комплексних величин. Комплексні діючі значення величин, які змінюються за синусоїдним законом, позначають відповідними великими літерами, які підкреслюють рискою: , , . Для позначення модулів цих величин використовують ті ж літери, але без підкреслення рискою : , , .

Комплексний опір позначають прописною буквою (підкресленою), комплексну провідність − буквою (підкресленою). Повний опір позначають як , а повну провідність – .

Комплексні числа записують в одній з наступних форм :

– алгебраїчна;

– тригонометрична;

– показникова;

– полярна, де

– модуль комплексного числа;

– аргумент комплексного числа;

– уявна одиниця, розглядається як оборотний

множник, множення на який рівнозначне повороту

відрізка (без зміни, його величини) на

кут проти годинникової стрілки, тобто

.

Якщо напруга i струми змінюються за законом синуса:

; , де

, , , – відповідно миттєві значення i амплітуди напруги та струму; – початкові фази напруги та струму (початкові фазові кути) ;

– кутова частота, , де – частота мережі.

Ці величини у комплексній формі запишуться у вигляді:

, де

Комплексний опір кола, який складається з послідовно ввімкнених , , :

, де

; ; .

Комплексна потужність

, де

– повна потужність ;

– кут зсуву між струмом та напругою;

– активна потужність;

– реактивна потужність :

якщо , то i ; якщо ,то .

– спряжений комплексний струм, відрізняється від знаком перед уявною частиною, отже, перед аргументом (якщо , то ) ;

та – скорочений запис термінів: real – реальний, дійсний i imaginary – уявний.

Між , , існує співвідношення .