Задача 4 розрахунок нерозгалуженого кола синусоїдного струму

Напруга на затискачах кола, яке зображено на рис. 10, змінюється за законом . Амплітудне значення і початкова фаза напруги, а також значення активних , індуктивних і ємнісних опорів наведені в табл. 4. Частота мережі Гц.

Необхідно:

а) накреслити схему кола, яка відповідає заданому варіанту;

б) визначити напругу на ділянці ab і закон її зміни;

в) визначити активну, реактивну та повну потужності, які споживаються

колом із мережі;

г) побудувати векторну діаграму.

ПРИМІТКА: Вибір варіанта в табл. 4, як i в задачі 2.

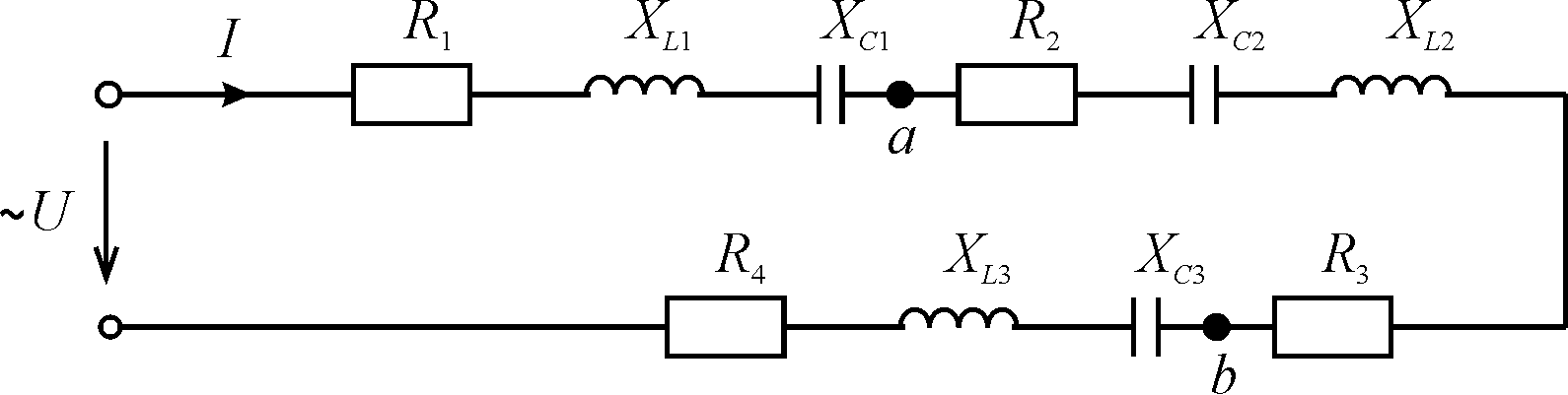
Рис. 10

Таблиця 4

Група даних	А							Б
Варіант	, B	, град	R1, Ом	XL1, Ом	XC1, Ом	R2, Ом	XL2, Ом	XC2, Ом	R3, Ом	XL3, Ом	XC3, Ом	R4, Ом
1 2 3 4 5 6 7 8 9 0	320 260 280 270 230 300 280 260 250 240	75 60 45 30 15 -75 -60 -45 -30 -15	10 14 15 5 5 0 10 0 7 8	14 0 10 0 0 0 7 20 5 0	0 5 0 0 10 7 0 5 40 20	10 0 0 10 0 14 5 0 5 0	0 30 35 0 15 8 35 0 0 5	8 35 0 0 5 12 30 35 0 15	14 5 0 5 0 8 35 0 0 5	7 0 5 40 20 14 5 0 5 0	0 7 20 5 0 7 0 5 40 20	0 10 0 7 8 0 7 20 5 0

Методичні вказівки

В електротехніці найбільш розповсюджені електричні кола зі струмами та напругами, що змінюються у часі. Якщо крива зміни струму у колі описується синусоїдою, то він називається синусоїдним. Значення змінних електричних величин (струму, напруги, ЕРС), що розглядаються в конкретні моменти часу, називаються миттєвими й позначаються малими літерами латинського алфавіту (i, u, e). Найбільші миттєві значення називають амплітудами ( , , ). Аналітично будь які синусоїдні електричні величини записують у вигляді . Тут – кутова частота, початкова фаза коливань, що показує значення струму в момент , – частота мережі ( = 50 Гц), Т – період коливань.

У практичних розрахунках струм i, який змінюється за часом , напругу u та ЕРС e замінюють діючими величинами відповідно I, U, E. Діючими називається такий незмінний у часі струм, який виділяє в опорі R за період Т ту ж кількість енергії, що і змінний за синусоїдним законом струм.

Величини I , U, E визначають за формулами :

; ; .

Вимірювальні прилади електромагнітної i електродинамічної систем показують діючі значення синусоїдних величин.

Синусоїдні величини можна подавати у вигляді: тригонометричних функцій, обертовими векторами, комплексними числами.

Елементи електричних кіл синусоїдного струму характеризуються параметрами: активним опором R , індуктивністю L і ємністю C.

Ці параметри впливають на величину та початкову фазу синусоїдного струму. Елементи L і C називають реактивними і їх вплив на величину синусоїдного струму ураховується реактивними опорами:

Ом.

Схема послідовного з’єднання елементів , L, C зображена на рис. 11, а.

Рис. 11

Оскільки напруга на затискачах такого кола визначається за другим законом Кірхгофа для миттєвих величин , у векторному вигляд (рис. 11, б) отримаємо . Вектор співпадає з вектором струму , вектор випереджає струм на кут , вектор відстає від вектора струму на кут . Отже, між векторами і кут . На рис. 11,б. зображена векторна діаграма, коли , тобто .

Величину напруги U визначаємо із трикутника a, b, c (рис. 11, б):

.

Виразимо складові напруг через струм та опори, тоді отримаємо

або

– закон Ома для кола з послідовним з’єднанням елементів R, L ,C , де повний опір кола, Ом; – реактивний опір кола, Ом.

Кут зсуву між струмом та напругою визначимо із трикутника опорів

(рис. 11, в) . Якщо миттєва величина струму

, то напруга на затискачах кола змінюється за законом

Якщо усі сторони трикутника напруг abc помножити на струм, то отримаємо подібний йому трикутник потужностей (рис. 11. г). Тут потужності кола:

– активна;

− реактивна потужність може бути додатною і від’ємною в залежності від знака кута φ. При індуктивному характеру вхідного опору (φ > 0) – реактивна потужність додатна, а при ємнісному (φ < 0) – від’ємна.

– повна потужність. Прийнято активну потужність вимірювати у ватах (Вт), реактивну у вольтампер реактивний (вар), повну у вольтамперах (ВА).

ПРИКЛАД 6. Для електричного кола (рис. 10) : накреслити схему кола, яка відповідає заданому варіанту, знайти діючі значення струму та напруги на усіх елементах кола i на ділянці ab, а також закон зміни струму i та напруги ; визначити активну, реактивну та повну потужність кола ; побудувати векторну діаграму.

ДАНО: B ; Ом; Ом;

; Ом; Ом.

РОЗВ’ЯЗАННЯ:

Схема кола, що відповідає заданому варіанту, зображена на рис. 12.

Рис. 12

Визначаємо діюче значення напруги на затискачах кола

Повний опір кола , де Ом ; Ом ; Ом , тоді

Діюче значення струму в колі: A.

Амплітудне значення струму .

Оскільки закон зміни напруги на затискачах кола

то миттєве значення струму ,

де ;

тоді , де .

Діюче значення напруги на ділянці ab : ,

де

Тоді B.

Амплітудне значення напруги на ділянці ab :

Закон зміни напруги : де

Тоді

Активна потужність, яка споживається колом із мережі,

Вт;

реактивна потужність ;

повна потужність ВА. Для побудови векторної діаграми треба визначити спади напруг напруги на окремих елементах кола:

B; B;

B; B;

B.

Побудуємо векторну діаграму. Вибираємо масштаб струму A/см;

напруги B/см. Векторна діаграма зображена на рис. 13.

Рис. 13