2.6 Задание граничных условий

Граничные условия, используемые в моделировании можно разделить на два типа: искусственные и естественные. Естественные граничные условия накладываются на искомую функцию, в то время как искусственные на ее производные. Естественные граничные условия появляются при работе с исходной математической моделью.

С точки зрения МКЭ искусственные граничные условия – это граничные условия, влияющие непосредственно на степени свободы модели, и являются искусственным ограничением для перемещения. При этом ограничения могут быть наложены в одном, двух или трех направлениях на узлы сетки. В теории упругости эти ограничения называются также кинематическими. Примером в ОМД может быть ограничение течения металла через рабочую поверхность штампа. Ограничение создаётся автоматически программой расчета.

Естественные граничные условия накладываются на вектор усилий напряжений. К этим условиям относят различные внешние силовые воздействия, действующие на точки или поверхности тела. Обычно такие граничные условия называют силовыми граничными условиями. Примером в ОМД могут быть силовые условия деформирования металла.

На практике приходится сталкиваться еще и со смешанными граничными условиями. В этом случае в данной точке поверхности тела задаются напряжения и перемещения. Наиболее распространенный пример таких граничных условий это задание плоскостей геометрической симметрии при решении задач деформирования осесимметричных тел. При решении задач по деформированию тел с геометрической симметрией смешанные граничные условия заключаются в равенстве нулю нормальных перемещений и равенству нулю касательных напряжений в узлах КЭ лежащих на плоскости симметрии.

На практике задание любых граничных условий являются важным элементом моделирования. Задание граничных условий должно отвечать следующим требованиям.

• Граничные условия не должны быть абсурдны по своей сути – например, при изучении процесса прикладывать усилие и фиксировать перемещение в одном и том же направлении не имеет смысла, нет смысла также фиксировать все перемещения в узлах дискретной модели (рисунок 26).

• Должно быть соответствие действия граничных условий на реальном теле и на модели как по усилию так и по перемещению.

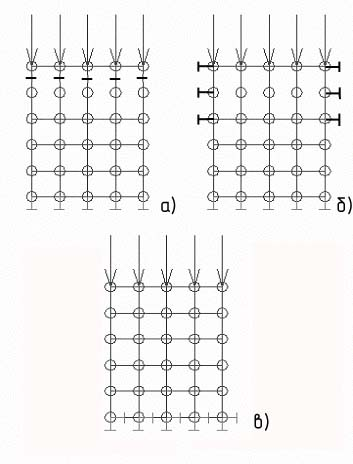
Рисунок 26 – Приложение граничных условий по усилию: а – неверное,

б – используемое для описания перемещения участка модели по направляющим, в – используемый для описания заделки

Следует заметить то, что граничные условия прикладываются к узлам дискретной модели и наибольшее число граничных условий, которое можно применить к каждому узлу это либо 3 силы, либо 3 перемещения. Число граничных условий должно быть обоснованно и минимально необходимо /14/.

Задание ограничений в современных программах очень упрощенно, например, для задания плоскостей симметрии при осадке достаточно указать поверхность симметрии на теле модели, а система сама распознает и накладывает ограничения на те узлы, которые принадлежат к этой плоскости. В случае использования программы граничные условия могут быть приложены к узлу, линии, поверхности или объему, но следует помнить, что с линии, поверхности и объема граничные условия будут перераспределенными на узлы.