Государственное образовательное учреждение высшего профессионального образования “Самарский государственный аэрокосмический
университет имени академика С.П. Королева”
Ф.В. Гречников, И.П. Попов, А.Г. Шляпугин
МОДЕЛИРОВАНИЕ ОБЪЕКТОВ В МЕТАЛЛУРГИИ
И ОБРАБОТКЕ МЕТАЛЛОВ ДАВЛЕНИЕМ
САМАРА 2007
Министерство образования и науки российской федерации
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования “Самарский государственный аэрокосмический
университет имени академика С.П. Королева”
Ф.В. Гречников И.П. Попов, А.Г. Шляпугин
МОДЕЛИРОВАНИЕ ОБЪЕКТОВ В МЕТАЛЛУРГИИ
И ОБРАБОТКЕ МЕТАЛЛОВ ДАВЛЕНИЕМ
Учебное пособие
САМАРА 2007
УДК 621.73.681.3
Основы компьютерного моделирования процессов ОМД Учеб. пособие / Ф.В. Гречников, И.П. Попов, А.Г. Шляпугин. Самар. гос. аэрокосм. ун-т; Самара, 2007. 97 с.
В пособии рассматриваются основные вопросы компьютерного моделирования, возникающие при решении задач обработки металлов давлением.
Учебное пособие предназначено для студентов, обучающихся по специальностям 1501 – обработка металлов давлением и 1502 – машины и технология обработки металлов давлением.
Печатаются по решению редакционно-издательского совета Самарского государственного аэрокосмического университета имени академика С.П. Королева.
Рецензенты:
доктор. техн. наук, проф. Смирнов Г.В.
канд. техн. наук, Смольников С.Д.
Содержание
Содержание 4
Введение 5
1.0 Общие сведения о компьютерном моделировании 7
1.1 Основные этапы компьютерного моделирования 7
1.2 Виды моделей 12
1.3 Формализация объектов и процессов при построении модели 16
1.4 Требования, предъявляемые к моделям 21
1.5 Общий вид математических моделей 22
1.5.1 Общий вид математических моделей 22
1.5.2 Основные этапы формализации объектов и процессов при построении математической модели 25
1.5.3 Основные подходы в математическом моделировании 27
1.5.4 Основные допущения, используемые при создании математических моделей процессов ОМД 30
1.5.5 Методы решения задач ОМД 35
Контрольные вопросы 43
Объясните понятия 43
2 Реализация метода конечных элементов в современных программных продуктах 45
2.1 Особенности современных САПР программ, применяемых для моделирования процессов ОМД 46
2.2 Последовательность действий, выполняемая при моделировании в CAE-системах, использующих МЭК. 53
2.3 Создание геометрической модели и ее дискретизация. 54
2.3.1 Создание геометрической модели 54
2.3.1.1 Каркасное моделирование 56
2.3.1.2 Ограничения каркасных моделей 56
2.3.1.3 Поверхностное моделирование 59
2.3.1.4 Основные виды поверхностей, используемые при моделировании. 60
2.3.1.5 Твердотельное моделирование 64
2.3.1.6 Понятие гибридного моделирования 65
2.4 Задание типа КЭ 67
2.5 Создание сетки КЭ (ассамблирование). 71
2.6 Задание граничных условий 74
2.7 Решение контактных задач. 77
2.8 Задание свойств материала. 79
2.8.1 Модели, описывающие упругое поведение материала 79
2.8.2 Модели, описывающие пластическое состояние материала 80
2.8.3 Модели, используемые при моделировании с помощью ЭВМ 82
2.9 Выбор параметров расчета и подготовка к расчету 84
2.10 Анализ полученных результатов 85
Контрольные вопросы 90
Заключение 94
Список используемых источников 95
Введение
Невозможно представить современное производство без широкого применения моделирования. Практически на любом этапе производства, начиная от создания эскизного проекта и заканчивая контролем качества готового издания, мы сталкиваемся с понятиями модели и моделирования.
Что же такое моделирование и в чем оно заключается? Моделирование (процесс создания модели) заключается в замене исходного объекта его “образом” моделью. Полученная модель при необходимости может быть использована при решении прямых и обратных задач.
Прямые задачи отвечают на вопрос, каков получиться результат при заданных условиях функционирования модели. В частности, какой будет зависимость изменения толщины прокатываемой ленты по ширине при изменении жесткости валков прокатного стана. Для решения такой задачи строиться математическая модель, позволяющая выразить исследуемую величину, т.е. в нашем случае зависимость, связывающая изменение толщины прокатываемой ленты от жесткости валков прокатного стана.
Обратные задачи отвечают на вопрос: как выбрать единственное решение из множества решений, получаемых с помощью принятой модели так, чтобы решение отвечало заданным условиям. Например, какой должен быть профиль валков, для того чтобы разнотолщинность ленты по ширине была минимальной. Обратные задачи называются задачами оптимизации.
Прямые задачи проще обратных, поскольку для решения обратной задачи зачастую приходиться сначала решить прямую задачу.
Решение, поставленных ранее задач, требует развития специальных методов моделирования, которые бурно развиваются, охватывая все новые сферы этой области науки. Степень использования моделирования в производственном процессе говорит об уровне самого производства. Там где большую часть подготовки к производству занимает исследование и изучение процессов производства там и следует ожидать более высокое качество изготавливаемого изделия. Соответственно и требования к инженерам, обеспечивающим проектирование подобных технологических процессов предъявляться более высокие.
На современном этапе развития науки процесс моделирования очень тесно связан с использованием ЭВМ. Это объясняется рядом причин, среди которых можно выделить следующие:
большое количество повторяющихся действий выполняемых исследователем, например, при моделировании процесса штамповки поковки зубчатого колеса из цилиндрической заготовки для определения деформации с помощью метода конечных элементов необходимо выполнить сотни, тысячи одинаковых операций;
простота представления для ЭВМ большинства математических методов, используемых в моделировании;
возможность получения и представления результатов моделирования в наиболее полном и наглядном для исследователя виде. Представление результатов на компьютере, как правило, гораздо шире, чем при постановке физического эксперимента;
возможность глубокого и всестороннего изучения моделируемого объекта или процесса производства без существенных материальных затрат в сравнении с физическими экспериментами. В условиях компьютерного моделирования фактически регламентируется только время работы над проектом.
1.0 Общие сведения о компьютерном моделировании
1.1 Основные этапы компьютерного моделирования
На современном этапе развития науки и техники моделирование очень тесно связано с использованием ЭВМ, а возможности компьютерного моделирования иногда кажутся, настолько большими, что моделирование называют “третьим методом” познания, сочетающим в себе достоинства как теории так эксперимента /1/.
Компьютерное моделирование условно можно разделить на две группы: во-первых, это моделирование, в котором использованы имеющиеся программное обеспечение и, во-вторых – “классическое” – в котором созданы новые программные продукты. В соответствии с целями моделирования разработка программы может осуществляться как для конкретного технологического процесса, так и для целой группы технологических процессов или даже способов. Например, к первой группе можно отнести задачу расчета деформации валков прокатного стана заданной модели для прокатки полосы толщиной 10 мм из технически чистого алюминия. Ко второй – задачу описания всех известных способов прокатки.
В “классическом” варианте моделирования какого-либо объекта или процесса можно условно выделить следующие этапы /1/:
создание формализованной (математической) модели,
создание алгоритма,
создание программы,
отладка полученной программы.
На первом этапе собирается информация об исходном объекте, которая позволяет получить важные предварительные данные об объекте. На этом этапе возможно исследование математической модели (или ее частей) теоретическими методами. Осуществляется формализация (математическое описание исходных данных).
На втором этапе осуществляется разработка алгоритма для реализации модели на компьютере. Обычно для задач ОМД на этом этапе осуществляется представление модели в форме, удобной для применения численных методов, определяется последовательность вычислительных и логических операций, которые нужно произвести, чтобы найти искомые величины с заданной точностью.
Из требований, предъявляемых к вычислительным алгоритмам, можно выделить следующие:
- алгоритмы не должны искажать основные свойства модели и, следовательно, исходного объекта;
- алгоритмы должны быть экономичными как с точки зрения осуществления расчетов при моделировании, так и с точки зрения построения;
- алгоритмы должны быть адаптирующимися к особенностям решаемых задач, используемому языку программирования и используемым компьютерам.
На третьем этапе создаются программы, “переводящие” алгоритм на доступный компьютеру язык. К этим программам также предъявляются требования экономичности и адаптивности. При этом под экономичностью использования языка программирования понимается возможность быстро и четко описать необходимый алгоритм, а под адаптивностью – способность легко исправить или подкорректировать уже созданную программу. Полученная в результате программа становиться “электронным” эквивалентом изучаемого объекта или процесса, который в дальнейшем можно изучать на компьютере.
Как правило, для программирования используются языки высокого уровня (например, Паскаль, Бейсик и др.), поскольку их использование позволяет написать программу более качественно и быстро. Существуют также специализированные языки программирования, предназначенные для решения конкретных задач моделирования.
С помощью полученной программы, осуществляется постановка “пробных” вычислительных экспериментов и отладка системы “формализованная модель–алгоритм–программа” для достижения требуемой адекватности. После чего исследователь получает универсальный, гибкий и недорогой инструмент, позволяющий проводить разнообразные и подробные “опыты”, дающие все требуемые качественные и количественные характеристики объекта.
Рассмотрим случай “классической” постановки прямого моделирования на примере процесса обтяжки /19/. Процесс обтяжки осуществляется следующим образом: изогнутая заготовка, уложенная на пуансон и закрепленная в зажимах, деформируется под действием поднимающегося вверх пуансона (рисунок 1).
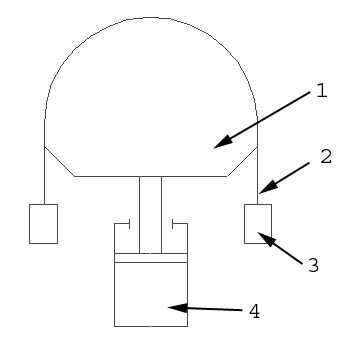
Рисунок 1 – Схема процесса обтяжки: 1 – пуансон, 2 – листовая заготовка, 3 – неподвижный зажим, 4 – гидравлический цилиндр, приводящий в движение пуансон
Замкнутого аналитического решения данной задачи, например, с учётом сдвиговых деформаций, в том числе и по толщине, не существует. Использование метода конечных элементов (МКЭ) с объёмными конечными элементами для описания геометрии листа с помощью дискретной модели усложняется из-за большого различия в размерах заготовки в направлении толщины и плоскости листа. Для описания такого тела потребуется большое количество конечных элементов и время, потраченное на расчеты процесса листовой штамповки в программах, описывающих объемное напряженное состояние, не всегда оправдано. Программ, способных осуществить расчёт обтяжки с помощью МКЭ, нет.
Поэтому при постановке задачи компьютерного моделирования в этом случае есть смысл осуществить полную разработку модели от подготовки математических данных о процессе до реализации расчета с конкретными данными технологического процесса в уже созданной программе. В других случаях, например, для описания конкретного технологического процесса вытяжки, решение которого может быть осуществлено в уже существующей программе, гораздо целесообразнее использовать уже имеющиеся программные продукты (например, программу Autoform).
Тогда “классический” вариант моделирования технологического процесса обтяжки будет состоять из следующих этапов:
Во-первых, необходимо разработать математическую модель процесса, для реализации используемого способа. В случае, если способ является новым, и математической модели не существует, то необходимо осуществить соответствующие теоретические и экспериментальные выкладки, для ее создания и подтверждения адекватности. Для осуществления расчетов с помощью метода конечных элементов модель должна быть представлена в виде уравнения описывающего в матричном виде энергетическое состояние системы.
На втором этапе последовательность расчетов, выполняемая в процессе моделирования, должна быть записана согласно требованиям ГОСТ в виде алгоритма. Для этого сначала необходимо четко определить последовательность выполнения операций.
На третьем этапе осуществляется написание программы и ее трансляция в машинный язык, используемый на ЭВМ. Если создаваемая программа сложна, то её написание может быть изначально осуществлено на бумаге. После написания программы осуществляется ее трансляция в машинный язык, работу с которым ЭВМ осуществляет гораздо быстрее, чем с любым языком программирования высокого уровня.
После получения программы осуществляется проверка данных, полученных из вычислительного эксперимента и их сравнение с экспериментальными данными, полученными в процессе обтяжки с заданными технологическими параметрами. В случае получения адекватного результата программу можно использовать для моделирования процесса с различными технологическими параметрами.
В настоящий момент для моделирования процессов ОМД прибегать к созданию программы приходиться достаточно редко, поскольку первые два этапа описанные выше уже реализованы в большом количестве существующих программных продуктов. В этом случае при создании модели достаточно лишь задать значения технологических параметров в уже существующей программе. А для случая, когда моделируемый процесс все же не укладываются в рамки используемого в программе алгоритма решения задач, в современных программах предусматривается возможность использования языков программирования для написания новых алгоритмов расчета (в программе Ansys например используется язык APDL).