Р о з д і л 2

РЯДИ

Ч а с т и н а 6

Числові ряди

6.1. Означення числового ряду та його збіжності Вираз ,

де – послідовність дійсних чисел, для якої кожний доданок визначається як функція від його номера, називається числовим рядом.

Позначають n-ну часткову суму ряду та суму ряду , при цьому a_n n-й член ряду.

Якщо , то ряд називається збіжним, якщо границя не існує, то ряд називається розбіжним.

Для збіжного ряду величину називають залишковим рядом, або залишковою сумою. Якщо ряд є збіжним, то залишковий ряд є також збіжним, тому що

.

Оскільки визначення суми ряду в більшості випадків є складним завданням, то основним питанням в теорії рядів є визначення збіжності чи розбіжності ряду, який розглядається, тобто встановлення факту, існує чи ні сума такого ряду. Якщо буде встановлено, що сума ряду, який розглядається, існує, то її за необхідності визначають, а якщо буде установлено, що ряд, який розглядається, є розбіжним, то тим самим установлюється, що його сума не існує, а отже, визначення суми такого ряду не відповідає здоровому глузду.

6.2. Ознаки збіжності числових рядів

Розглянемо відомий ряд – нескінченну геометричну прогресію

,

де , тобто .

Відомо, що такий ряд збігається, оскільки

.

Якщо , тобто , то визначений вище ряд є розбіжним, тому що

.

Для розглянутого ряду та

Розглянемо наступний ряд . Для цього ряду

, при p > 0,

але він є збіжним при p > 1 та розбіжним при 0 < p 1.

Визначений ряд при р = 1, тобто називається гармонічним рядом.

На прикладі розгляду рядів та видно, що ознака є лише необхідною ознакою збіжності ряду, але не достатньою, а ознака є достатньою ознакою розбіжності числового ряду.

Якщо для будь-якого числового ряду, члени якого є невід’ємними, установлено, що , то для твердження щодо його збіжності чи розбіжності необхідно розглянути достатні ознаки.

Ознака порівняння рядів

Якщо для будь-якого збіжного числового ряду з невід’ємними членами установлено, що всі його члени, принаймні починаючи з деякого номера, перевищують значення відповідних членів ряду, який досліджується на збіжність, то він є також збіжним рядом.

Якщо для числового ряду з невід’ємними членами, який досліджується на збіжність, установлено, що всі його члени, починаючи с деякого номера, є не меншими за відповідні члени числового ряду з невід’ємними членами, який є розбіжним рядом, то ряд, який досліджується, є також розбіжним рядом.

Задача 6.1. Установити, збігається чи ні ряд .

Розв’язання. Як ряд порівняння виберемо ряд , який збігається, тому що це нескінченна геометрична прогресія вигляду 1+q+q²+q³+… із знаменником . Видно, що , а це означає, що ряд також збігається.

Задача 6.2. Установити, збігається чи ні ряд .

Розв’язання. Для порівняння членів заданого ряду розглянемо гармонічний ряд , який є розбіжним. Видно, що при . А це означає, що ряд є також розбіжним, хоча необхідна умова збіжності виконується, оскільки .

Ознака Даламбера

Якщо для будь-якого числового ряду з невід’ємними членами, починаючи з деякого номера, границя відношення наступного члена до попереднього при не перевищує деяке невід’ємне число q < 1, тобто якщо , то такий числовий ряд збігається; в противному разі, коли q > 1 ряд розбігається; якщо q = 1, то ознака Даламбера щодо збіжності чи розбіжності відповіді не дає.

Задача 6.3. Установити збіжність ряду .

Розв’язання. Зазначимо, що необхідна ознака збіжності цього ряду виконується, оскільки

.

За достатньою ознакою Даламбера маємо

.

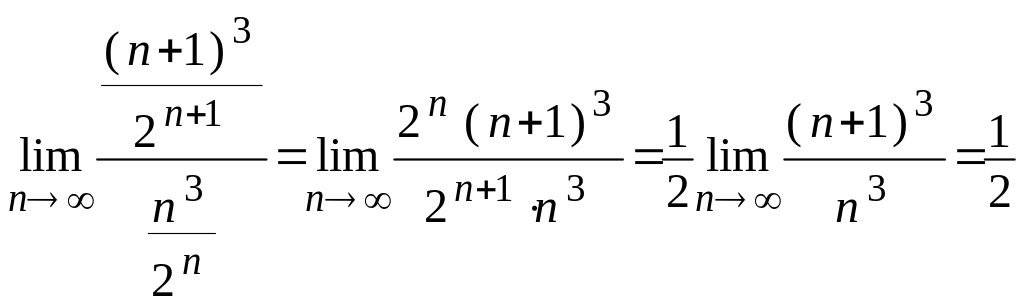Це свідчить про те, що за ознакою Даламбера слід робити висновок про те, що ряд є збіжним рядом.

Задача 6.4. Установити, збігається чи ні ряд .

Розв’язання. За достатньою ознакою Даламбера маємо

,

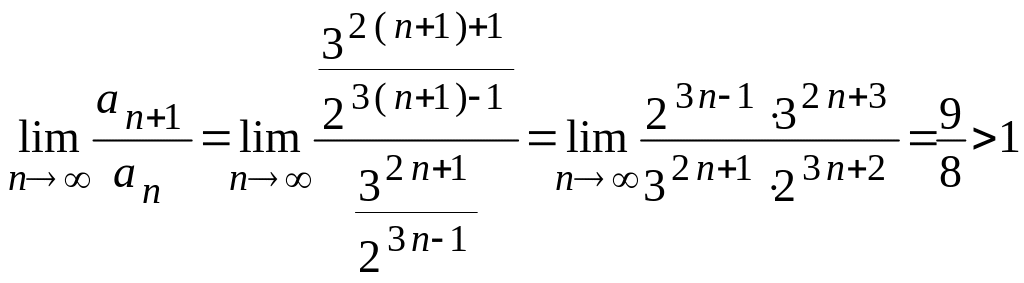тобто зазначений ряд є розбіжним.

Задача 6.5. Установити, збігається чи ні ряд .

Розв’язання. За достатньою ознакою Даламбера маємо

,

тобто зазначений для розгляду ряд розбігається.

Ознака Коші

Якщо для будь-якого числового ряду з невід’ємними членами, починаючи з деякого номера, , де q < 1, то ряд збігається, якщо , де , то ряд розбігається.

Задача 6.6. Установити, збігається чи ні ряд .

Розв’язання. Розглянемо необхідну ознаку збіжності цього ряду. Маємо

,

тобто необхідна ознака збіжності ряду виконується.

За достатньою ознакою Коші маємо

,

що означає, що ряд збігається.

Задача 6.7. Установити, збігається чи ні ряд .

Розв’язання. Розглянемо необхідну ознаку збіжності.

Будемо мати

.

За достатньою ознакою Коші маємо

,

тобто ; отже, ряд, який розглядається, є збіжним.

Інтегральна ознака Коші

Якщо у відповідність до числового невід’ємного ряду поставлена функція f(x), яка визначена при всіх , є невід’ємною та спадною, то ряд збігається тоді й тільки тоді, коли збігається інтеграл .

Задача 6.8. Установити, збігається чи ні ряд .

Розв’язання. Відзначимо, що необхідна ознака збіжності виконується, оскільки . За інтервальною ознакою Коші маємо

,

а це означає, що ряд збігається.

Задача 6.9. Установити, збігається чи ні ряд .

Розв’язання. Необхідна ознака збіжності виконується, тому що . За інтервальною ознакою Коші маємо

.

Отже ряд є розбіжним рядом.

До основних властивостей рядів, які збігаються, відносять такі.

Якщо ряд збігається, то ряд , де – дійсне число, також збігається.

Якщо кожний з рядів та збігається, то ряди також збігаються.

Якщо один з рядів та розбігається, то ряди розбігаються.

Ч а с т и н а 7