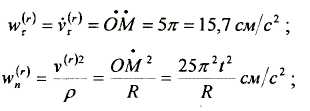3. Обчислимо відносну швидкість та відносне прискорення точки:

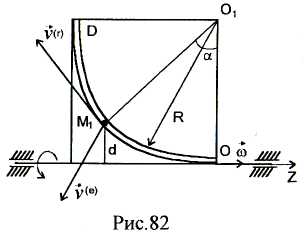
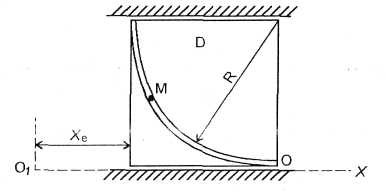
Рис.127

Знак у позитивний, тому відносна швидкість спрямована по дотичній до траєкторії в точці М1 в бік зростання дугової координати. Відносне прискорення точки дорівнює Обчислимо

^{Зобразимо на рисунку вектори}

Позитивний знак вказує на те, що спрямований в бік зростання дугової координати (рис. 127).

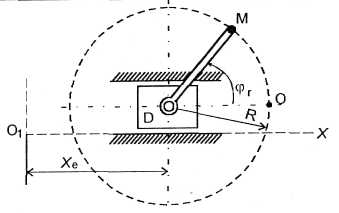
4. Визначимо переносну швидкість та переносне прискорення точки М. Переносне середовище обертається навколо нерухомої осі з кутовою швидкістю та кутовим прискоренням тому

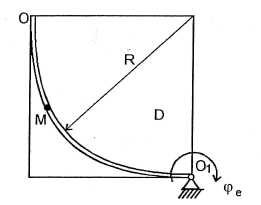
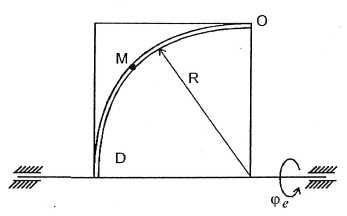
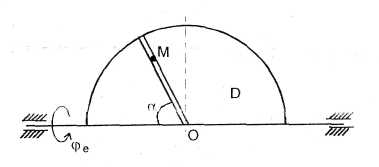
Рис. 128

d - відстань від точки до осі обертання (рис. 128), Тоді

Зобразимо вектори

Вектори та _{перпендикулярні площині креслення та обидва} спрямовані до спостерігача, тому що напрямки та співпадають. Доосьове прискорення спрямоване до осі обертання тіла D.

5. Обчислимо коріолісове прискорення :

Вектори розташовані в площині креслення, тому спрямоване перпендикулярно площині креслення до спостерігача.

Знаходимо величину коріолісова прискорення:

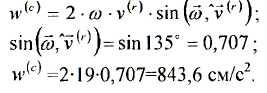
Рис. 129	Вар. 1
Рис. 130	Вар. 2
Рис. 131	Вар. 3
Рис. 132	Вар. 4
Рис.133	Вар. 5
Рис. 134	Вар. 6
Рис. 135	Вар. 7
Рис. 136	Вар. 8
Рис.137	Вар. 9
Рис. 138	Вар. 10
Рис. 139	Вар. 11
Рис. 140	Вар. 12
Рис. 141	Вар. 13
Рис.142	Вар. 14
Рис.143	Вар. 15
Рис. 144	Вар. 16
Рис.145	Вар. 17
Рис. 146	Вар. 18
Рис. 147	Вар. 19
Рис. 148	Вар. 20
Рис. 149	Вар. 21
Рис. 150	Вар. 22
Рис. 151	Вар. 23
Рис. 152	Вар. 24
Рис. 153	Вар. 25
Рис. 154	Вар. 26
Рис. 155	Вар. 27
Рис. 156	Вар. 28
Рис. 157	Вар. 29
Рис. 158	Вар. 30

6. Визначимо абсолютну швидкість та абсолютне прискорення точки.

С користаємось теоремами про складання швидкостей та прискорень:

^{Вектори перпендикулярні, тому величину абсолютної швидкості можна обчислити так:}

Абсолютна швидкість спрямована за діагоналлю прямокутника, побудованого на векторах

Для обчислення величини абсолютного прискорення точки застосуємо метод проекцій. Для цього проведемо осі х та у: вісь х вздовж сторони 00₁, а вісь у спрямована перпендикулярно площині креслення в бік спостерігача (рис. 128). Запишемо у вигляді

та будемо проектувати обидві частини цього векторного рівняння на осі х, у,

Величина абсолютного прискорення дорівнює:

У випадку, коли вектори не перпендикулярні, для знаходження величини абсолютної швидкості теж зручно користуватися методом проекцій.