Розділ 1 Кінематика

Задача 1. За заданими рівняннями руху точки М встановити вид її траєкторії та для часу t=t,(c) знайти положення точки на траєкторії, 'пі швидкість, повне, дотичне та нормальне прискорення, а також радіус кривизн ни траєкторії у відповідній точці (табл. 1)

П риклад виконання задачі 1.

Вихідні дані:

1. Визначаємо траєкторію та положення точки на траєкторії на момент часу t₁. Для того, щоб одержати рівняння траєкторії точки в формі залежності між координатами, треба виключити параметр t з рівняння, руху. З першого рівняння руху точки визначимо:

П ісля підстановки до другого рівняння одержимо:

Рис.1

Ц е рівняння параболи. Аналізуючи рівняння руху точки, робимо висновок, що траєкторією точки буде та гілка параболи, для якої значення координати х — додатне. В деяких варіантах задачі при визначенні, траєкторії або для спрощення подальших розрахунків треба врахувати відомі з тригонометрії формули:

Для знаходження положення точки на траєкторії обчислимо зна-

чения її координат на момент часу t₁ =0,5с.

х₁ = 2см ; у₁ = Зсм . Накреслимо траєкторію точки та її положення на момент часу t₁ (рис. І).

2. Визначаємо швидкість точки.

Знаходимо проекції швидкості на осі координат:

.

Величина швидкості точки дорівнює

При t=t₁ V₁ =16,5 см/с.

Для визначення напрямку швидкості обчислимо спрямовуючі косинуси :

_{Зображаємо на рисунку швидкість точки}

3. Визначаємо прискорення точки. Знаходимо проекції прискорення

точки на осі координат:

; _.

Величина прискорення дорівнює

, на будь–який час.

Обмислимо спрямовуючі косинуси:

Таблиця 1

№ вар.	Р і в н я н н я р у х у		t, с
	, см	, см
1	2	3	4
1.
2.			0,5
3.			1
4.	x = 10t	y = 4,9t2	2
5.
6.	x = 20t	y = 245-4gt2	4
7.
8.			1,5
9.
10.			1
11.
12.			1
13.
14.			0,5
15.			1
16.			2
17.
18.			1,5
19.			2
20.

Закінчення таблиці 1

1	2	3	4
21.
22.			1
23.			1
24.			1
25.			3
26.			1
27.			0,5
28.			1
29.			0,5
30.			1

4. Визначення .

Дотичне прискорення точки дорівнює

При см/с².

Тоді нормальне прискорення точки

см/с².

На рисунку зображаємо дотичне та нормальне прискорення. Радіус кривизни траєкторії визначаємо з формули для нормального прискорення .

При см.

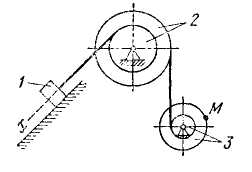
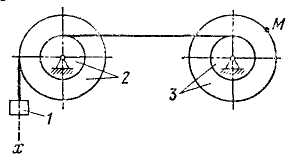
Задача 2. За поданими рівняннями прямолінійного поступального руху вантажу 1 х=х(t) визначити швидкість, обертальне, доосьове та повне прискорення точки М механізму в той час, коли шлях, який пройшов вантаж, дорівнює S. Координата х в сантиметрах, час t - у секундах (рис.2–31).

Приклад виконання задачі 2.

Дана схема механізму (рис.32).

Вихідні дані:

.

1. Визначаємо той момент часу τ, коли шлях, який пройшов вантаж А, дорівнює 40см.

^Тоді

2. Знайдемо кутові швидкості та кутові прискорення 2-ї та 3-ї ланки механізму. Величина швидкості вантажу 1

см/с.

Тому, що нитка нерозтяжна, величина швидкості вантажу 1 дорівнює величині швидкості точки А, тобто см/с.

Величина кутової швидкості 2-ї ланки механізму дорівнює

Знаходимо величину кутової швидкості 3-ї ланки із співвідношення

^звідки

Величина кутового прискорення дорівнює

Кутова швидкість та кутове прискорення колеса 3 спрямовані вздовж осі обертання за креслення.

Рис.2	Вар.
	1
Рис.3	2
Рис.4	3
Рис. 5	4
Рис. 6	Вар.
	5
Рис. 7	6
Рис. 8	7
Рис. 9	8
Рис. 10	Вар.
	9
Рис.11	10
Рис. 12	11
Рис. 13	12
Рис. 14	Вар.
	13
Рис. 15	14
Рис.16	15
Рис. 17	16
Рис.18	Вар.
	17
Рис.19	18
Рис. 20	19
Рис. 21	20
Рис. 22	Вар.
	21
Рис. 23	22
Рис. 24	23
Рис. 25	24
Рис. 26	Вар.
	25
Рис. 27	26
Рис. 28	27
Рис. 29	28
Рис. 30	Вар.
	29
Рис. 31	30

3. Знаходимо величини швидкості, обертального, доосьового та повного скорень точки М.

Величина швидкості точки М дорівнює

Швидкість спрямована перпендикулярно до радіусу в бік обертання колеса 3 (рис. 132). Величина обертального прискорення дорівнює

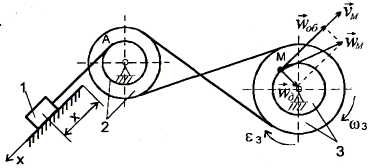
Рис. 32

Спрямоване обертальне прискорення так само, як і швидкість, тобто колесо 3 обертається прискорено. Величина доосьового прискорення точки М дорівнює

^{Спрямоване по радіусу кола до його центру.}

Величина повного прискорення дорівнює

На рисунку зображаємо швидкість та прискорення точки М.

Задача 3. У механізмах, наведених на рис.34 - 63, визначити швидкості всіх позначених точок, а також кутові швидкості всіх ланок, вважаючи, що всі відстані та означені на рисунках швидкості відомі.

Рис.33

Приклад виконання задачі 3.

Дана схема механізму (рис. 33)

Вихідні дані: кутова швидкість ланки 1 - кривошипа О А;

геометрія креслення.

1. Ланка 1 - кривошип ОА.

Кривошип обертається навколо нерухомої осі, що проходить через точку О перпендикулярно до площини креслення. Тому величина швидкості точки А дорівнює

та спрямована перпендикулярно ОА, як показано на кресленні (рис.33).

2. Розглянемо ланку 2 - колесо.

Колесо здійснює плоскопаралельний рух. Для того, щоб визначити швидкість будь-якої точки колеса та його кутову швидкість, необхідно побу­дувати миттєвий центр швидкостей. Оскільки колесо котиться без ковзання по нерухомій поверхні, миттєвий центр швидкостей знаходиться в точці дотику колеса та поверхні. Позначимо цю точку M₂. Використовуючи те, що величини швидкостей точок пропорційні відстаням від точок до миттєвого центру швидкостей, запишемо співвідношення

^звідки

Спрямована швидкість точки В перпендикулярно відрізку, що з'єднує точку з МЦШ, в бік обертання тіла (рис. 33).

Щоб визначити величину кутової швидкості тіла, треба величину швидкості будь-якої точки тіла розділити на її відстань до МЦШ:

Покажемо на кресленні вектор (рис.33).

3. Ланка 3 - шатун BD.

Шатун здійснює плоскопаралельний рух. Відомі величина та напрямок швидкості точки В та напрямок швидкості точки D, бо точка D одночасно належить і повзуну, який може рухатись вздовж вертикальних спрямовуючих.

Оскільки швидкості паралельні, але не перпендикулярні

відрізку, який їх з'єднує, миттєвий центр швидкостей знаходиться у нескінченності. В цьому випадку шатун здійснює миттєво-поступальний рух, тому

4. Ланка 4 - шатун CF.

Шатун здійснює плоскопаралельний рух. Відомі величина та напрямок швидкості точки С та напрямок швидкості точки F. (Точка F належить і повзуну, що рухається вздовж горизонтальних спрямовуючих).

Для даного положення механізму миттєвий центр швидкостей буде знаходитись в точці F, тому що перпендикуляри до швидкостей

перетинаються у точці F. Виходячи з цього

Т оді

звідки

Напрямки зображені на кресленні (рис. 33).

Рис.34			Рис.35
Рис.36			Рис.37
Рис.38		Рис.39
Рис.40		Рис.41
Рис.42		Рис.43
Рис.44		Рис.45
Рис.46		Рис.47
Рис.48		Рис.49
Рис.50	Рис.51
Рис.52	Рис.53
Рис.54	Рис.55
Рис.56	Рис.57
Рис.58	Рис.59
Рис.60	Рис.61

Рис.62

Рис.63

5. Ланка 5 - шатун EL.

Шатун EL здійснює плоскопаралельний рух. Відомі величина та напрямок швидкості точки Е та напрямок швидкості точки L, бо точка L належить одночасно і кривошипу KL, а отже швидкість спрямована вздовж перпендикуляра до KL. Побудуємо перпендикуляри до швидкостей та .Точка перетину – М₅,миттєвий центр швидкостей ланки 5.

^Тоді

^звідки

^{Напрямки зображені на кресленні (рис. 33).}

6. Ланка 6 - кривошип KL.

Кривошип обертається навколо нерухомої осі, що проходить через точ-

ку К перпендикулярно до площини креслення. Величина і напрямок v _L нам вже відомі, тому

^{Напрямок показаний на кресленні (рис.33).}

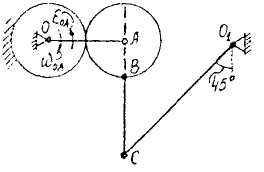
Задача 4. Для заданого положення механізму знайти швидкості точок А, В, С та кутові швидкості всіх ланок механізму, якщо відома кутова швидкість кривошипа _ОА (рис.65-94).

Приклад виконання задачі 4.

Дана схема механізму (рис.64).

Вихідні дані: ОА=40см; АВ=80см; ВС=25см; г=15см; едм=2 с-¹.

1. Визначаємо швидкість точки А. Величина швидкості дорівнює

_{Швидкість}

^{спрямована перпендикулярно до кривошипа О А.}

2. Ланка АВ здійснює плоскопаралельний рух. Для визначення швидкості точки В побудуємо миттєвий центр швидкостей ланки АВ. Швидкість точки В спрямована горизонтально. Побудуємо перпендикуляри до швидкостей точок А та В у цих точках, знайдемо точку перетину цих перпендикулярів – М₁. Це і буде миттєвий центр швидкостей ланки АВ. Якщо використаємо властивість величин швидкостей тіла при плоскопаралельному русі знайдемо v_В

,

звідки

.

Знайдемо відрізки АМ₁ та ВМ₁:

Таким чином,

Обчислимо v_В :

^{Спрямована швидкість по горизонталі ліворуч (рис.64). Кутова}

^{швидкість ланки АВ дорівнює:}

та спрямована перпендикулярно площині креслення від спостерігача.

Рис.64

4. Знайдемо швидкість точки С , що належить колесу. Колесо здійснює плоскопаралельний рух та котиться без ковзання., тому миттєвий центр швидкостей колеса знаходиться в точці дотику колеса та нерухомої поверхні – точці М₂.

Тоді

^звідки .

СМ₂ знаходимо за теоремою косинусів:

Тоді

Рис.65	Вар. 1
Рис. 66	Вар. 2
Рис.67	Вар. 3
Рис.68	Вар. 4
Рис.69	Вар. 5
Рис.70	Вар. 6
Рис.71	Вар. 7
Рис. 72	Вар. 8
Рис.73	Вар. 9
Рис.74	Вар. 10
Рис.75	Вар. 11
Рис. 76	Вар. 12
Рис.77	Вар. 13
Рис.78	Вар. 14
Рис.79	Вар. 15
Рис.80	Вар 16
Рис.81	Вар. 17
Рис.82	Вар. 18
Рис.83	Вар. 19
Рис.84	Вар. 20
Рис.85	Вар. 21
Рис.86	Вар. 22
Рис.87	Вар. 23
Рис.88	Вар. 24
Рис.89	Вар. 25
Рис.90	Вар. 26
Рис.91	Вар. 27
Рис.92	Вар. 28
Рис.93	Вар. 29
Рис.94	Вар. 30

^{Спрямована швидкість перпендикулярно відрізку СМ}₂^{, як показано} на рис.64.

Кутова швидкість колеса дорівнює

і спрямована перпендикулярно площині креслення до спостерігача (рис.64).

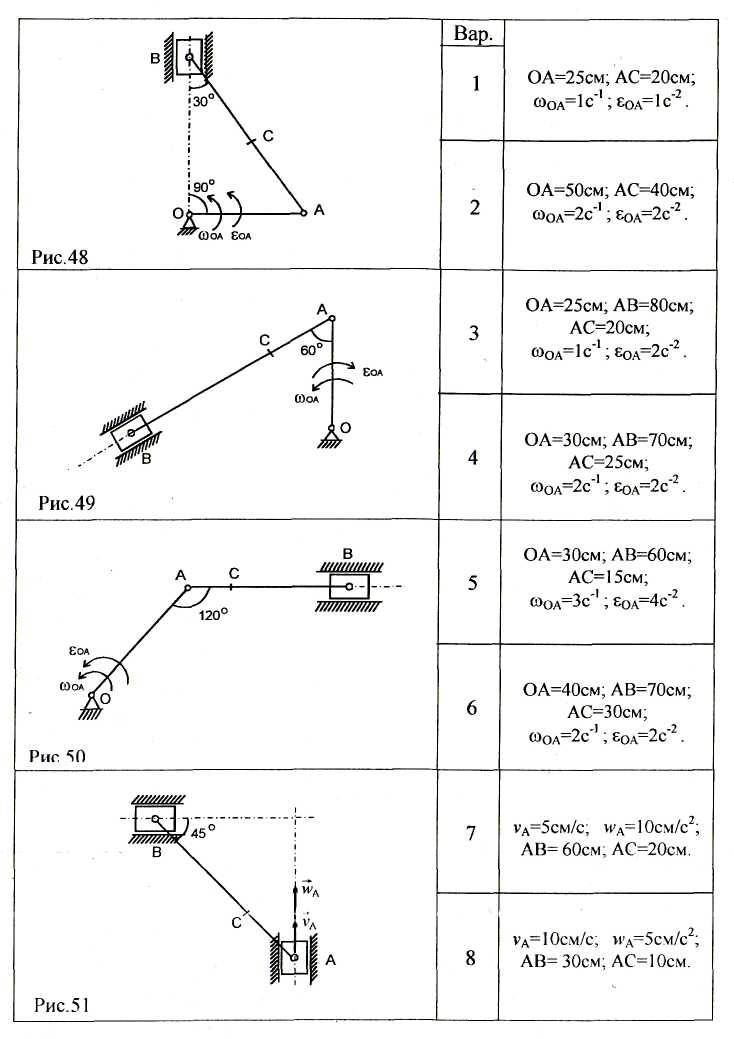
Задача 5. Для заданого положення механізму знайти швидкості та прискорення точок В та С (рис.96–62).

Приклад виконання задачі 5.

Дана схема механізму (рис.95).

Вихідні дані: 0А=10см; АВ=60 см; АС = 20 см; со _0А= 1,5 с^-1;ε_Оа=2 с^-2_.

1. Визначаємо швидкості точок А, В, С.Величина швидкості точки А

дорівнює

^{Ш видкість спрямована перпендикулярно до} кривошипа ОА, як по­казано на кресленні (рис.95).

Ланка АВ здійснює плоско-паралельний рух, тому для знаходження швидкостей точок В та С потрібно побудувати миттєвий центр швидкостей.

Побудуємо перпендикуляри до швидко­стей точок А та В у цих точках, знайдемо точку М - миттєвий центр швидкостей ланки АВ. Ве­личини швидкостей точок В та С визначаються з співвідношень

Р ис. 95 ^Звідки

Знаходимо AM, BMта CM:

Отже, величини швидкостей дорівнюють

^{Вектори спрямовані відповідно перпендикулярно ВМ та CM і}

орієнтовані так само, як вектор v_A .

Кутова швидкість тіла АВ спрямована перпендикулярно площині креслення від спостерігача, а її величина дорівнює

2. Визначаємо прискорення точок А, В, С.

Рис. 96	Вар. 1
Рис. 97	Вар. 2
Рис. 98	Вар. 3
Рис. 99	Вар. 4
Рис. 100	Вар. 5
Рис. 101	Вар. 6
Рис. 102	Вар. 7
Рис. 103	Вар. 8
Рис. 104	Вар. 9
Рис. 105	Вар. 10
Рис. 106	Вар. 11
Рис. 107	Вар. 12
Рис. 108	Вар. 13
Рис. 109	Вар. 14
Рис. 110	Вар. 15
Рис. 111	Вар. 16
Рис.112	Вар. 17
Рис. 113	Вар. 18
Рис. 114	Вар. 19
Рис. 115	Вар. 20
Рис. 116	Вар. 21
Рис.117	Вар. 22
Рис. 118	Вар. 23
Рис. 119	Вар. 24
Рис. 120	Вар. 25
Рис. 121	Вар. 26
Рис.122	Вар. 27
Рис. 123	Вар. 28
Рис. 124	Вар. 29
Рис. 125	Вар. 30

Прискорення точки А складається з обертального та доосьового прискорень:

^{Вектор спрямований перпендикулярно до кривошипа ОА в бік, протилежний швидкості, тому що кривошип ОА обертається уповільнено} (рис.126).

^{Вектор спрямований від точки А до О.}

Тіло АВ здійснює плоскопаралельний рух. Обравши полюс в точці А, на підставі формули Рівальса виразимо прискорення точки В:

або (5.1)

Величина доосьового прискорення точки В дорівнює:

^{Вектор спрямований по прямій АВ від точки В до} полюса А (рис.126).

Величина обертального прискорення точки В невідома, тому що кутове прискорення невідоме. Що ж стосується напрямку то цей вектор перпендикулярний до АВ. Будемо вважати, що спрямоване так, як показано на рис.126. Точка В ланки АВ одночасно належить і повзуну, який може рухатись вертикально. Отже, вектор спрямований по вертикалі. Будемо вважати, що спрямоване вниз. В точці В побудуємо вектори оберемо осі координат, як показано на рис.126, та спроектуємо обидві частини рівняння (5.1) на осі х та y:

Рис.126

( 5.2 ) ( 5.3 )

З рівняння (5.2) знаходимо

^{Знак « - » означає, що спрямоване вертикально вверх, а не вниз,} як ми припускали.

3 рівняння (5.3) знаходимо

^{Позитивний знак означає, що спрямоване так, як показано на} рисунку. За напрямком цього прискорення відносно полюса А визначається напрямок кутового прискорення цей вектор перпендикулярний ^{площині креслення та спрямований до спостерігача (протилежно}

Знайдемо величину

Знайдемо величину прискорення точки С:

або

^(5.4)

На рисунку в точці С будуємо Знаходимо

Відповідно до напрямку вектор спрямований перпендикулярно АС. Вектор спрямований вздовж АС від точки С до полюса А.

Проектуємо обидві частини рівняння (5.4) на осі х та у.

Величина прискорення точки С дорівнює

Задача 6. За заданим рівнянням руху тіла D та відносного руху точки М по відношенню до тіла D визначити для часу абсолютну швидкість та абсолютне прискорення точки М (рис. 129–158).

Приклад виконання задачі 6.

Дана схема механізму (рис.127).

Вихідні дані:

1. Зв'яжемо рухому систему координат з тілом D. Ця система обертається навколо нерухомої осі за законом Введемо вісь Z, спрямовану за віссю обертання в той бік, звідки відлік кута видно проти годинникової стрілки (рис. 127).

Обчислимо кутову швидкість та кутове прискорення тіла

Для часу

Позитивні знаки вказують, що спрямовані вздовж осі z в бік позитивного напрямку осі z (рис. 127).

2. Відносний рух точки відбувається за колом радіуса R за законом

_.

Знайдемо положення точки на траєкторії на момент часу

Для цього обчислимо кут між радіусами, проведеними в точки О та M_t:

На траєкторії покажемо точку М.