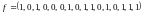- •Ф едеральное агентство по образованию фгоу спо «Астраханский государственный политехнический колледж»
- •«Элементы математической логики»
- •230103 «Автоматизированные системы обработки информации и управления»
- •230105 «Программное обеспечение вычислительной техники и автоматизированных систем» Астрахань
- •Высказывания. Операции над высказываниями
- •Формулы логики высказываний. Равносильность формул. Равносильные преобразования и упрощения формул
- •Булевы функции. Равенство булевых функций. Существенные и фиктивные переменные. Двойственность булевых функций
- •Нормальные формы булевых функций. Многочлен Жегалкина
- •Минимизация булевых функций
- •Полные системы булевых функций
Нормальные формы булевых функций. Многочлен Жегалкина
Контрольные вопросы
Дайте определение литеры.
Дайте определение конъюнкта. Какой конъюнкт называется совершенным?
Дайте определение дизъюнкта. Какой дизъюнкт называется совершенным.
Сформулируйте и докажите лемму о разложении булевой функции по переменной.
Сформулируйте и докажите теорему Шеннона.
Сформулируйте предельную теорему Шеннона.
Сформулируйте двойственную предельную теорему Шеннона.
Дайте определение литеры, элементарной конъюнкции, элементарной дизъюнкции.
Докажите лемму о разложении булевой функции по переменной
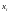 .
.Сформулируйте и докажите теорему о разложении Шеннона.
Что такое предельное разложение Шеннона, двойственное предельное разложение Шеннона?
Дайте определение ДНФ (КНФ). Сформулируйте алгоритм приведения функции к ДНФ (КНФ) посредством равносильных преобразований.
Дайте определение СКНФ (СДНФ). Приведите примеры СДНФ (СКНФ).
Сформулируйте алгоритм приведения булевой функции к СДНФ (СКНФ) посредством равносильных преобразований.
Как построить СДНФ (СКНФ) с помощью таблицы истинности булевой функции?
Дайте определение многочлена Жегалкина.
Что такое канонический многочлен Жегалкина?
Сформулируйте и докажите теорему о существовании представления булевой функции в виде многочлена Жегалкина.
Дайте определение канонического многочлена Жегалкина. Методы построения многочлена Жегалкина для булевой функции (метод равносильных преобразований, метод неопределенных коэффициентов).
Упражнения
Установите, какие из указанных функций являются ДНФ, КНФ, СДНФ и СКНФ:
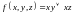 ;
;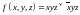 ;
; ;
;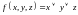 ;
;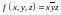 ;
;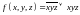 ;
;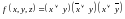 .
.
Постройте ДНФ для следующих с помощью равносильных преобразований:
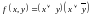 ;
;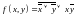 .
.
Постройте КНФ с помощью равносильных преобразований:
 ;
;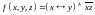 .
.
Постройте для функции
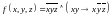 СДНФ и СКНФ с помощью равносильных
преобразований.
СДНФ и СКНФ с помощью равносильных
преобразований.Постройте СДНФ и СКНФ для функции
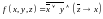 с помощью таблицы истинности.
с помощью таблицы истинности.Постройте канонический многочлен Жегалкина для функции
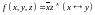 методом
элементарных преобразований.
методом
элементарных преобразований.Постройте канонический многочлен Жегалкина для функции
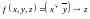 методом неопределенных коэффициентов.
методом неопределенных коэффициентов.Используя равносильные преобразования, построить ДНФ, КНФ, СДНФ и СКНФ для следующих функций:
 ;
;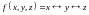 ;
;
Используя формулы разложения Шеннона, постройте СДНФ и СКНФ для следующих функций:
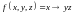 ;
;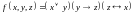 ;
;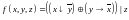
Построить ДНФ и КНФ для функции
 .
.Используя равносильные преобразования, построить СДНФ для функции
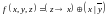
Постройте СКНФ для заданной функции, используя двойственное предельное разложение Шеннона:
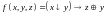 .
.
Методом равносильных преобразований найти канонический многочлен Жегалкина для функции
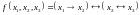
Найти канонический многочлен Жегалкина методом неопределенных коэффициентов для функции
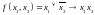 .
.
Используя равносильные преобразования, построить ДНФ, КНФ, СДНФ и СКНФ для следующих функций:
;
;
Используя формулы разложения Шеннона, постройте СДНФ и СКНФ для следующих функций:
;
;
С помощью эквивалентных преобразований постройте для функции ДНФ, КНФ, СДНФ, СКНФ.
Методом равносильных преобразований найти канонический многочлен Жегалкина:
 ;
; ;
;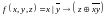 .
.
Найти канонический многочлен Жегалкина для следующих функций, используя метод неопределенных коэффициентов:
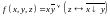 ;
; ;
;