Оглавление

ОГЛАВЛЕНИЕ 3

Введение 4

I. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ К КОНТРОЛЬНОЙ РАБОТЕ № 5 5

1. Дифференциальные уравнения 5

1.1. Общие понятия 5

1.2. Дифференциальные уравнения первого порядка 5

1.3. Решение некоторых дифференциальных уравнений второго порядка с помощью понижения порядка 9

1.4. Линейные дифференциальные уравнения 12

I. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ К КОНТРОЛЬНОЙ РАБОТЕ № 6 20

2. Ряды 20

2.1. Числовые ряды 20

2.2. Функциональные ряды 23

3. Теория вероятностЕЙ 29

3.1. Определение вероятности события А 30

3.2. Элементы комбинаторики 31

3.3. Сложные события. Теоремы сложения и умножения 34

3.4. Повторение испытаний 36

3.5. Случайные величины 39

СПИСОК РекомендуемЫХ ИСТОЧНИКОВ 43

ПриложениЯ 44

Введение

Теория дифференциальных уравнений — один из основных разделов современной математики, использующийся во многих технических и специальных дисциплинах, играющий важную роль в подготовке инженеров.

С помощью дифференциальных уравнений были открыты и объяснены электромагнитные волны, изучены различные колебательные процессы и т.д.

Ряды широко используются в приближенных вычислениях. С помощью рядов вычисляют значения функций, составляют таблицы, находят неопределенные интегралы, записывают специальные функции, вычисляют определенные интегралы, решают дифференциальные уравнения и т.д.

Теория вероятностей — сравнительно молодая наука. Возникнув в процессе решения задач игрового (азартные игры) и прикладного (страховое дело) характера, способствовала образованию и развитию новых наук: теории информации, теории надежности и др.

В методических рекомендациях содержатся краткие теоретические сведения и типовые примеры по разделам «Дифференциальные уравнения», «Ряды», «Теория вероятностей», входящие в контрольные работы № 5, 6.

В контрольной работе № 5 изучается раздел высшей математики «Дифференциальные уравнения» и рассматриваются типовые примеры.

В контрольной работе № 6 изучаются два раздела математики — «Ряды» и «Теория вероятностей» и рассматриваются типовые примеры.

Условия задач для контрольных работ № 5 и 6 даны в источнике [1]. Перед решением задач следует проработать теоретический материал по данным указаниям и по учебникам [2, 3, 5].

Методические рекомендации предназначены для студентов специальностей 190601 «Автомобили и автомобильное хозяйство», 110301 «Механизация сельского хозяйства», 110302 «Электрификация и автоматизация сельского хозяйства», 270102 «Промышленное и гражданское строительство» заочной формы обучения.

I. Методические рекомендации к контрольной работе № 5

Цель работы: изучение методов решения некоторых дифференциальных уравнений 1-го и 2-го порядков.

Литература: [2, гл. I; 3, гл. XII].

1. Дифференциальные уравнения

1.1. Общие понятия

Определение. Дифференциальным (сокращенно д.у.) называют уравнение, связывающее независимую переменную, искомую функцию и ее производные (или дифференциалы). Например, для функции у = у(х) дифференциальными будут уравнения:

, , ,

, ,

где , , …

Независимая переменная, искомая функция могут в уравнении отсутст-вовать, но наличие производных (или дифференциалов) в уравнении обяза-тельно. При этом наивысший порядок производной называют порядком д.у. Так, из приведенных выше уравнений первые три — д.у. первого порядка, четвертое — второго порядка, пятое — третьего порядка.

Определение. Решением дифференциального уравнения называют функцию, удовлетворяющую данному уравнению. Например, для уравнения решениями будут (проверьте!) функции: . Среди решений д.у. выделяют: общее, частное и особое. Решение д.у. может получаться в явном или неявном виде. В последнем случае его называют интегралом (общим, частным или особым).

Замечание. Если вместо функции одной переменной и производных (которые называют обыкновенными) в уравнение входит функция нескольких переменных и ее частные производные, то уравнение называют дифференциальным с частными производными. Например,

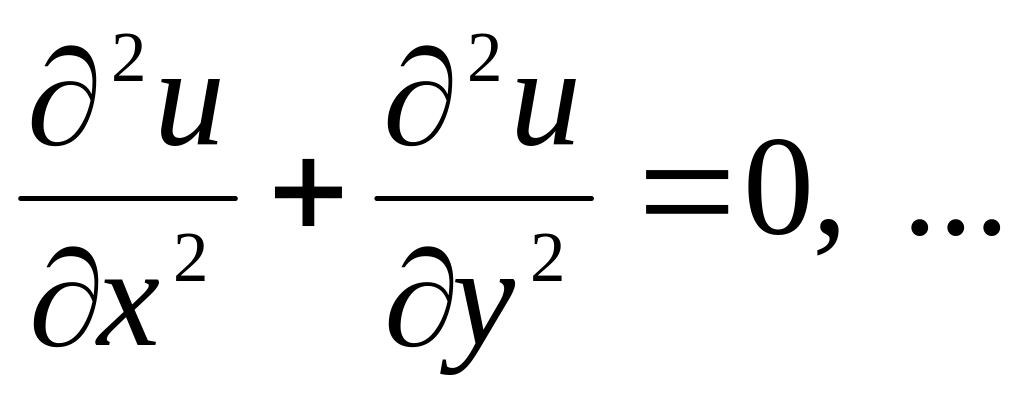
В данном издании рассматриваются только д.у. с обыкновенными производными.