2.3 Операції над нечіткими множинами

Визначення операцій, над нечіткими множинами, багато в чому аналогічно операціям над звичайними («чіткими») множинами. Допустимо, що дві нечітких множини А и В задані своїми функціями приналежності μ_А(х) і μ_В(х) (рис. 2.4. а). Тоді над цими множинами можна виконувати наступні операції.

Еквівалентність. Дві нечітких множини А і В еквівалентні (це позначається як А≡В) тоді й тільки тоді, коли для всіх х Є X має місце μ_А (х) = μ_В(x).

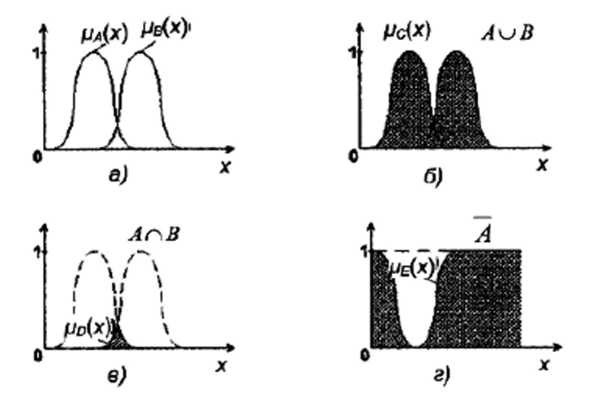
Рис. 2.4. Операції над нечіткими множинами

Включення. Нечітка множина А належить до нечіткої множини В(А В) тоді й тільки тоді, коли

μ_A(x) ≤ μ_B(x), x Є Х. (2.7)

Об'єднання, або диз'юнкція (disjunction), А В двох нечітких множин А і В відповідає логічній операції «АБО» і визначається як найменша нечітка множина, що містить обидві множини А і В. Функція приналежності для цієї множини знаходиться за допомогою операції узяття максимуму (рис. 2.4. б)

(2.8)

Перетинання, або кон’юнкція (conjunction), А В відповідає логічній операції «І» і визначається як найбільша нечітка множина, що є одночасно підмножиною обох множин. Функція приналежності множини А В виражається за допомогою операції знаходження мінімуму (рис. 2.4. в)

(2.9)

Доповнення (complement) нечіткої множини А, що позначається через (або _–А), відповідає логічному запереченню "НЕ" і визначається виразом (рис. 2.4. г)

(2.10)

Очевидно, що стосовно до класичних «чітких» множин, для яких функції приналежності приймають тільки 2 значення: 0 або 1, вираз (2.8) - (2.10) визначають відомі операції логічного «АБО», «І», «НЕ».

Приведемо визначення ще двох досить розповсюджених операцій над нечіткими множинами - алгебраїчного добутку й алгебраїчної суми нечітких множин.

Алгебраїчний добуток АВ нечітких множин А і В визначається в такий спосіб:

(2.11)

Алгебраїчне додавання А В:

(2.12)

Крім перерахованих, є й інші операції, називані іноді модифікаціями, які виявляються корисними при роботі з лінгвістичними змінними.

Операція концентрації (concentration) CON (А) визначається як алгебраїчний добуток нечіткої множини А на саму себе: CON (А) = А², т.т.

(2.13)

У результаті застосування цієї операції до множини А зменшуються ступені приналежності елементів х цієї множини, причому якщо , то це зменшення відносно мало, а для елементів з малим ступенем приналежності - відносно велико. У природній мові застосування цієї операції до того або іншого значення лінгвістичної змінної А відповідає використанню посилюючого терма «дуже» (наприклад, «дуже високий», «дуже старий» і т.д.).

Операція розтягання (dilation) DIL(A) визначається як:

DIL(A) = A^0,5. (2.14)

де

Дія цієї операції протилежна дії операції концентрації й відповідає невизначеному терму «досить», що виконує функцію ослаблення наступного за ним (основного) терма А: «досить високий», «досить старий» і т.п.

Можна ввести й інші аналогічні за змістом операції, що дозволяють модифікувати значення лінгвістичної змінної, збільшуючи в такий спосіб їх кількість. Так, терм «більш ніж» можна визначити в такий спосіб:

"більш ніж А"= , (2.15)

складений терм «дуже дуже»:

"дуже дуже А"= CON(CON(A)) = (2.16)

і т.д.