
- •Лекція 2 Тема 2 лінійні розгалужені електричні кола постійного току
- •2.1. Закони Кірхгофа
- •Питання для самоконтролю
- •2.2. Застосування законів Кірхгофа
- •2.3. Метод контурних струмів
- •Питання для самоконтролю
- •2.4. Метод вузлових потенціалів
- •Питання для самоконтролю
- •2.5. Еквівалентні перетворення
- •Питання для самоконтролю
- •2.6. Метод двох вузлів
- •Питання для самоконтролю
- •2.7. Метод активного двополюсника
- •Питання для самоконтролю
- •2.8. Принцип суперпозиції і його застосування
- •Питання для самоконтролю
- •Завдання для самоконтролю
Питання для самоконтролю
Приведіть приклад розрахункової схеми розгалуженого кола з чотирма вузлами.
Запишіть для приведеної розрахункової схеми розгалуженого кола (пункт 1) рівняння для розрахунку вузлових потенціалів і розшифруйте умовні позначення провідностей і добутків е.р.с. на провідності.
Запишіть для приведеної розрахункової схеми розгалуженого кола (пункт 1) вираз для розрахунку сил струмів, використовуючи вузлові потенціали.
2.5. Еквівалентні перетворення
схем з'єднань опорів
Розглянемо розрахункову схему кола з послідовним з'єднанням опорів (рис.2.5).
С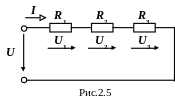 кладаємо
рівняння за 2-м законом
Кірхгофа:
кладаємо
рівняння за 2-м законом
Кірхгофа:
U = U1 + U2 + U3 ;
або
U = R1I + R2I + R3I =
= (R1 + R2 + R3)I = RеI ,
де
Rе = R1 + R2 + R3 – еквівалентний опір послідовно з'єднаних опорів.
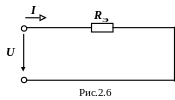 Таким
чином, задану схему з'єднання опорів
(рис.2.5) можна замінити еквівалентною
(рис.2.6). При
еквівалентному перетворенні напруга
на затисках кола і сила струму в колі
не змінюються.
Таким
чином, задану схему з'єднання опорів
(рис.2.5) можна замінити еквівалентною
(рис.2.6). При
еквівалентному перетворенні напруга
на затисках кола і сила струму в колі
не змінюються.
Розглянемо розрахункову схему кола з паралельним з'єднанням опорів (рис.2.7).
Складаємо рівняння за 1-м законом Кірхгофа:
I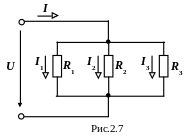 = I1
+ I2
+ I3
.
= I1
+ I2
+ I3
.
Сили струмів у розгалуженнях дорівнюють:
I1 = g1U ; I2 = g2U ; I3 = g3U .
Підставивши отримані значення в рівняння, складене за 1-м законом Кірхгофа, одержимо:
I = g1U + g2U + g3U =
= (g1 + g2 + g3)U = gеU,
де
gе = g1 + g2 + g3 – еквівалентна провідність паралельно з'єднаних опорів.
Визначаємо еквівалентний опір:
![]() ,
,
звідки
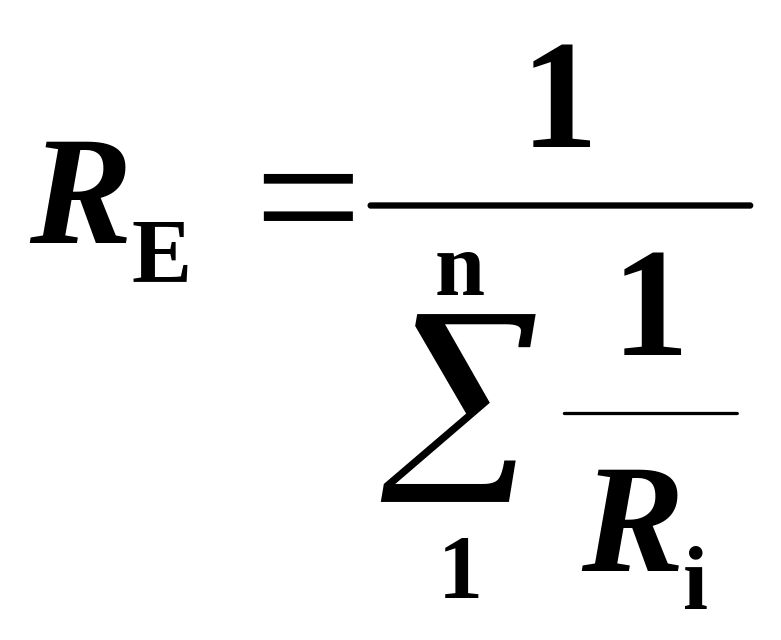 .
.
Таким чином, задану схему з'єднання опорів (рис.2.7) можна замінити еквівалентною. При еквівалентному перетворенні напруга на затисках кола і сила струму в колі не змінюються.
При розрахунках електричних кіл часто буває необхідно перетворити схему з'єднання опорів «трикутником» у «зірку» і навпаки.
Наприклад, розрахунок сил струмів у розгалуженнях найбільш раціонально виконувати на підставі схеми, приведеної на рис.2.9 (у порівнянні зі схемою, приведеної на рис.2.8).
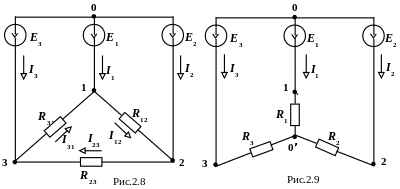
За 1-м законом Кірхгофа для вузла 0 «зірки» (рис.2.9) можемо записати:
I1 + I2 + I3 = 0,
де
I1 = (1 – 0’) g1 ; I2 = (2 – 0’) g2 ; I3 = (3 – 0’) g3 .
Підставивши ці значення сил струмів у рівняння, складене за 1-м законом Кірхгофа, одержимо:
1 g1 – 0’ g1 + 2 g2 – 0’ g2 + 3 g3 – 0’ g3 = 0 .
Визначимо потенціал вузла 0’ з отриманого рівняння:
![]() .
.
Підставивши значення 0’ у вираз для сили струму I1, одержимо:
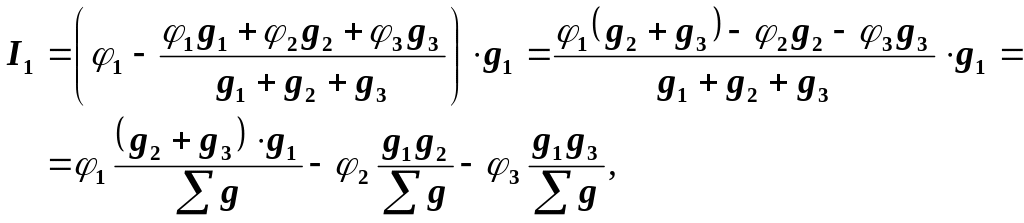
де
g = g1 + g2 + g3 .
За 1-м законом Кірхгофа для вузла 1 «трикутника» (рис.2.8) можемо записати:
I1 + I31 – I12 = 0 ,
звідки
I1 = I12 – I31 ,
де
I12 = (1 – 2) g12 ; I31 = (3 – 1) g31 .
Підставивши ці значення сил струмів у рівняння, складене за 1-м законом Кірхгофа, одержимо:
I1 = 1 (g12 + g31) – 2 g12 – 3 g31 .
При еквівалентом перетворенні схем з'єднання опорів потенціали вузлів 1, 2, 3 і сили струмів I1, I2, I3 не змінюються. Тому коефіцієнти в отриманих виразах сили струму I1 для схем з'єднання «зіркою» і «трикутником» повинні бути однаковими. Отже, можемо записати:
![]() ;
;
![]() ,
,
і за аналогією
![]() .
.
Якщо в отриманих виразах провідності замінити опорами і виконати перетворення, то одержимо вирази перетворення схеми з'єднання опорів «зіркою» в еквівалентну схему з'єднання «трикутником»:
![]() ;
;
![]() ;
;
![]() .
.
Аналогічно можна одержати вирази перетворення схеми з'єднання опорів «трикутником» в еквівалентну схему з'єднання «зіркою»:
![]() ;
;
![]() ;
;
![]() .
.
Приклад 2.3
Виконати еквівалентне перетворення схеми з'єднання опорів «трикутником» в еквівалентну схему з'єднання опорів «зіркою» на прикладі розрахункової схеми кола, приведеної на рис.2.2.
Рішення.
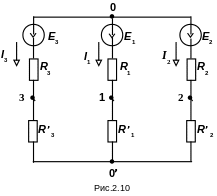 Складаємо
еквівалентну схему (рис.2.10) і визначаємо
еквівалентні опори:
Складаємо
еквівалентну схему (рис.2.10) і визначаємо
еквівалентні опори:
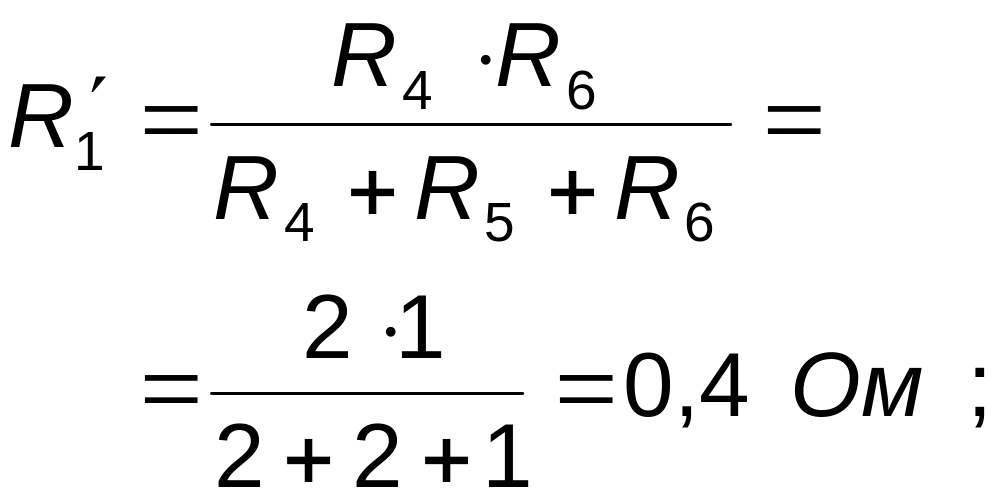
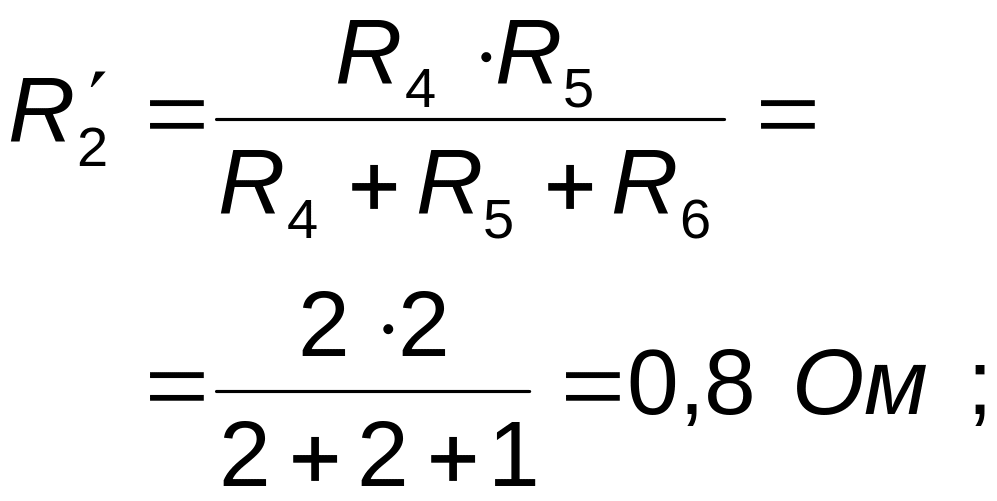
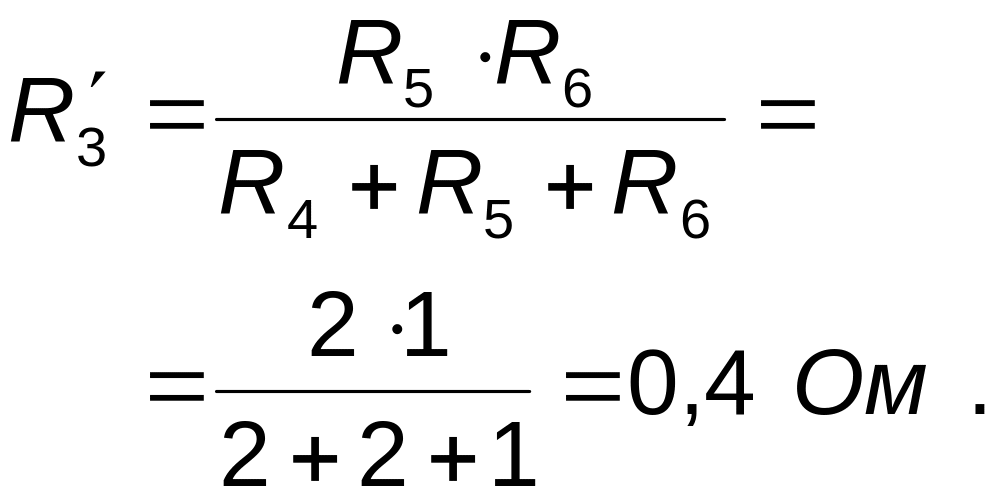
 Остаточно
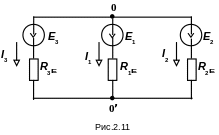
одержимо розрахункову схему, приведену
на рис.2.11, і наступні значення опорів:
Остаточно
одержимо розрахункову схему, приведену
на рис.2.11, і наступні значення опорів:
R1е = R1 + R’1 =
= 0,6 + 0,4 = 1 Ом ;
R2е = R2 + R’2 =
= 1,2 + 0,8 = 2 Ом ;
R3е = R3 + R’3 =
= 1,6 + 0,4 = 2 Ом .
