Питання для самоконтролю

1. Приведіть приклад розрахункової схеми розгалуженого кола з чотирма вузлами.

2. Позначте на приведеній розрахунковій схемі розгалуженого кола (пункт 1) умовно позитивні напрями струмів і виберите напрями контурних струмів.

3. Запишіть для приведеної розрахункової схеми розгалуженого кола (пункт 1) рівняння для розрахунку контурних струмів і розшифруйте умовні позначення повних опорів контурів, опорів суміжних розгалужень, контурних е.р.с.

4. Запишіть для приведеної розрахункової схеми розгалуженого кола (пункт 1) сили струмів у розгалуженнях через сили контурних струмів.

2.4. Метод вузлових потенціалів

Одним зі шляхів розрахунку сил струмів на ділянках кола є визначення спочатку потенціалів точок, а потім з їх допомогою напруг і сил струмів. Метод розрахунку електричних кіл, у яких невідомими приймаються потенціали вузлів схеми, називають методом вузлових потенціалів.

Р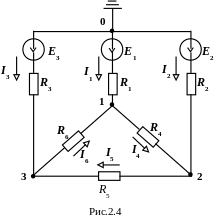 озглянемо суть цього методу, скориставшись розрахунковою схемою, представленою на рис.2.4. Потенціал вузла 0 приймаємо рівним нулю (₀ = 0).

Складаємо рівняння за 1-м законом Кірхгофа:

д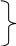 ля вузла 1: I₁ + I₆ – I₄ = 0 ;

для вузла 2: I₂ + I₄ – I₅ = 0 ;

для вузла 3: I₃ + I₅ – I₆ = 0 .

Змінимо в цих рівняннях знаки на протилежні:

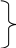–I₁ – I₆ + I₄ = 0 ;

–I₂ – I₄ + I₅ = 0 ;

–I₃ – I₅ + I₆ = 0 .

Визначаємо сили струмів у розгалуженнях за допомогою законів Ома для ділянок кола з е.р.с. і без е.р.с.:

; ₀ = 0 ; – провідність ділянки, См.

З урахуванням провідностей одержимо:

I₁ = (–₁ + Е₁)g₁ ;

I₂ = (–₂ + Е₂)g₂ ;

I₃ = (–₃ + Е₃)g₃ ;

I₄ = (₁ – ₂)g₄ ;

I₅ = (₂ – ₃)g₅ ;

I₆ = (₃ – ₁)g₆ ,

де ₁ , ₂ , ₃ – потенціали вузлів 1, 2, 3, В.

Отримані вирази сил струмів підставляємо в рівняння, складені за 1-м законом Кірхгофа:

₁ g₁ – Е₁ g₁ + ₁ g₄ – ₂ g₄ + ₁ g₆ – ₃ g₆ = 0 ;

₂ g₂ – Е₂ g₂ + ₂ g₄ – ₁ g₄ + ₂ g₅ – ₃ g₅ = 0 ;

₃ g₃ – Е₃ g₃ + ₃ g₅ – ₂ g₅ + ₃ g₆ – ₁ g₆ = 0 .

Після перетворення одержимо:

(g₁ + g₄ + g₆)₁ – ₂ g₄ – ₃ g₆ = Е₁ g₁ ;

–₁ g₄ + (g₂ + g₄ + g₅)₂ – ₃ g₅ = Е₂ g₂ ;

–₁ g₆ – ₂ g₅ + (g₃ + g₅ + g₆)₃ = Е₃ g₃ .

Уводимо позначення:

g₁ + g₄ + g₆ = g₁₁ ; g₄ = g₁₂ ; g₄ = g₂₁ ;

g₂ + g₄ + g₅ = g₂₂ ; g₅ = g₂₃ ; g₅ = g₃₂ ;

g₃ + g₅ + g₆ = g₃₃ ; g₆ = g₁₃ ; g₆ = g₃₁ ;

;

;

,

де g₁₁ , g₂₂ , g₃₃ – суми провідностей розгалужень,

приєднаних відповідно до вузлів 1, 2 і 3, См;

g₁₂ = g₂₁ , g₂₃ = g₃₂ , g₁₃ = g₃₁ – суми провідностей розгалужень

відповідно між вузлами 1 і 2, 2 і 3, 1 і 3, См;

, , – алгебраїчна сума добутків е.р.с. джерел

на відповідні провідності розгалужень,

приєднаних до розглядаємих вузлів

(добуток Еg береться зі знаком «+»,

якщо е.р.с. спрямована до вузла;

зі знаком «–», якщо е.р.с. спрямована від вузла), А.

З урахуванням уведених позначень одержимо:

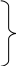; (2.6)

; (2.7)

. (2.8)

Приклад 2.2

Використовуючи значення параметрів у прикладі 2.1, знайти сили струмів у розгалуженнях методом вузлових потенціалів.

Рішення.

Використовуємо рівняння (2.6), (2.7), (2.8) і визначаємо провідності і добутки е.р.с. на провідності:

g₁ = 1,67 См ; g₄ = 0,5 См ; g₁₁ = 3,17 См ; ;

g₂ = 0,83 См ; g₅ = 0,5 См ; g₂₂ = 1,83 См ; ;

g₃ = 0,63 См ; g₆ = 1,0 См ; g₃₃ = 2,13 См ; .

Після підстановки знайдених значень в отриману систему рівнянь отримаємо:

3,17₁ – 0,5₂ – 1₃ = 16,7 ;

–0,5₁ +1,83₂ – 0,5₃ = 49,8 ;

–1₁ – 0,5₂ +2,13₃ = 25,2 .

Вирішуємо отриману систему рівнянь за допомогою визначників третього порядку. Знаходимо визначник системи:

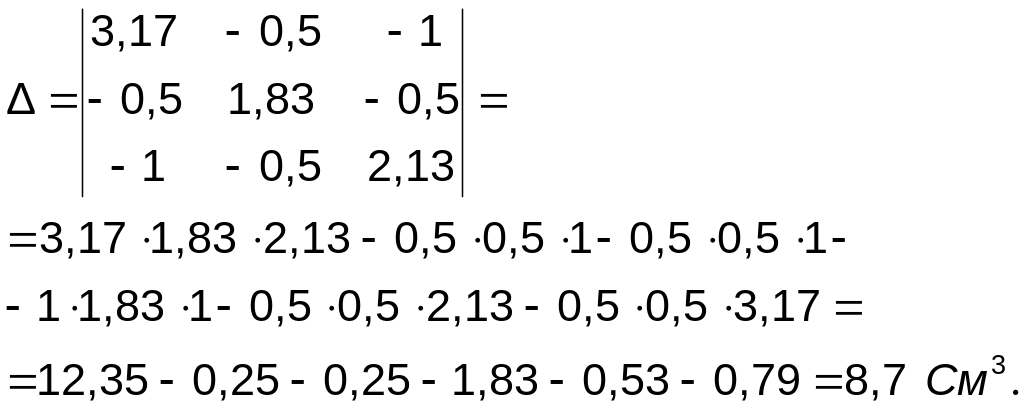
Знаходимо доповнення визначника:

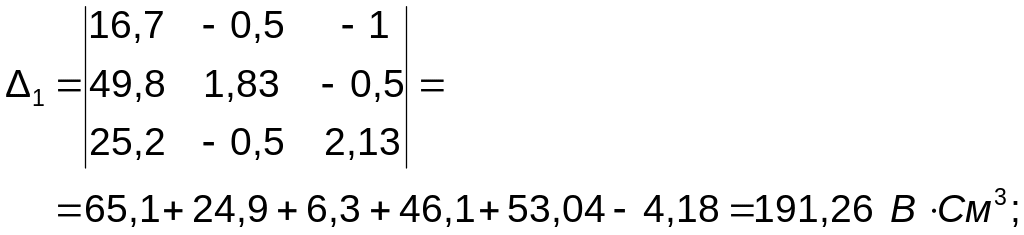
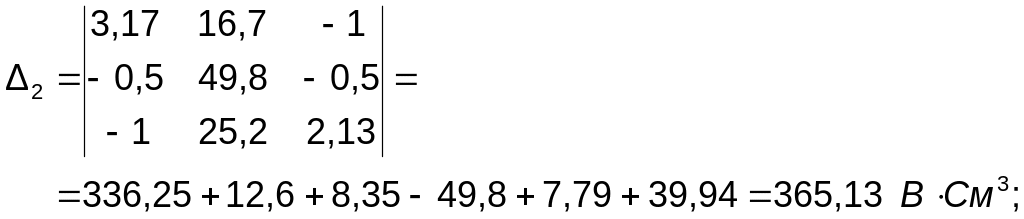
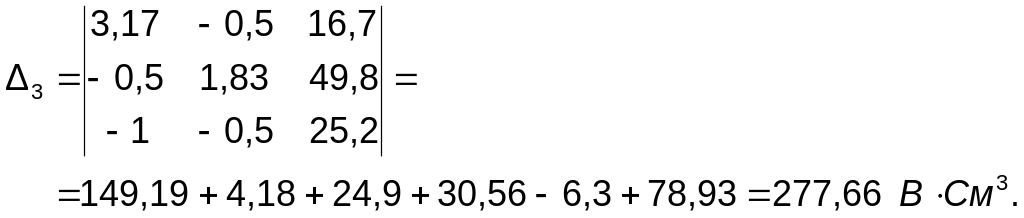
Визначаємо потенціали вузлів 1, 2 і 3:

Визначаємо сили струмів у розгалуженнях схеми електричного кола: